Строительство перпендикуляра к плоскости является одной из основных задач в начертательной геометрии. Перпендикуляр - это линия или отрезок, который образует прямой угол с плоскостью. Эта задача может быть полезна во многих областях, таких как архитектура, инженерия и дизайн. В данной статье мы представим несколько способов решения этой задачи.
Первый способ состоит в использовании угломерного прибора. Угломерный прибор - это инструмент, который позволяет измерять углы. Для строительства перпендикуляра с помощью угломерного прибора, необходимо измерить любой угол между пересекающей плоскостью и осью, проходящей через заданную точку. Затем необходимо построить угол, равный полученному измерению, отложить его от заданной точки и полученная линия будет перпендикулярной к плоскости.
Второй способ основан на использовании перпендикулярных линий. Для этого необходимо провести две линии на плоскости, образующие прямой угол. Затем, используя циркуль и линейку, необходимо построить линию, параллельную одной из перпендикулярных линий, отложив расстояние, равное расстоянию между двумя линиями на плоскости. Полученная линия будет перпендикулярной к плоскости и проходить через заданную точку.
Третий способ использует пересечение плоскости с перпендикулярной прямой. Для этого необходимо построить проекцию плоскости на плоскость перпендикулярной прямой. Затем необходимо провести прямую, пересекающую плоскость в точке, а затем перпендикулярно проектировать эту точку на плоскость перпендикулярной прямой. Полученная линия будет перпендикулярной к плоскости и проходить через заданную точку.
Определение понятия "перпендикуляр к плоскости"

Перпендикуляр к плоскости может быть построен с использованием метода точки и прямой, а именно: проведением прямой, перпендикулярной к данной плоскости, через заданную точку вне этой плоскости.
Для построения перпендикуляра к плоскости необходимо выбрать заданную точку вне плоскости и провести прямую, которая будет пересекать эту плоскость под прямым углом.
Пример:
Дана плоскость ABCD и точка P вне плоскости. Чтобы построить перпендикуляр к плоскости, проведем прямую, которая пересечет плоскость под прямым углом. В результате получим перпендикулярную прямую, которая будет проходить через точку P и пересекать плоскость ABCD под прямым углом.
Особенности построения перпендикуляра к плоскости
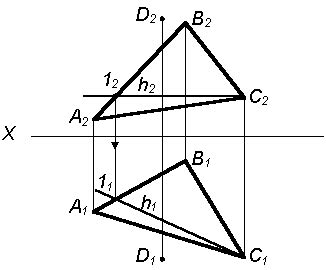
Для построения перпендикуляра к плоскости необходимо выполнить следующие шаги:
- Выберите заданную точку, через которую будет проходить перпендикуляр.
- Прокладывайте линию, проходящую через эту точку и перпендикулярно плоскости.
Однако, построение перпендикуляра к плоскости может иметь некоторые особенности:
| Особенность | Описание |
|---|---|
| Выбор точки | Выбранная точка должна находиться вне плоскости. В противном случае, линия, проведенная через точку, будет лежать в плоскости, а не быть перпендикулярной к ней. |
| Определение плоскости | Для построения перпендикуляра к плоскости необходимо точно определить данную плоскость. Это может потребовать дополнительных данных, таких как еще одна точка или направляющий вектор плоскости. |
| Тип плоскости | Существуют различные типы плоскостей, такие как плоскость параллельна плоскости заданной точки или плоскость, проходящая через заданную точку. При построении перпендикуляра к определенной плоскости нужно учитывать ее тип и свойства. |
Важно помнить, что построение перпендикуляра к плоскости требует точной геометрической прокладки и учета особенностей задачи.
Алгоритм построения перпендикуляра к плоскости
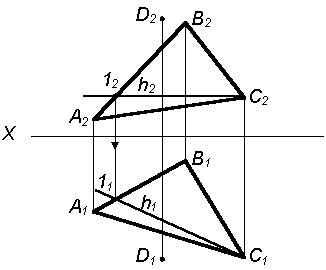
- Найдите точку на плоскости, через которую должен проходить перпендикуляр. Обозначим эту точку как А.
- Найдите прямую линию на плоскости, к которой должен быть перпендикуляр. Обозначим эту линию как BC.
- Постройте прямую линию, проходящую через точку А и перпендикулярную линии BC. Для этого найдите середину отрезка BC и построить прямую линию, перпендикулярную BC и проходящую через середину.
Таким образом, используя данный алгоритм, вы можете построить перпендикулярную плоскость линию, проходящую через заданную точку и перпендикулярную данной линии на плоскости.
Примеры построения перпендикуляра к плоскости
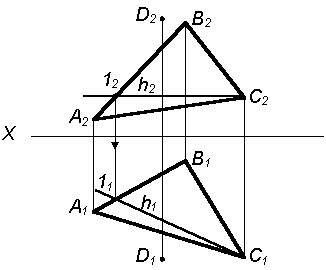
Существует несколько способов построения перпендикуляра к плоскости. Ниже приведены два примера:
Пример 1:
- Начертите плоскость, к которой нужно построить перпендикуляр.
- Выберите точку на этой плоскости, через которую должен проходить перпендикуляр, и обозначьте ее как точку А.
- Постройте от точки А отрезок, перпендикулярный плоскости, с помощью острого угла в компасе.
- Обозначьте конец отрезка как точку В. Теперь, отрезок АВ будет перпендикулярным к плоскости.
Пример 2:
- Начертите плоскость, к которой нужно построить перпендикуляр.
- Выберите точку на этой плоскости, через которую должен проходить перпендикуляр, и обозначьте ее как точку А.
- Начертите две прямые, проходящие через точку А, но не лежащие в плоскости, и обозначьте их как прямые АВ и АС.
- Найдите точку пересечения прямых АВ и АС и обозначьте ее как точку D.
- Постройте отрезок от точки А до точки D. Этот отрезок будет перпендикулярным к плоскости.
Это лишь некоторые из возможных способов построения перпендикуляра к плоскости. Вы можете использовать любой другой метод в зависимости от конкретной ситуации.