Построение плоскости для двух векторов является важной задачей в линейной алгебре и геометрии. Это позволяет наглядно представить линейные комбинации данных векторов и описать пространство, которое они порождают. В данном подробном руководстве мы рассмотрим этот процесс шаг за шагом.
Первым шагом в построении плоскости для двух векторов является выбор этих векторов. Векторы могут быть представлены в виде списка координат или графически на координатной плоскости. Для удобства, обозначим эти векторы как A и B.
Далее, мы можем найти два неколлинеарных вектора, которые ортогональны векторам A и B. Эти векторы называются нормальными векторами и будут определять плоскость. Они могут быть найдены с помощью векторного произведения (cross-product) или путем решения системы уравнений, зависящих от координат векторов A и B.
Теперь, когда у нас есть два нормальных вектора, мы можем установить точку плоскости, которая будет служить началом координат для построения плоскости. Зная координаты этой точки, а также нормальные векторы, мы можем записать уравнение плоскости в виде Ax + By + Cz + D = 0, где A, B, C и D - коэффициенты.
Окончательным шагом в построении плоскости для двух векторов является визуализация самой плоскости. Это можно сделать с помощью графических программ или отобразить на координатной плоскости, используя уравнение плоскости и представив каждую координату как ось на графике.
Теперь, имея полное понимание процесса, вы можете успешно построить плоскость для двух векторов. Это поможет вам лучше визуализировать пространство, которое они образуют, и решать разнообразные задачи, связанные с линейной алгеброй и геометрией.
Как построить плоскость для двух векторов: необходимое оборудование
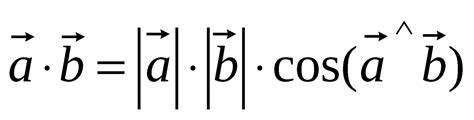
Для построения плоскости, проходящей через два заданных вектора, потребуется несколько инструментов и материалов:
1. Линейка - для измерения длин векторов и прямых на плоскости.
2. Карандаш - для обозначения точек и отрезков на плоскости.
3. Маркер или фломастер - для выделения главных осей и векторов на плоскости.
4. Угольник - для построения перпендикуляров к векторам и измерения углов.
5. Бумага - предпочтительно использовать графическую или координатную бумагу, чтобы облегчить построение и применение сетки.
6. Компас - для построения окружностей, если это необходимо в задаче.
7. Ровная поверхность - для проведения аккуратных линий и точек, рекомендуется использовать подложку из плотного материала, такого как картон или дерево.
8. Точный нож или ножницы - для вырезания фигур, если это необходимо для построения.
9. Стержни или нитки - если необходимо проводить перпендикуляры с использованием метода натянутой нитки.
Используя все указанные инструменты и материалы вместе, вы сможете точно и графически построить плоскость для двух заданных векторов и провести необходимые измерения и анализы.
Инструменты для построения плоскости
Для построения плоскости, проходящей через два заданных вектора, требуется использование нескольких инструментов и техник. Вот некоторые из них:
1. Начните с определения начальной точки плоскости. Это может быть любая точка в трехмерном пространстве. Вы можете выбрать точку, через которую должна проходить плоскость.
2. Векторы, через которые должна проходить плоскость, являются ее направляющими векторами. Используйте их для определения направления плоскости. Векторное произведение этих векторов даст вектор, перпендикулярный плоскости.
3. Проекция вектора на плоскость может быть использована для создания дополнительных вспомогательных векторов. Для этого вычтите проекцию векторов на перпендикулярный плоскости вектор из исходных векторов.
4. Используйте найденные вспомогательные векторы и начальную точку плоскости, чтобы построить плоскость. Положите начальную точку и направляющие векторы на координатной плоскости трехмерного пространства и прочертите по ним плоскость.
При использовании этих инструментов и техник вы сможете построить плоскость, проходящую через два заданных вектора в трехмерном пространстве. В физике и геометрии плоскости часто используются для решения различных задач и моделирования трехмерных объектов.
Материалы, необходимые для построения плоскости
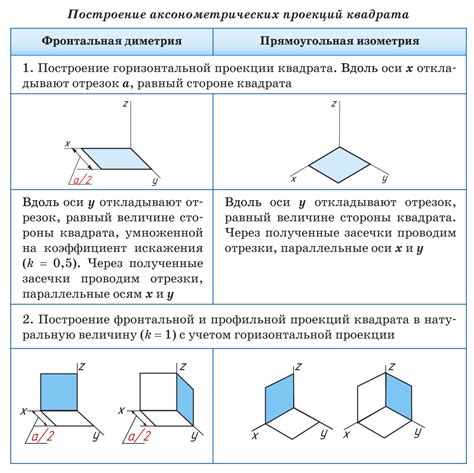
Для построения плоскости, проходящей через два заданных вектора, вам понадобятся следующие материалы:
1. Лист бумаги или доска - для нанесения рисунка и проведения линий.
2. Линейка - для проведения прямых и измерения отрезков.
3. Графитовый карандаш или ручка - для нанесения линий и обозначения векторов.
4. Маркеры или цветные карандаши - для выделения плоскости и векторов на рисунке.
5. Угольник - для построения прямых под определенным углом и проверки перпендикулярности.
6. Стерка - для исправления ошибок и удаления ненужных линий.
Убедитесь, что у вас есть все необходимые материалы перед началом работы. Они помогут вам точно и наглядно построить плоскость, соответствующую заданным векторам.
Как построить плоскость для двух векторов: шаги выполнения
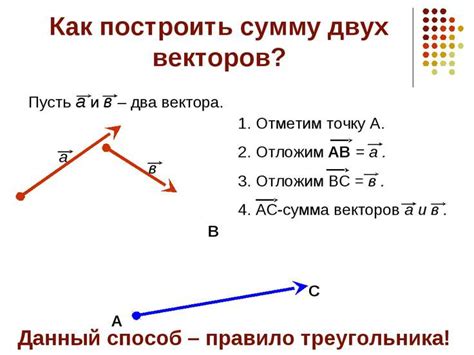
Построение плоскости для двух векторов требует выполнения нескольких шагов. Вот подробное руководство по этому процессу:
- Выберите два неколлинеарных вектора. Убедитесь, что они не являются параллельными и не лежат на одной прямой. Это важно для создания плоскости.
- Найдите векторное произведение (кросс-произведение) выбранных векторов. Векторное произведение создаст новый вектор, перпендикулярный обоим векторам и определяющий направление плоскости.
- Найдите координаты точки, через которую должна проходить плоскость. Вы можете использовать вершину координатной системы или выбрать другую точку, находящуюся на плоскости.
- Используя найденные векторы и координаты точки, записывайте уравнение плоскости в виде Ax + By + Cz + D = 0, где (x, y, z) - координаты любой точки на плоскости, а A, B, C и D - коэффициенты уравнения плоскости.
- Постройте график найденной плоскости, используя уравнение и координатную систему. Вы можете использовать программы для работы с трехмерной графикой или рисовать плоскость вручную на бумаге, отмечая координаты точек.
Следуя этим шагам, вы сможете построить плоскость для двух векторов и визуализировать ее графически. Этот процесс поможет вам лучше понять взаимное влияние векторов и создать базу для более сложных графических вычислений и анализа.
Подготовка основания для плоскости
Прежде чем приступить к построению плоскости для двух векторов, необходимо подготовить основание, на котором будет проводиться само построение. Основание может быть представлено в виде горизонтальной плоскости или листа бумаги.
При выборе основания важно учесть его размеры. Основание должно быть достаточно большим, чтобы вместить оба вектора, а также иметь свободное пространство вокруг них. Это позволит удобно работать с векторами и избежать пересечения линий построения.
Одним из распространенных подходов к созданию основания является использование листа бумаги формата А4 или большего формата. Такой подход позволяет удобно разместить векторы на поверхности и провести все необходимые линии.
- Возьмите лист бумаги выбранного формата и положите его на ровную поверхность (например, на стол).
- Расправьте лист и убедитесь, что он не имеет помятостей или складок.
- При помощи линейки и карандаша проведите две перпендикулярные линии на листе, чтобы создать координатную плоскость. Одна линия будет служить осью x, а другая - осью y.
- Обозначьте начало координат, где линии пересекаются. Для лучшей визуализации можно отметить начало координат кружком или точкой.
После того, как основание подготовлено, можно приступать к построению плоскости для двух векторов. Основание в виде координатной плоскости поможет визуально представить положение и направление векторов, а также провести все необходимые вычисления и построения.