Построение полинома Жегалкина является важным инструментом в теории логических функций. Полином Жегалкина представляет собой альтернативную форму записи булевой функции, которая удобна для многих приложений, включая схемотехнику, алгоритмы поиска, криптографию и другие.
Основная идея состоит в том, чтобы представить логическую функцию в виде полинома, где каждое слагаемое соответствует конъюнкции или дизъюнкции переменных в функции. Вектор значений, полученный из таблицы истинности функции, является ключевым элементом в построении полинома Жегалкина.
В данной статье мы рассмотрим основные шаги построения полинома Жегалкина на примерах. Мы начнем с анализа вектора значений и определения переменных. Затем мы рассмотрим алгоритм построения полинома Жегалкина и его применение на практике. В завершение статьи мы рассмотрим некоторые дополнительные сведения и подведем итоги.
Что такое полином Жегалкина?

Полином Жегалкина представляет собой формулу, состоящую из суммы произведений переменных и их отрицаний. Каждое слагаемое в полиноме Жегалкина соответствует одному значению таблицы истинности булевой функции. Таким образом, полином Жегалкина компактно описывает все значиения булевой функции в виде алгебраического выражения.
Полином Жегалкина имеет следующую форму:
- Возможные переменные принимают значения 0 или 1. Например, полином Жегалкина для двух переменных (x1, x2) будет выглядеть следующим образом: f(x1, x2) = a + b*x1 + c*x2 + d*x1*x2, где a, b, c, d - коэффициенты полинома Жегалкина.
- Каждая переменная может быть отрицательной или положительной.
- Полином Жегалкина может включать слагаемые с различными степенями переменных.
Полином Жегалкина является мощным инструментом для анализа и синтеза булевых функций. Он позволяет упростить выражения и решать различные задачи, связанные с булевым алгеброй, комбинаторикой и схемотехникой. Кроме того, полином Жегалкина играет важную роль в криптографии и теории кодирования.
Определение и основные понятия
При изучении полиномов Жегалкина важно понимать некоторые основные понятия и определения.
Полином Жегалкина - это полином, представляющий функцию в виде суммы произведений переменных, принимающих значения 0 или 1, с коэффициентами 0 или 1. Каждое произведение соответствует конъюнкции переменных, а сумма произведений - дизъюнкции конъюнкций.
Вектор значений - это последовательность значений функции для различных наборов переменных. Вектор значений может быть записан в виде битовой строки, где каждый бит соответствует значению функции для соответствующего набора переменных.
Мономы - это произведения переменных, в которых каждая переменная может принимать значение 0 или 1. Каждый моном соответствует набору переменных, для которых произведение равно 1. Например, моном x1x2 соответствует набору переменных [1, 1], а моном x1x2' соответствует набору переменных [1, 0].
Обобщенный моном - это моном, в котором к каждой переменной может быть применен инвертор. Обобщенный моном соответствует набору переменных, каждая из которых может быть инвертирована или не инвертирована.
Коэффициенты полинома Жегалкина являются знаками перед каждым мономом в полиноме. Знак "+" перед мономом означает положительный коэффициент, а знак "-" перед мономом означает отрицательный коэффициент.
Минимальный полином Жегалкина - это полином Жегалкина, в котором отсутствуют ненужные слагаемые и коэффициенты. Минимальный полином Жегалкина является наиболее простым и удобным для анализа.
Определение и понимание этих основных понятий позволяет использовать полиномы Жегалкина в различных областях, таких как логическое программирование, цифровая электроника и криптография.
Понимание работы полинома Жегалкина

Полином Жегалкина может быть использован для упрощения и анализа булевых функций, а также для построения электронных схем и разработки программного обеспечения. Он основывается на теории булевой алгебры и имеет широкий спектр применений в компьютерной науке, телекоммуникациях и криптографии.
Для построения полинома Жегалкина по вектору значений необходимо выполнить ряд шагов. Сначала определить количество переменных в булевой функции. Затем составить таблицу истинности, в которой указать все возможные комбинации значений переменных и соответствующие им значения функции.
Далее можно использовать метод Квайна-МакКласки для упрощения таблицы истинности и удаления избыточных строк. Затем составляется система линейных уравнений, в которой каждому моному присваивается свой коэффициент. В результате решения этой системы получается полином Жегалкина.
Полином Жегалкина представляет функцию в виде комбинации логических операций и переменных. Он позволяет удобно анализировать функции и проводить операции с ними, такие как упрощение, дифференцирование и интегрирование.
Полином Жегалкина является мощным инструментом в области логической алгебры и имеет широкое применение в различных отраслях. Понимание его работы позволяет разрабатывать более эффективные алгоритмы и решать сложные задачи, связанные с обработкой информации и управлением системами.
Примеры использования полинома Жегалкина

Примеры использования полинома Жегалкина включают:
- Анализ функциональных зависимостей: полином Жегалкина может использоваться для определения, какие переменные влияют на результат булевой функции. Это позволяет идентифицировать ключевые факторы, которые влияют на функцию и понять ее поведение.
- Оптимизация логических схем: полином Жегалкина может быть использован для сокращения количества логических элементов, необходимых для реализации булевой функции. Путем анализа полинома Жегалкина можно выделить общие части и использовать их для построения сокращенной схемы.
- Криптография: полином Жегалкина может быть использован для построения криптографических алгоритмов, таких как шифрование и кодирование. За счет своей универсальности и эффективности, полином Жегалкина является важным инструментом в области безопасности информации.
Применение полинома Жегалкина позволяет более эффективно анализировать и понимать булевые функции, что делает его неотъемлемым инструментом в различных областях науки и техники.
Пример преобразования вектора значений в полином Жегалкина
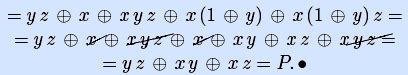
Для примера возьмем вектор значений функции f = [0, 1, 1, 0]. Этот вектор содержит результаты вычисления функции на всех возможных комбинациях входных значений.
Для начала, нам нужно преобразовать вектор значений в таблицу истинности:
| Входы | Выходы |
|---|---|
| 0 | 0 |
| 0 | 1 |
| 1 | 1 |
| 1 | 0 |
Затем мы можем использовать таблицу истинности для построения полинома Жегалкина. Для этого мы можем записать логические выражения, которые получаются, когда наблюдается 1 на выходе функции.
В нашем примере, получаем следующие выражения:
f(0, 0) = 0
f(0, 1) = 1
f(1, 0) = 1
f(1, 1) = 0
Теперь мы можем записать полином Жегалкина, используя переменные a и b:
f = ab + a + b
В этом примере мы видим, что полином Жегалкина позволяет нам представить функцию f с помощью всего трех членов, включая линейный член a и b, а также один квадратичный член ab.