В современном мире объем данных, с которыми мы работаем, растет с каждым днем. Изучение и анализ этих данных становится все более важным для принятия обоснованных решений во многих областях жизни, от бизнеса до науки.
Одним из инструментов, позволяющих получить полезные инсайты из многомерных данных, является проекция Фишера. Это метод, разработанный Рональдом Аилмером Фишером в 1936 году, который позволяет снизить размерность многомерных данных и визуализировать их в двумерном пространстве.
Проекция Фишера может быть полезна при анализе данных различных типов: от экономических показателей до генетических данных. Она позволяет нам увидеть основные закономерности и структуру данных, которую сложно обнаружить в исходном пространстве.
В данной статье мы рассмотрим основные этапы построения проекции Фишера: от подготовки данных до интерпретации полученных результатов. Мы расскажем о методах снижения размерности, основных принципах работы проекции Фишера, а также о том, как правильно интерпретировать полученные результаты и использовать их для принятия обоснованных решений.
Определение метода проекции Фишера
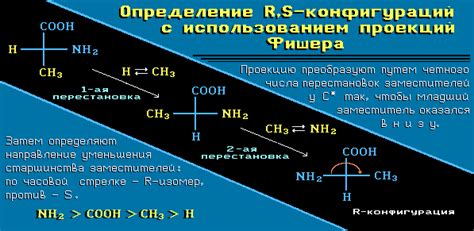
Процесс построения проекции Фишера состоит из следующих шагов:
- Вычислить среднее значение каждого признака для каждого класса.
- Вычислить матрицу разброса между классами (межклассовая матрица разброса).
- Вычислить матрицу разброса внутри классов (внутриклассовая матрица разброса).
- Вычислить обратную к внутриклассовой матрице разброса.
- Умножить матрицу разброса между классами на обратную матрицу разброса внутри классов.
- Рассчитать собственные значения и собственные векторы полученной матрицы.
- Выбрать проекцию, соответствующую k самым большим собственным значениям.
Итак, метод проекции Фишера позволяет нам выбрать новые признаки, которые наилучшим образом отделяют классы в исходных данных. Это может быть полезно при визуализации данных, а также может помочь в построении моделей машинного обучения и классификации.
Преимущества и области применения

- Улучшение качества классификации: Проекция Фишера позволяет учесть все информативные признаки и убрать ненужные, что помогает увеличить точность классификации.
- Снижение размерности данных: Метод Фишера позволяет снизить размерность данных, сохраняя при этом большую часть информации, что делает его особенно полезным при работе с большими наборами данных.
- Построение визуализаций: Проекция Фишера может быть использована для построения двумерных или трехмерных визуализаций данных, что помогает наглядно представить распределение объектов и выявить взаимосвязи между признаками.
- Автоматизация процесса выбора признаков: Метод Фишера позволяет автоматически отбирать наиболее значимые признаки, исключая неинформативные. Это упрощает анализ данных и повышает эффективность работы.
Проекция Фишера находит применение в различных областях:
- Машинное обучение: Проекция Фишера используется для решения задач классификации и кластеризации, а также для снижения размерности данных перед применением методов машинного обучения.
- Биоинформатика: Метод Фишера может быть применен для анализа геномных данных, поиска генов-маркеров и классификации образцов.
- Финансовая аналитика: Проекция Фишера может быть использована для анализа финансовых данных, прогнозирования рыночных трендов и построения портфелей инвестиций.
- Изображение и обработка сигналов: Метод Фишера может быть применен для анализа и классификации изображений, а также для снижения размерности и улучшения качества обработки сигналов.
В целом, проекция Фишера является важным инструментом анализа данных, который может быть применен во многих областях и помогает улучшить качество классификации, снизить размерность данных и автоматизировать процесс выбора признаков.
Подготовка данных для проекции Фишера
Перед тем как приступить к построению проекции Фишера, необходимо подготовить исходные данные. Важными этапами подготовки данных являются:
- Выбор признаков:
Начните с анализа доступных признаков и определите, какие из них являются наиболее информативными для вашей задачи. Удалите из рассмотрения признаки, которые не несут значимой информации или сильно коррелируют с другими признаками. Не забудьте учесть доменные знания и особенности вашего набора данных при выборе признаков.
- Обработка пропущенных данных:
Если ваш набор данных содержит пропущенные значения, необходимо решить, как с ними поступить. Вы можете удалить строки или столбцы с пропущенными значениями, заполнить их средними или медианными значениями, или использовать более сложные алгоритмы заполнения пропусков на основе моделей машинного обучения.
- Нормализация признаков:
Чтобы избежать проблем с масштабом признаков, рекомендуется нормализовать их перед построением проекции Фишера. Это можно сделать путем преобразования значений признаков к диапазону от 0 до 1 или использования стандартного нормального распределения.
- Разделение данных на классы:
Если у вас есть информация о принадлежности объектов к определенным классам, разделите данные на соответствующие классы. Это позволит вам использовать информацию о классе при построении проекции Фишера.
Подготовка данных – важный шаг перед построением проекции Фишера и может существенно повлиять на результаты анализа. Исходя из особенностей вашего набора данных и цели исследования, примените нужные методы по выбору признаков, обработке пропусков, нормализации и разделению данных.
Выбор источника данных
Один из возможных источников данных - это открытые и доступные публичные базы данных, которые содержат информацию о различных сферах деятельности. Такие базы данных могут быть предоставлены государственными организациями, исследовательскими учреждениями или коммерческими организациями.
Также можно использовать собственные данные, полученные в результате исследования или сбора информации. Это может быть опрос, эксперимент, анализ уже существующих данных и т.д. Важно учесть, что при использовании собственных данных необходимо обеспечить их надежность и актуальность.
При выборе источника данных следует обратить внимание на следующие критерии:
- Надежность: источник данных должен быть достоверным и обладать высокой степенью достоверности информации.
- Актуальность: данные должны быть актуальными и соответствовать требуемому временному интервалу.
- Объем: источник данных должен содержать достаточное количество информации для проведения анализа.
- Доступность: данные должны быть доступными для использования и обладать необходимыми правами на доступ.
Важно также проверить данные на наличие выбросов, пропусков и других ошибок, которые могут искажать результаты анализа.
Выбор источника данных является важным этапом перед построением проекции Фишера. Правильный выбор позволит получить достоверные и релевантные результаты анализа.
Предварительная обработка данных
Перед тем, как приступить к построению проекции Фишера, необходимо выполнить предварительную обработку данных. Этот этап включает в себя несколько шагов, которые помогут вам подготовить данные для анализа:
1. Импорт данных: Сначала необходимо импортировать данные, которые вы хотите анализировать, в программное обеспечение, которое вы планируете использовать для построения проекции Фишера. Обычно данные представлены в виде таблицы, где каждая строка соответствует отдельной наблюдаемой единице, а каждый столбец - переменной, которую вы хотите включить в анализ.
2. Удаление выбросов: Выбросы могут исказить результаты анализа и повлиять на точность построения проекции Фишера. Поэтому рекомендуется удалить выбросы из данных. Для этого можно использовать различные статистические методы, такие как удаление значений, находящихся за пределами трех стандартных отклонений от среднего значения, или метод квантилей.
3. Обработка пропущенных значений: Если ваши данные содержат пропущенные значения, то необходимо решить, как их обработать. Вы можете удалить строки или столбцы с пропущенными значениями, заполнить их средними или медианными значениями, или использовать другие методы для заполнения пропусков.
4. Масштабирование данных: Важным шагом в предварительной обработке данных является масштабирование переменных. Если переменные имеют различные единицы измерения или значительно отличаются по масштабу, то это может повлиять на построение проекции Фишера. Чтобы избежать этого, имеет смысл нормализовать переменные, например, путем приведения их к среднему значению 0 и стандартному отклонению 1.
5. Выбор релевантных переменных: Не все переменные могут быть полезны для построения проекции Фишера. Поэтому рекомендуется провести анализ и определить, какие переменные будут наиболее информативны для вашей конкретной задачи. Для этого можно использовать корреляционный анализ или другие статистические методы.
| Шаг | Описание |
|---|---|
| 1 | Импорт данных |
| 2 | Удаление выбросов |
| 3 | Обработка пропущенных значений |
| 4 | Масштабирование данных |
| 5 | Выбор релевантных переменных |
Реализация проекции Фишера
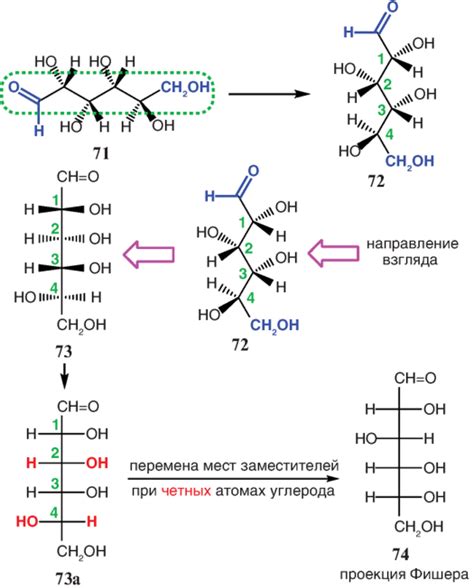
Для реализации проекции Фишера необходимо выполнить следующие шаги:
- Получить данные: подготовьте набор данных, где каждому объекту будет соответствовать вектор признаков и метка класса.
- Вычислить средние значения классов: для каждого класса вычислите средний вектор признаков.
- Вычислить внутриклассовую матрицу рассеяния: для каждого класса вычислите матрицу рассеяния и сложите их воедино.
- Вычислить межклассовую матрицу рассеяния: вычислите сумму матрицы рассеяния каждого класса с учетом количества объектов в каждом классе.
- Вычислить собственные значения и собственные векторы матрицы Фишера: решите уравнение \(\mathbf{S}_B \mathbf{w} = \lambda \mathbf{S}_W \mathbf{w}\), где \(\mathbf{S}_B\) – межклассовая матрица рассеяния, \(\mathbf{S}_W\) – внутриклассовая матрица рассеяния.
- Отобрать признаки: отсортируйте собственные значения в убывающем порядке и выберите первые \(k\) собственных векторов, соответствующих наибольшим собственным значениям, где \(k\) – новая размерность пространства признаков.
- Проецировать данные: умножьте исходные данные на матрицу собственных векторов, чтобы получить новые данные с уменьшенной размерностью.
Для более наглядного представления результатов проекции Фишера, можно визуализировать исходные и преобразованные данные, используя диаграммы рассеяния.
| Шаг | Наименование | Описание |
|---|---|---|
| 1 | Получить данные | Подготовьте набор данных, где каждому объекту будет соответствовать вектор признаков и метка класса. |
| 2 | Вычислить средние значения классов | Для каждого класса вычислите средний вектор признаков. |
| 3 | Вычислить внутриклассовую матрицу рассеяния | Для каждого класса вычислите матрицу рассеяния и сложите их воедино. |
| 4 | Вычислить межклассовую матрицу рассеяния | Вычислите сумму матрицы рассеяния каждого класса с учетом количества объектов в каждом классе. |
| 5 | Вычислить собственные значения и собственные векторы матрицы Фишера | Решите уравнение \(\mathbf{S}_B \mathbf{w} = \lambda \mathbf{S}_W \mathbf{w}\), где \(\mathbf{S}_B\) – межклассовая матрица рассеяния, \(\mathbf{S}_W\) – внутриклассовая матрица рассеяния. |
| 6 | Отобрать признаки | Отсортируйте собственные значения в убывающем порядке и выберите первые \(k\) собственных векторов, соответствующих наибольшим собственным значениям, где \(k\) – новая размерность пространства признаков. |
| 7 | Проецировать данные | Умножьте исходные данные на матрицу собственных векторов, чтобы получить новые данные с уменьшенной размерностью. |
Реализация проекции Фишера позволяет снизить размерность данных, сохраняя при этом наиболее разделяющие классы признаки. Этот метод является мощным инструментом анализа данных и может быть использован для решения различных задач классификации и кластеризации.
Выбор числа компонент
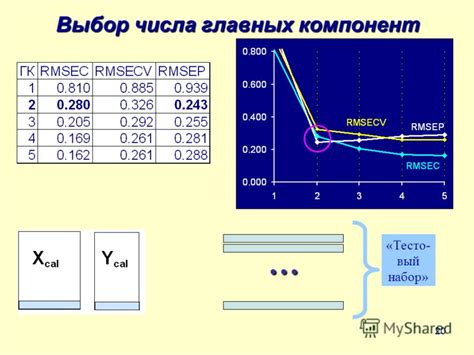
Для выбора числа компонент можно использовать различные подходы. Один из них - анализ доли объясненной дисперсии. В этом случае, мы анализируем, какое количество компонент объясняет большую часть дисперсии в данных. Обычно выбирают достаточное число компонент, которое объясняет около 80-90% дисперсии.
Другой подход - анализ собственных значений. Собственные значения компонент являются мерой их вклада в общую дисперсию данных. При анализе собственных значений, мы выбираем те компоненты, у которых собственные значения существенно отличаются от нуля. Чем больше собственные значения, тем больший вклад вносит компонента в описание данных.
Кроме того, можно использовать метод кумулятивной суммы собственных значений. В этом случае, мы суммируем собственные значения компонент, начиная с наибольшего, и выбираем те компоненты, которые объясняют определенный процент общей дисперсии, например, 90%. Этот метод позволяет выбрать оптимальное число компонент, которые вносят основной вклад в описание данных.
Задание параметров проекции
Ключевым параметром проекции Фишера является число компонент. Оно определяет количество основных компонент, которые будут использованы для проекции данных. Выбор оптимального числа компонент зависит от цели анализа и структуры данных. Если число компонент слишком мало, проекция может быть неинформативной и не отобразить важные характеристики данных. Если число компонент слишком велико, проекция может содержать избыточную информацию и быть сложной для интерпретации.
Другим важным параметром является метод определения собственных значений. Проекция Фишера может использовать различные методы, такие как метод собственных значений или метод собственных векторов. Выбор оптимального метода зависит от типа данных и его структуры.
Наконец, необходимо задать параметр нормализации данных. Это может быть центрирование и стандартизация данных, чтобы обеспечить их сравнимость и избежать влияния различий в шкалах измерений.
Правильный выбор параметров проекции Фишера позволит получить удобную и информативную визуализацию данных, которая поможет в их дальнейшем анализе и исследовании.