Проекции прямых на плоскость играют важную роль в геометрии и инженерных расчетах. Этот метод позволяет нам представить трехмерные объекты в двумерном пространстве, что делает их легче визуализируемыми и позволяет быстро решать сложные задачи.
В этом руководстве я подробно расскажу о построении проекции прямой на плоскость. Мы рассмотрим различные методы, которые могут использоваться для этой цели. Вы узнаете, как правильно определить положение прямой и плоскости в пространстве, а также как найти проекцию с помощью формул и графических методов.
Знание построения проекции прямой на плоскость является важной составляющей для работы в области графики, архитектуры и инженерии. Благодаря этому навыку вы сможете быстро решать задачи, связанные с определением положения объектов в пространстве и их визуализацией на плоскости.
Что такое проекция прямой на плоскость?

Проекции используются в различных областях, включая графическое моделирование, инженерное проектирование и архитектуру. Они позволяют строить более точные и реалистичные модели, а также решать различные задачи, связанные с геометрией.
Одним из примеров применения проекций прямых на плоскости является построение чертежей зданий и сооружений. С помощью проекций можно получить более точное представление о форме и размерах объектов, что облегчает их дальнейшую конструкцию и планирование.
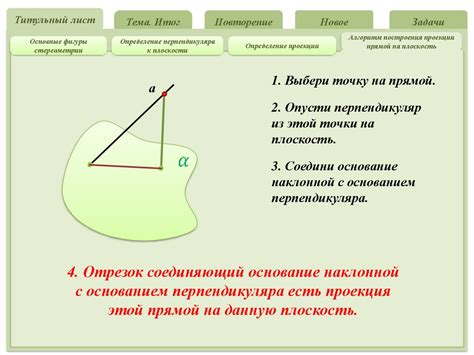
Для построения проекции прямой на плоскость необходимо знать ее направление и точку пересечения с плоскостью проекций. Эти данные позволяют нам определить положение отрезков, которые будут использоваться для создания проекции на плоскости.
Проекции прямой на плоскость являются важным инструментом в геометрии и используются для решения различных задач. Понимание основных принципов и методов создания проекций на плоскости позволяет более точно и эффективно анализировать и решать геометрические задачи.
Зачем нужно строить проекцию прямой на плоскость?

Основная цель построения проекции состоит в том, чтобы получить более удобное и наглядное представление прямой на плоскости, что позволяет нам производить более точные вычисления и анализировать ее характеристики.
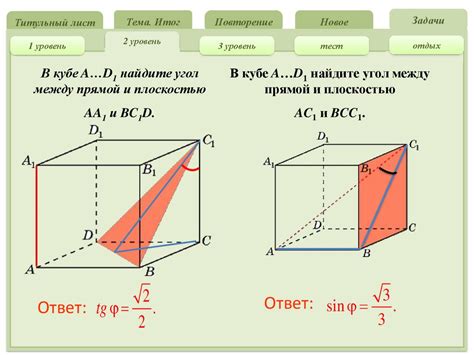
Проекция прямой может быть использована в различных областях, включая геометрию, инженерное дело, архитектуру, графический дизайн и другие. Она позволяет нам распознавать и оценивать положение, углы и длины отрезков прямой на плоскости.
Построение проекции прямой на плоскость также помогает нам визуализировать и понять взаимное расположение множества прямых и других объектов на плоскости. Это особенно полезно при работе с трехмерными объектами и построении трехмерных моделей.
Таким образом, строение проекции прямой на плоскость играет важную роль в нашем понимании геометрических объектов и помогает нам решать различные математические и инженерные задачи с учетом их особенностей в пространстве.
Как строить проекцию прямой на плоскость?

Для начала, нам необходимо знать уравнение прямой в пространстве. Обычно уравнение прямой записывается в виде y = kx + b, где k - это коэффициент наклона, а b - это коэффициент сдвига по оси Y.
Для построения проекции прямой на плоскость следуйте этим шагам:
- Задайте систему координат на плоскости. Оси X и Y будут основными осями, которые будут использоваться для отображения прямой.
- Постройте оси X и Y с соответствующими масштабами. Здесь важно выбрать подходящий масштаб для отображения всей прямой на плоскости.
- Используя уравнение прямой, постройте несколько точек на прямой, выбрав различные значения x. Например, можно выбрать 2-3 значения x и подставить их в уравнение, чтобы получить соответствующие значения y.
- Соедините полученные точки прямой с помощью линий. Это визуализирует проекцию прямой на плоскость.
Построение проекции прямой на плоскость может быть сложной задачей, особенно если прямая имеет большой угол наклона или проходит через оси координат. Но с практикой и пониманием основных принципов геометрии, вы сможете с легкостью строить проекции прямых на плоскости.
Какие существуют методы построения проекции прямой на плоскость?

Существует несколько методов, позволяющих построить проекцию прямой на плоскость. Каждый метод имеет свои особенности и применим в определенных ситуациях.
- Метод параллельных линий. Этот метод основан на том, что параллельные линии на плоскости имеют одинаковую проекцию. Для построения проекции прямой нужно провести из каждой точки прямой параллельные линии на плоскости и обозначить точки пересечения этих линий с плоскостью. Затем соединить эти точки линией и получится проекция прямой.
- Метод перпендикулярных линий. Этот метод заключается в том, чтобы провести из каждой точки прямой перпендикулярные линии на плоскость и найти точки пересечения этих линий с плоскостью. Затем соединить эти точки линией и получится проекция прямой. В отличие от метода параллельных линий, в этом методе не требуется наличие параллельных линий на плоскости.
- Метод плоскостей проекций. В этом методе используются специальные плоскости проекций – фронтальная, горизонтальная и профильная плоскости. Проекция прямой получается как пересечение плоскости проекций с плоскостью. Для построения проекции прямой нужно провести перпендикуляры из каждой точки прямой на плоскости проекций и найти точки пересечения этих перпендикуляров с плоскостью. Затем соединить эти точки линией и получится проекция прямой.
Каждый из этих методов имеет свои преимущества и недостатки, и выбор метода зависит от конкретной ситуации и требований постановки задачи. Важно уметь применять разные методы и выбирать наиболее подходящий в каждой конкретной ситуации.
Применение проекции прямой на плоскость в практических задачах
- Архитектура и строительство: при проектировании зданий и сооружений необходимо учитывать взаимное расположение различных элементов. Проекция прямой на плоскость позволяет определить планарность и прямолинейность различных элементов здания, таких как стены, потолки, лестницы и другие конструкции.
- Геодезия и картография: проекция прямой на плоскость используется для построения карт, измерения расстояний и высот на местности. Это позволяет определить точные координаты и границы территорий, проводить топографическую съемку и создавать географические карты.
- Машиностроение: при разработке и производстве деталей и механизмов необходимо учитывать их форму и геометрические размеры. Проекция прямой на плоскость помогает определить форму и размеры деталей, их точное расположение и взаимодействие в составе механизма.
- Дизайн и искусство: в визуальном и графическом искусстве проекция прямой на плоскость используется для создания перспективных рисунков и композиций. Это позволяет передать объем и глубину изображения, создать иллюзию пространства и движения.
Проекция прямой на плоскость является полезным инструментом во многих областях и находит применение в различных задачах. Понимание основных принципов проекции прямой позволяет более точно решать практические задачи и достигать желаемых результатов.
Руководство по строительству проекции прямой на плоскость для начинающих
Для начала, вам понадобятся основные инструменты: линейка, угольник и карандаш. Также приготовьте лист бумаги и нанесите на него систему координат - ось X и ось Y. Ось X будет служить основной направляющей для проекции прямой.
Шаг 1: Найдите точку начала (A) прямой и отметьте ее на листе. Затем откладывайте на оси X и оси Y значения координат прямой. Обозначьте эти точки на листе.
Шаг 2: Соедините точки, полученные на предыдущем шаге, линией. Это будет прямая, заданная в трехмерном пространстве.
Шаг 3: Проведите вертикальные линии из точек на прямой и пересеките их с осью X. Это будут точки проекции прямой на плоскость.
Шаг 4: Проведите линию, соединяющую точки проекции на оси X. Это и будет проекция прямой на плоскость.
Шаг 5: Если требуется, повторите шаги 1-4 для других прямых объектов.
Помните, что построение проекции прямой на плоскость требует внимательности и точности при измерениях. Практикуйтесь и постепенно сможете строить более сложные проекции и решать графические задачи.
Не забывайте сохранять свои работы, чтобы в дальнейшем использовать их в документации или презентациях. Удачи в освоении навыка построения проекций прямых на плоскость!