Построение проекции прямой на плоскость: подробный гайд и примеры

Проекция прямой на плоскость – это одна из важнейших задач в графическом моделировании и компьютерной графике. Она позволяет отобразить трехмерные объекты на двумерном экране, сохраняя при этом их пропорции и геометрические свойства.

Умение строить проекции прямых является неотъемлемой частью работы архитекторов, инженеров и дизайнеров. В данной статье мы рассмотрим подробный гайд по построению проекции прямой на плоскость, а также приведем несколько примеров, чтобы лучше понять эту технику.

Для начала нужно понять, что проекция – это отображение точек одной плоскости на другую. В случае проекции прямой на плоскость, мы берем всю прямую, находим ее пересечение со зрительной плоскостью и отображаем эту точку на плоскость проекций. Определение данной точки является ключевым моментом в построении проекции прямой на плоскость.

Что такое проекция прямой на плоскость и зачем она нужна?

Проекция прямой отображает на плоскости только часть прямой, т.е. ее проекцию. Проекция может быть параллельной или сходящейся, в зависимости от положения прямой и плоскости. Параллельная проекция сохраняет углы между прямой и плоскостью, а сходящаяся проекция изменяет углы.

Зачем нужна проекция прямой на плоскость? Она позволяет упростить сложные пространственные задачи, разбивая их на более простые двумерные проблемы. Также проекции применяются для создания плоских изображений трехмерных объектов, например, в компьютерной графике и архитектурном проектировании. Они помогают визуализировать объекты на плоскости и делать рассчеты, связанные с их размерами и формами.

Проекция прямой на плоскость – это важный инструмент, который позволяет упростить и визуализировать сложные пространственные задачи. При работе с проекциями необходимо учитывать особенности математических методов и правил, чтобы получить точные и корректные результаты.

Какие методы можно использовать для построения проекции прямой на плоскость?

Один из наиболее распространенных методов - это построение проекции прямой на плоскость с помощью развертки. Этот метод основан на свойстве прямой, в котором она отображается на плоскость при проекции в виде отрезка. Для того чтобы построить проекцию, нужно развернуть каждый отрезок прямой на плоскости в соответствии с определенными правилами. Затем можно соединить развертки и получить искомую проекцию прямой на плоскость.

Еще один метод - это использование метода проекций параллельных линий. Для этого нужно найти две точки на прямой, которые лежат в плоскости, на которую будет проецироваться прямая. Затем провести параллельные линии через эти точки на плоскость. Точки пересечения этих линий с плоскостью будут точками проекции. Для получения проекции прямой можно соединить эти точки.

Также существует метод построения проекции прямой на плоскость с использованием матриц. Этот метод основан на применении матриц преобразований, которые позволяют изменить координаты прямой в трехмерном пространстве и получить ее проекцию на плоскость. Для этого нужно умножить вектор координат прямой на матрицу преобразования. Результатом будет вектор координат проекции прямой на плоскость.

Метод развертки;
Метод проекций параллельных линий;
Метод матриц.

Каждый из этих методов имеет свои преимущества и недостатки и может быть применен в зависимости от конкретной задачи. Выбор метода зависит от вида прямой и плоскости, а также от требуемой точности и удобства выполнения расчетов.

Метод проекции прямой на плоскость с использованием векторов

Для начала необходимо определить векторы, которые задают прямую и плоскость. Представим прямую в виде направляющего вектора и точки, через которую прямая проходит. Также выберем два направляющих вектора для плоскости.

Используя скалярное произведение, найдем проекцию вектора направления прямой на плоскость. Для этого выполним скалярное произведение направляющего вектора прямой и одного из направляющих векторов плоскости. Полученное значение будет равно модулю векторной проекции.

Далее, для получения координат точки, в которой проецируется начало вектора направления прямой, нужно умножить найденную модуль проекции на нормализованный вектор направления прямой и проектировать его на плоскость.

Итак, метод проекции прямой на плоскость с использованием векторов следующий:

Определить векторы, задающие прямую и плоскость.
Вычислить скалярное произведение направляющего вектора прямой и одного из направляющих векторов плоскости.
Найти модуль векторной проекции.
Умножить модуль проекции на нормализованный вектор направления прямой.
Проектировать полученный вектор на плоскость и получить координаты точки, в которой произошла проекция.

Этот метод позволяет получить точечную проекцию прямой на плоскость, и может быть использован в различных областях, включая геометрию, графику и компьютерное моделирование.

Метод проекции прямой на плоскость с использованием уравнений прямых и плоскостей

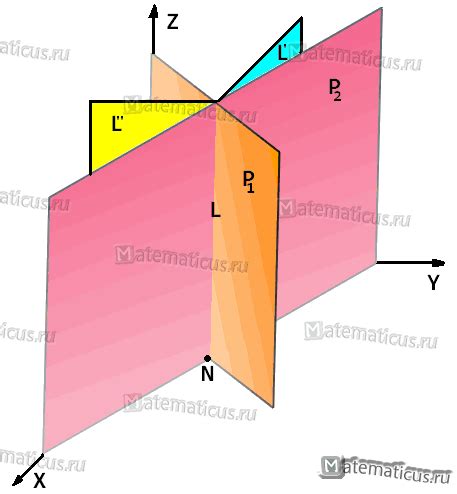
Для проекции прямой на плоскость с использованием уравнений прямых и плоскостей необходимо знать уравнения прямой и плоскости. Уравнение прямой определяет ее положение в пространстве, а уравнение плоскости - положение плоскости.

Чтобы найти проекцию прямой на плоскость, необходимо выполнить следующие шаги:

Найти точку пересечения прямой и плоскости. Для этого решите систему уравнений прямой и плоскости.
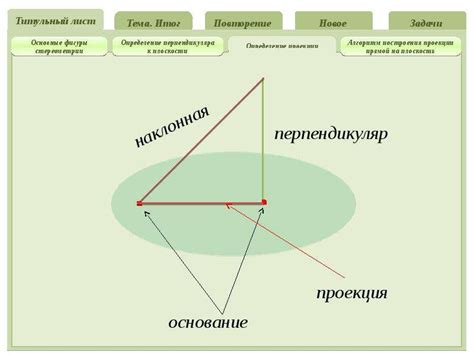
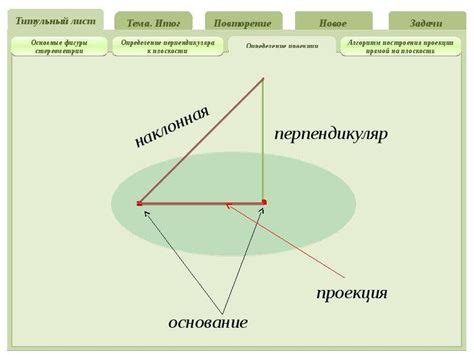
Проведите нормаль из точки пересечения на плоскость. Нормаль - это линия, перпендикулярная плоскости.
Определите точку на плоскости, через которую проходит нормаль. Эта точка будет служить началом проекции прямой.
Постройте проекцию прямой на плоскость с использованием начальной точки и направления прямой.

Метод проекции прямой на плоскость с использованием уравнений прямых и плоскостей позволяет точно определить положение и форму проекции. Он находит широкое применение в различных областях, таких как графика, геометрия и инженерия.

Используя уравнения прямых и плоскостей, вы можете проецировать прямые на плоскости с высокой точностью и получать информацию о их взаимном расположении и пересечении.

Примеры построения проекции прямой на плоскость

Ниже приведены несколько примеров, показывающих как можно построить проекцию прямой на плоскость:

Пример 1: Прямая задана уравнением $y = 2x + 1$ . Чтобы построить ее проекцию на плоскость, можно использовать следующий алгоритм:
1. Выбрать несколько значений для $x$ , например, -1, 0 и 1.
2. Подставить эти значения в уравнение прямой и вычислить соответствующие значения для $y$ .
3. Полученные точки ( $x$ , $y$ ) являются проекциями точек прямой на плоскость.
4. Нарисовать проекции точек и соединить их прямой.
Пример 2: Прямая задана двумя точками A(2, 3) и B(5, 1). Чтобы построить ее проекцию на плоскость, можно использовать следующий алгоритм:
1. Найти вектор направления прямой, вычислив разность координат точек: $AB = B - A = (5 - 2, 1 - 3) = (3, -2)$ .
2. Найти вектор нормали к плоскости, на которую проектируется прямая. В данном случае, подойдет например вектор $n = (1, 0)$ .
3. Вычислить скалярное произведение вектора направления на вектор нормали: $d = AB · n = (3, -2) · (1, 0) = 3$ .
4. Найти проекцию вектора направления на вектор нормали, умножив вектор нормали на скалярное произведение: $p = d * n = 3 * (1, 0) = (3, 0)$ .
5. Полученный вектор $p$ является вектором проекции.
6. Построить прямую, проходящую через точку A и параллельную вектору проекции $p$ .
Пример 3: Прямая задана параметрическим уравнением $x = t, y = 2t + 1$ . Чтобы построить ее проекцию на плоскость, можно использовать следующий алгоритм:
1. Выбрать несколько значений для параметра $t$ , например, 0, 1 и 2.
2. Подставить эти значения в параметрические уравнения и вычислить соответствующие значения для $x$ и $y$ .
3. Полученные точки ( $x$ , $y$ ) являются проекциями точек прямой на плоскость.
4. Нарисовать проекции точек и соединить их прямой.

Это лишь несколько примеров способов построения проекции прямой на плоскость. В зависимости от задачи и доступных данных, можно использовать различные методы и подходы. Важно помнить, что построение проекции является одним из основных инструментов геометрии и находит применение в различных областях науки и техники.

Применение проекции прямой на плоскость в реальной жизни

1. Архитектура и строительство:

При создании планов зданий и помещений инженеры и архитекторы используют проекции прямой на плоскость для определения расположения стен, окон, дверей и других элементов.
Подобным образом проекции применяются при проектировании и создании ландшафтных планов, где необходимо отобразить контуры и форму ландшафтного дизайна.

2. Графика и дизайн:

В компьютерной графике проекции прямой на плоскость используются для создания перспективных изображений и визуализации трехмерных объектов.
Дизайнеры могут применять проекции прямой на плоскость, чтобы создавать реалистичные и пропорциональные изображения объектов и архитектурных структур.

3. Инженерия и автомобильная промышленность:

В автомобильной промышленности проекции прямой на плоскость используются для создания чертежей и планов автомобилей, позволяющих инженерам определить форму кузова, размеры и расположение компонентов.
Проективные методы также применяются в инженерных расчетах и проектах, где необходимо определить точные геометрические параметры объектов и их взаимосвязь.

4. География:

Проекции применяются в географии для отображения поверхности Земли на плоскость, что позволяет создавать карты и навигационные системы.
Различные типы проекций прямой на плоскость используются для различных целей, например, равноугольные проекции используются для изображения океанов и континентов, а равноплощадные проекции используются для показа правильных пропорций площадей и расстояний.

Все вышеупомянутые области применения проекции прямой на плоскость подчеркивают важность этого инструмента при работе с пространственными данными и геометрическими объектами. Знание и понимание проекции прямой на плоскость позволяет лучше визуализировать и анализировать объекты в трехмерном пространстве.

Построение проекции прямой на плоскость — подробный гайд и примеры