Прямая регрессия - один из основных инструментов статистического анализа, который позволяет оценить взаимосвязь между двумя переменными. Данная статья предлагает шаг за шагом разобраться в построении прямой регрессии, а также дает полезные советы для тех, кто только начинает изучать эту тему.

Основная идея прямой регрессии заключается в том, что мы строим прямую линию, которая наилучшим образом описывает зависимость между переменными. Для этого нужно иметь набор данных, содержащий значения обоих переменных - независимой (x) и зависимой (y). С помощью метода наименьших квадратов определяются коэффициенты прямой, которые минимизируют ошибку предсказания.

Первый шаг в построении прямой регрессии - визуализация данных. График рассеяния (scatter plot) поможет нам увидеть, насколько сильно зависимая переменная меняется в зависимости от изменений независимой переменной. Если наблюдается явная линейная зависимость, значит, мы можем применить прямую регрессию. Если же зависимость нелинейная, то для анализа необходимо использовать другие методы.

Далее необходимо рассчитать коэффициенты прямой регрессии. Для этого используются специальные алгоритмы и формулы, которые позволяют найти наилучшие значения коэффициентов. Полученные коэффициенты t-статистически значимы, если их значения превышают критическое значение их t-статистики. Результаты регрессионного анализа стоит интерпретировать с осторожностью и проверить на соответствие условиям применимости модели.

Конечно, чтобы полностью овладеть методом прямой регрессии, требуется глубокое понимание статистических методов и математических алгоритмов. Однако, этот материал поможет вам начать изучение данной темы и научиться строить простые модели. Будьте готовы к экспериментированию и продолжайте совершенствовать свои навыки анализа данных!

Что такое прямая регрессия?

В прямой регрессии исследуется связь между зависимой переменной (y) и независимой переменной (x). Зависимая переменная может быть количественной или непрерывной, в то время как независимая переменная обычно является фактором или причиной, влияющей на зависимую переменную.

Цель прямой регрессии - найти линию (или гиперплоскость в случае более высоких размерностей), которая наилучшим образом описывает связь между переменными. Эта линия предсказывает значения зависимой переменной на основе значений независимой переменной.

Прямая регрессия часто используется для прогнозирования будущих значений зависимой переменной на основе известных значений независимой переменной. Модель прямой регрессии может быть использована для анализа данных, выявления тенденций и предсказания результатов событий.

Прямая регрессия может быть линейной или нелинейной, в зависимости от формы отношения между переменными. Линейная прямая регрессия описывается уравнением y = a + bx, где a - точка пересечения с осью y (свободный член), b - коэффициент наклона прямой, x - значение независимой переменной.

Прямая регрессия - мощный инструмент анализа данных, который может помочь в понимании отношений между переменными и прогнозировании будущих значений. Он широко применяется в различных областях, включая экономику, финансы, маркетинг, медицину, социальные науки и инженерию.

Цели построения прямой регрессии

Прямая регрессия позволяет предсказать значения зависимой переменной на основе измеренных значений независимых переменных. Это может быть полезно для прогнозирования будущих событий или оценки влияния различных факторов на исследуемый процесс. Кроме того, прямая регрессия может использоваться для проверки гипотез о наличии статистически значимой связи между переменными или для оценки силы этой связи.

Результаты построения прямой регрессии могут быть представлены в виде уравнения прямой, которое описывает зависимость переменной y от переменной x. Это позволяет упростить анализ данных и прогнозирование будущих значений. Также результаты прямой регрессии могут быть визуализированы на графике, что упрощает их интерпретацию и позволяет выявить тенденции и аномалии в данных.

Построение прямой регрессии требует выбора адекватной модели, а также оценки параметров этой модели на основе доступных данных. Для достижения этой цели необходимо иметь набор данных, содержащий измерения зависимой и независимых переменных. Кроме того, необходимо учитывать предпосылки и ограничения модели прямой регрессии, а также проверять ее адекватность и точность с помощью соответствующих статистических методов.

В целом, построение прямой регрессии является важным инструментом для анализа данных и исследования связей между переменными. Он может быть использован для прогнозирования, моделирования и проверки гипотез, а также для понимания влияния различных факторов на исследуемый процесс. Освоение этого метода поможет исследователям и аналитикам получить ценные и полезные результаты при анализе данных и принятии решений на основе этих данных.

Выбор модели для прямой регрессии

Вот несколько советов, которые помогут вам выбрать подходящую модель:

1. Знание предметной области

Чтобы выбрать правильную модель, необходимо иметь хорошее представление о предметной области и ожидаемых взаимосвязях между переменными. Исследуйте данные, изучите предшествующие исследования и примените свои знания, чтобы определить, какая модель может лучше всего описывать зависимость.

2. Проверка предположений модели

Прямая регрессия основана на нескольких предположениях, включая линейность, независимость ошибок и нормальное распределение ошибок. Проверьте эти предположения, используя диагностические графики и статистические тесты. Если предположения нарушаются, необходимо рассмотреть альтернативные модели.

3. Выбор переменных

Выбор правильных переменных для модели является одним из самых сложных и важных аспектов прямой регрессии. Используйте здравый смысл, статистические методы и оценки значимости переменных, чтобы определить, какие переменные должны быть включены в модель. Избегайте мультиколлинеарности и учитывайте возможность нелинейных взаимосвязей.

4. Оценка качества модели

Важно оценить качество модели, чтобы узнать, насколько хорошо она описывает данные и делает прогнозы. Используйте статистические метрики, такие как коэффициент детерминации (R-квадрат), корреляция, а также графические методы, например, разбросные диаграммы и графики остатков.

Правильный выбор модели для прямой регрессии позволит вам получить более точные прогнозы и лучше понять взаимосвязи между переменными. Помните, что выбор модели - это искусство, требующее опыта и разумного подхода.

Сбор и подготовка данных для прямой регрессии

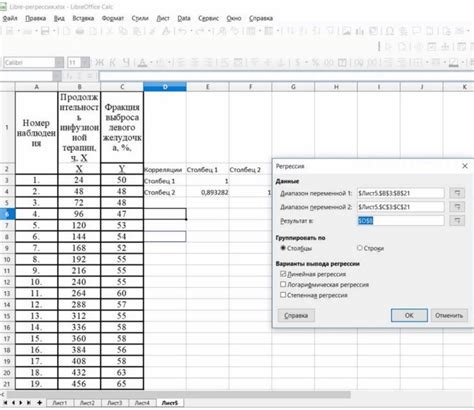
Сбор данных:

Первый шаг состоит в сборе нужных данных для анализа. Данные могут быть получены различными способами – наблюдениями, измерениями, опросами и т.д. Основное требование – данные должны быть релевантными и достоверными для поставленной задачи. Важно также учитывать, что объем данных должен быть достаточным для обеспечения надежности модели.

Предобработка данных:

После сбора данных, следующий шаг – их предобработка. Здесь необходимо провести несколько действий, для того чтобы данные стали пригодными для дальнейшего анализа:

1. Удаление выбросов: аномальные значения, которые сильно отличаются от остальных элементов выборки, могут исказить результаты модели. Поэтому такие выбросы стоит удалить или корректировать.
2. Заполнение пропущенных значений: если в данных встречаются пропущенные значения, то необходимо решить, каким образом эти значения будут заполнены. Можно использовать различные методы, например, заполнение средним или медианным значением.
3. Нормализация данных: чтобы данные были однородными и могли быть сравниваемыми, их следует нормализовать. Например, можно провести стандартизацию значений путем вычитания среднего и деления на стандартное отклонение.
4. Кодирование категориальных переменных: если в данных присутствуют категориальные переменные, их необходимо преобразовать в числовые значения. Для этого можно использовать методы кодирования, такие как one-hot encoding или label encoding.

После проведения этих шагов, можно считать, что данные готовы для прямой регрессии. Важно помнить, что подготовка данных – постоянный и итерационный процесс. Возможно, потребуется провести несколько циклов сбора и предобработки информации для достижения наилучших результатов.

Выбор алгоритма построения прямой регрессии

Один из наиболее распространенных алгоритмов - метод наименьших квадратов. Он заключается в минимизации суммы квадратов расстояний между фактическими значениями y и предсказанными значениями, полученными с помощью линейной модели. Этот метод довольно прост в реализации и обладает хорошей точностью при небольших объемах данных.

Еще одним алгоритмом, который может быть полезным при построении прямой регрессии, является метод градиентного спуска. Он отличается тем, что позволяет оптимизировать параметры модели, путем итеративного обновления их значений с использованием градиента функции потерь. Этот метод может быть полезен в случаях, когда объем данных большой и требуется оптимизация модели.

Также существуют другие алгоритмы, например, методы регуляризации, которые позволяют учесть особенности данных и предотвратить переобучение модели. Один из таких методов - гребневая регрессия, которая добавляет штраф к большим значениям параметров модели.

При выборе алгоритма построения прямой регрессии необходимо учитывать особенности данных, объем выборки и требования к точности модели. Кроме того, полезно проводить сравнительный анализ различных алгоритмов и проводить тестирование модели на независимой выборке данных, чтобы оценить ее качество и устойчивость.

Оценка качества прямой регрессии

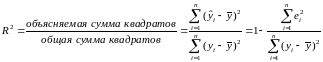
Существует несколько показателей, которые помогают оценить качество прямой регрессии:

1. Коэффициент детерминации (R²)

Коэффициент детерминации показывает, какую долю вариации зависимой переменной можно объяснить с помощью независимой переменной. Он принимает значения от 0 до 1, где 0 означает, что прямая регрессии не объясняет вариацию, а 1 означает, что прямая регрессии полностью объясняет вариацию.

2. Стандартная ошибка регрессии (SE)

Стандартная ошибка регрессии показывает, как далеко в среднем истинные значения зависимой переменной могут отклоняться от прямой регрессии. Чем меньше значение стандартной ошибки регрессии, тем лучше прямая регрессии аппроксимирует данные.

3. Коэффициенты регрессии (a и b)

Коэффициенты регрессии a и b показывают, каким образом независимая переменная влияет на зависимую переменную. Коэффициент a показывает сдвиг прямой регрессии по оси y, а коэффициент b показывает наклон прямой.

При оценке качества прямой регрессии важно учитывать контекст и особенности конкретной задачи, так как разные показатели могут быть значимыми для разных ситуаций.

Советы для начинающих по построению прямой регрессии

Построение прямой регрессии может быть сложным заданием для начинающих, но с правильным подходом и советами вы сможете справиться успешно. Здесь мы предлагаем несколько полезных советов, которые могут помочь вам в этом процессе.

1. Изучите основы статистики: Понимание основных понятий и методов статистики, таких как коэффициент корреляции и практика использования их в решении задач регрессии, поможет вам получить более глубокое понимание этой темы.
2. Соберите достаточное количество данных: Чем больше данных у вас есть, тем более точной будет ваша модель регрессии. При сборе данных обратите внимание на релевантность исследуемых переменных и их взаимосвязь с зависимой переменной.
3. Постройте график рассеяния: Визуализация данных в виде графика рассеяния поможет вам оценить наличие или отсутствие линейной зависимости между переменными. Также это поможет вам определить возможные выбросы, которые могут искажать результаты регрессии.
4. Выполните предварительный анализ: Проанализируйте данные на наличие пропущенных значений, выбросов и других аномалий. Определите, требуется ли устранение этих аномалий или они могут быть объяснены особенностями набора данных.
5. Выберите адекватную модель: Существует несколько моделей регрессии, включая простую линейную регрессию, множественную регрессию и полиномиальную регрессию. Выберите модель, которая наиболее адекватно описывает взаимосвязь между переменными в вашем конкретном случае.
6. Оцените качество модели: Используйте различные статистические метрики, такие как коэффициент детерминации (R-квадрат), среднеквадратичная ошибка (MSE) и средняя абсолютная ошибка (MAE), чтобы оценить качество вашей модели. Это поможет вам понять, насколько хорошо ваша модель соответствует данным.
7. Интерпретируйте результаты: После построения модели и получения результатов, необходимо проанализировать и интерпретировать их. Оцените важность и вклад каждой независимой переменной в предсказание зависимой переменной.
8. Учитесть ограничений: Помните, что регрессия имеет свои ограничения. Например, она предполагает линейность зависимости между переменными и отсутствие мультиколлинеарности. Будьте осторожны при интерпретации результатов и представлении их в контексте вашей исследовательской задачи.

Следуя этим советам, вы сможете лучше понять и применять методы прямой регрессии для анализа данных и предсказания зависимой переменной на основе независимых переменных.