Регрессионный анализ является одним из наиболее распространенных методов в статистике, позволяющим предсказывать значения одной переменной на основе других переменных. Он находит широкое применение в различных областях, включая экономику, финансы, маркетинг и многое другое.

R - мощное программное обеспечение для статистического анализа и визуализации данных. В данном руководстве мы рассмотрим, как использовать R для построения регрессионной модели. Мы покажем, как подготовить данные, выбрать подходящую модель, оценить ее качество и использовать полученные результаты для прогнозирования.

Для начала работы с регрессионной моделью в R, нам понадобится установить и подключить несколько пакетов, таких как "dplyr", "tidyverse" и "broom" – они помогут нам обработать и визуализировать данные, а также оценить качество модели. Затем мы сможем загрузить наши данные и начать работу над построением модели.

В данном руководстве мы представим шаги построения регрессионной модели в R на примере реальных данных. Мы приведем подробную информацию о каждом шаге и комментарии к коду, чтобы вы могли легко повторить все действия самостоятельно. Готовы начать? Давайте приступим к построению регрессионной модели в R!

Выбор и подготовка данных для модели

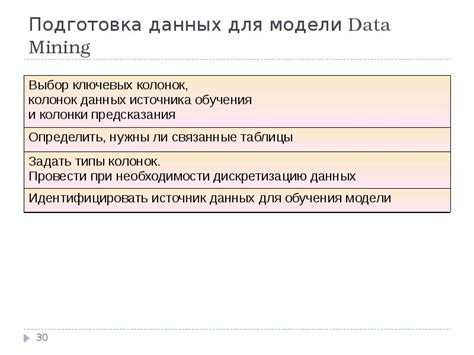
Прежде чем приступить к выбору данных, необходимо понять, какие переменные могут оказывать влияние на зависимую переменную, которую мы хотим предсказать. Это может быть статистический анализ, предварительные исследования или экспертные знания. Важно выбрать переменные, которые имеют смысл и могут быть логически объяснены.

После выбора переменных необходимо проверить данные на наличие пропущенных значений и аномалий. Пропущенные значения могут искажать результаты модели, поэтому их необходимо обработать. Для этого можно использовать различные методы, такие как удаление пропущенных значений, заполнение средним или медианным значением, использование алгоритмов заполнения пропусков и т.д.

Также необходимо проверить данные на наличие выбросов и аномалий. Выбросы могут искажать распределение данных и влиять на точность модели. При обнаружении выбросов можно удалить соответствующие наблюдения или применить методы обработки выбросов, такие как замена выбросов медианами или применение алгоритмов обнаружения аномалий.

Кроме того, данные могут также быть нормализованы или стандартизированы для обеспечения сравнимости и согласованности значения переменных. Нормализация выполняется путем приведения данных к определенному диапазону, например, от 0 до 1. Стандартизация предполагает приведение данных к форме с нулевым средним и единичной дисперсией.

Выбор и подготовка данных являются важными этапами построения регрессионной модели. Они определяют качество результатов моделирования и достоверность предсказаний. Тщательный анализ данных и проведение соответствующих манипуляций с данными позволят получить более точную и надежную модель.

Определение зависимой переменной

Выбор правильной зависимой переменной является одним из самых важных этапов в построении регрессионной модели. Она должна быть хорошо измерена и иметь сильную связь с интересующими нас факторами.

Зависимая переменная должна отвечать следующим требованиям:

• Измеряемость: зависимая переменная должна быть количественной, то есть иметь числовые значения.
• Вариативность: зависимая переменная должна изменяться и иметь достаточную вариативность в значениях для анализа.
• Постоянство: зависимая переменная должна относительно постоянно меняться в данных, чтобы можно было исследовать ее связь с другими переменными.
• Зависимость: зависимая переменная должна быть зависимой от других переменных, чтобы можно было построить модель, предсказывающую и объясняющую ее значения на основе независимых переменных.

Определение правильной зависимой переменной требует внимательного анализа и предварительных исследований. Она может быть как числовой, так и категориальной, в зависимости от поставленной задачи и природы данных.

Выбор правильной зависимой переменной является важным шагом в построении регрессионной модели и может сильно влиять на результаты и качество моделирования. Тщательно проанализируйте данные и сделайте обоснованный выбор зависимой переменной для достижения поставленных целей.

Выбор независимых переменных

При выборе независимых переменных необходимо учитывать следующие вопросы:

1. Релевантность: Независимая переменная должна иметь значимое влияние на зависимую переменную. Переменная должна быть понятной с точки зрения логики и иметь теоретическую обоснованность.
2. Мультиколлинеарность: Независимые переменные не должны быть сильно коррелированы между собой. В случае сильной корреляции, одну из переменных следует удалить из модели или объединить их в одну переменную.
3. Статистическая значимость: Независимая переменная должна быть статистически значима и иметь значительный вклад в объяснение вариации зависимой переменной. Это можно оценить с помощью значений коэффициентов регрессии и уровня значимости p-value.
4. Научная значимость: Независимая переменная должна иметь научную или практическую значимость для исследования или задачи, которую вы пытаетесь решить.
5. Доступность данных: Независимые переменные должны быть доступными для исследования. Если данные отсутствуют или сложно получить, то эти переменные нельзя использовать в модели.

Выборка независимых переменных может быть сложным процессом, требующим глубокого понимания предметной области, а также использование различных методов, таких как анализ корреляции, t-тесты и пр.

Помимо выбора независимых переменных, также важно учитывать их взаимодействие и нелинейные эффекты при построении модели. Все эти аспекты помогут сформировать правильную и точную регрессионную модель.

Построение модели и подгонка данных

Первым шагом в построении модели является подготовка данных. Это включает в себя загрузку данных в R, просмотр их структуры и очистку от пропущенных значений.

После подготовки данных можно приступать к построению модели. В R для этого используется функция lm(), которая позволяет построить линейную регрессионную модель. Например, чтобы построить модель, где зависимая переменная y связана с независимыми переменными x1 и x2, можно использовать следующий код:

model

В этом коде lm() - функция для построения линейной регрессионной модели, y ~ x1 + x2 - формула, описывающая зависимость переменной y от переменных x1 и x2, dataset - название вашего датасета, в котором содержатся все переменные.

summary(model)

В результате будет выведена информация о значениях коэффициентов модели, их статистической значимости, а также другие показатели, помогающие оценить качество модели.

Когда модель построена и результаты проанализированы, можно использовать ее для прогнозирования новых значений зависимой переменной на основе заданных значений независимых переменных. Для этого используется функция predict(). Например, чтобы получить прогнозное значение для переменной y при заданных значениях x1 и x2, можно использовать следующий код:

new_data

Таким образом, построение модели и подгонка данных в R - это мощный инструмент для анализа и прогнозирования зависимых переменных на основе независимых переменных. R предлагает множество функций и пакетов, которые облегчают работу с регрессионными моделями и позволяют получить обширные результаты анализа.

Оценка значимости коэффициентов модели

После построения регрессионной модели важно оценить значимость коэффициентов, чтобы понять, какие переменные наиболее сильно влияют на зависимую переменную.

В R для оценки значимости коэффициентов применяются различные методы и тесты. Один из наиболее распространенных способов - t-тест.

Для проведения t-теста в R необходимо вызвать функцию coef() для объекта модели и передать ей аргумент test = "t".

Результатом t-теста является таблица, в которой указывается каждый коэффициент модели, его оценка, стандартная ошибка, значение t-статистики и p-значение - вероятность получения наблюдаемого значения t-статистики или более экстремальное, при условии, что нулевая гипотеза верна (коэффициент равен нулю).

Важно отметить, что малое p-значение указывает на значимость коэффициента, то есть отвергание нулевой гипотезы.

Еще одним способом оценки значимости коэффициентов является построение доверительных интервалов. Доверительный интервал указывает на то, с какой вероятностью находится истинное значение коэффициента в заданном интервале.

В R для построения доверительных интервалов можно использовать функцию confint(), которая возвращает интервалы для каждого коэффициента.

Вы можете выбрать наиболее подходящий метод оценки значимости коэффициентов в зависимости от своих задач и предпочтений.

Анализ ошибок и улучшение модели

После построения регрессионной модели важно проанализировать ошибки предсказаний и найти способы улучшения модели. В данном разделе мы рассмотрим несколько методов анализа ошибок и предложим возможные пути для улучшения модели.

1. Анализ остатков

   Для начала рекомендуется проанализировать остатки модели - разницу между фактическими значениями и предсказанными значениями модели. Остатки должны иметь нулевое среднее и быть случайно распределенными без видимой структуры. Если остатки имеют какие-либо систематические закономерности, это может указывать на наличие некоторых проблем в модели, которые следует устранить.

2. Изучение важности переменных

   Вторым шагом может быть изучение важности переменных в модели. Существует несколько подходов для определения важности переменных, включая коэффициенты регрессии, относительное влияние переменных на предсказания модели и значимость коэффициентов.

3. Добавление новых переменных

   Если анализ остатков и важности переменных указывают на дефекты или недостатки модели, можно попробовать добавить новые переменные, которые могут лучше объяснить зависимую переменную. Неплохо иметь теоретическую основу для добавления новых переменных, чтобы не "слепо" вносить изменения в модель.

4. Трансформация переменных

   Иногда трансформация переменных может помочь улучшить модель. Например, логарифмическое преобразование переменной может сделать ее зависимость с более линейной. Это может быть полезно, если модель не улавливает нелинейные зависимости.

5. Использование других моделей

   Если все вышеперечисленные способы не приводят к достаточному улучшению модели, можно попробовать использовать другие, более сложные модели. Например, можно попробовать использовать гребневую регрессию или случайный лес, в зависимости от особенностей данных и целей моделирования.

Анализ ошибок и улучшение модели это итеративный процесс, так как каждое изменение может повлиять на другие аспекты модели. Важно быть внимательным и методичным при анализе и улучшении модели, чтобы добиться наилучших результатов.