Сечения в тетраэдре являются важным элементом его изучения. Они позволяют нам лучше понять геометрические свойства этой фигуры и раскрыть её особенности. Построение сечений в тетраэдре требует некоторых знаний и навыков, но с нашей подробной инструкцией это задание станет гораздо проще.
Шаг 1: Прежде чем приступить к построению сечений в тетраэдре, необходимо вспомнить его геометрические характеристики. Тетраэдр – это правильная многогранная фигура, состоящая из четырех равносторонних треугольников. Она имеет четыре вершины и шесть ребер.
Шаг 2: Для построения сечений отметьте на ребрах тетраэдра точки, через которые будет проходить плоскость сечения. Затем соедините отмеченные точки прямыми линиями – это будет плоскость сечения в тетраэдре.
Шаг 3: Проверьте правильность построенной плоскости сечения. Убедитесь, что она проходит через все выбранные точки на ребрах тетраэдра.
Следуя этой подробной инструкции, вы сможете без труда построить сечения в тетраэдре. Это позволит вам лучше изучить геометрию и свойства этой уникальной фигуры.
Раздел 2: Определение сечения в тетраэдре
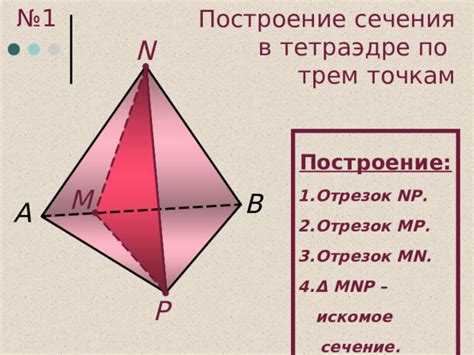
1. Метод пересечения плоскостью
- Выберите плоскость, которая будет служить сечением.
- Проведите эту плоскость через тетраэдр, пересекая все его грани.
- Запишите уравнение плоскости и найдите точки пересечения плоскости с каждой из граней тетраэдра.
- Полученные точки являются вершинами сечения.
2. Метод геометрической конструкции
- Выберите грань тетраэдра, через которую будет проходить сечение.
- На этой грани отметьте несколько точек.
- Проведите прямые линии через эти точки, пересекающие другие грани тетраэдра.
- Точки пересечения этих прямых линий с другими гранями являются вершинами сечения.
3. Метод численного моделирования
- Используйте компьютерное программное обеспечение для построения тетраэдра и определения его сечения.
- Вводите параметры тетраэдра и выбирайте метод определения сечения.
- Программа автоматически построит сечение и выведет его параметры.
Каждый из этих методов имеет свои особенности и подходит для разных ситуаций. Используйте тот метод, который наиболее удобен и прост для вашей задачи.
Раздел 3: Инструменты и материалы для построения сечений в тетраэдре
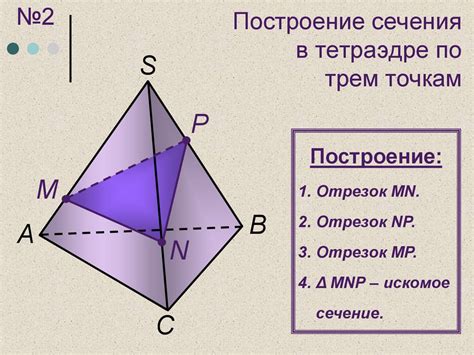
Построение сечений в тетраэдре требует использования определенных инструментов и материалов. В этом разделе представлен список необходимых элементов, которые помогут вам успешно выполнить эту задачу.
1. Линейка: для измерения длин сторон и отрезков на плоскости.
2. Карандаш: для обозначения точек и проведения линий на плоскости.
3. Геодезический треугольник: для построения прямых и приведения углов на плоскости.
4. Чистый лист бумаги: для нанесения построений и сечений.
5. Циркуль: для построения окружностей и дуг на плоскости.
6. Графический калькулятор: для выполнения вычислений и анализа геометрических фигур.
7. Компас: для построения окружностей и дуг на плоскости.
8. Ламинатор и пластиковые футляры: для сохранения и защиты построений и сечений.
Убедитесь, что вам доступны все перечисленные инструменты и материалы перед тем, как приступить к построению сечений в тетраэдре. Это позволит вам удобно и точно выполнять необходимые действия и получать качественные результаты.
Раздел 4: Шаг 1: Отметка начальной точки сечения в тетраэдре
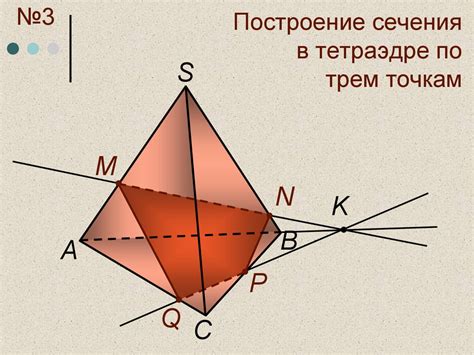
Для построения сечений в тетраэдре необходимо определить начальную точку сечения, которая будет использоваться в дальнейшем. Это поможет нам контролировать процесс построения и обеспечить точность результатов.
Для отметки начальной точки сечения в тетраэдре следуйте инструкциям:
- Рассмотрите тетраэдр со всеми его вершинами: A, B, C и D.
- Выберите любую из вершин тетраэдра и обозначьте ее как начальную точку сечения.
- Для удобства, рекомендуется выбирать вершину, ближе всего к месту, где вы желаете построить сечение.
После отметки начальной точки сечения, вы готовы перейти к следующему шагу: "Шаг 2: Выбор направления сечения".
Раздел 5: Шаг 2: Определение плоскости сечения в тетраэдре
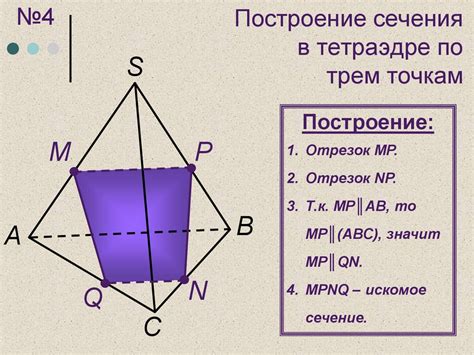
После того, как была произведена точка пересечения в предыдущем шаге, необходимо определить плоскость сечения в тетраэдре. Для этого используется три точки: начальная точка сечения, точка пересечения и какая-либо другая точка внутри тетраэдра.
Выбирается точка, находящаяся внутри тетраэдра и не совпадающая с начальной точкой сечения или точкой пересечения. Это может быть центр тяжести тетраэдра или любая другая подходящая точка.
Далее, используя найденные точки, строится плоскость сечения. Для этого можно использовать формулу плоскости, заданную векторами, проходящими через точки.
В результате будет получена плоскость, проходящая через все три точки и пересекающая тетраэдр.
После определения плоскости сечения можно приступить к построению самого сечения в тетраэдре.
Раздел 6: Шаг 3: Построение линии сечения в тетраэдре
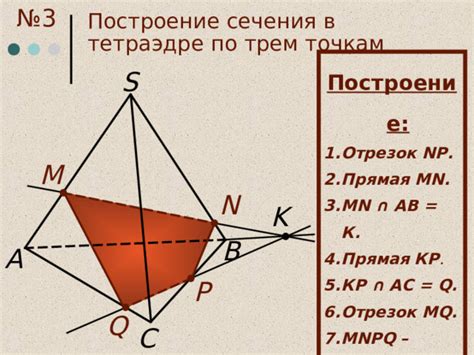
1. Возьмите свой тетраэдр и определите две точки, между которыми вы хотели бы построить линию сечения.
2. Возьмите карандаш и с помощью линейки нарисуйте прямую линию между этими двумя точками. Убедитесь, что линия проходит через все грани тетраэдра.
3. Внимательно посмотрите на тетраэдр, чтобы увидеть, где проходит линия сечения. Если это необходимо, обведите ее более толстой линией, чтобы она была хорошо видна.
4. Используя ножницы, аккуратно вырежьте тетраэдр по линии сечения. Будьте осторожны, чтобы не повредить другие части фигуры.
5. После вырезания линии сечения вы будете иметь две половинки тетраэдра, разделенные этой линией. Это станет вашими двумя секциями.
6. Для сохранения структуры тетраэдра после разделения, вы можете использовать клей или скотч, чтобы закрепить части фигуры вместе.
7. Теперь у вас есть две секции тетраэдра, которые можно использовать для изучения и анализа его внутренней структуры.
Примечание: Запаситесь несколькими тетраэдрами, чтобы практиковаться в построении различных линий сечения и изучении их эффектов на фигуру.
Раздел 7: Шаг 4: Построение фигуры сечения в тетраэдре
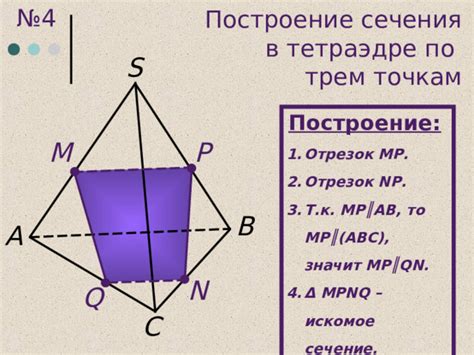
Продолжаем работу со сборкой нашего тетраэдра! В этом шаге мы будем строить фигуру сечения внутри тетраэдра.
1. Возьмите линейку и прокладывайте линию от одной из вершин тетраэдра до противоположной стороны. Это поможет нам определить точку сечения.
2. С помощью линейки нарисуйте отрезок от середины этой линии до вершины, на которую приходится сечение. Таким образом, вы построите медиану сечения.
3. Повторите шаги 1 и 2 для каждой стороны тетраэдра. Тем самым вы определите все точки сечения медиан с каждой стороной.
4. Затем соедините точки сечения медиан линиями. Получившийся многоугольник и будет фигурой сечения внутри тетраэдра.
5. Чтобы убедиться, что фигура сечения правильно построена, проверьте, что она проходит через все вершины тетраэдра.
6. При необходимости, отметьте фигуру сечения на тетраэдре карандашом или маркером, чтобы ее можно было визуально выделить.
Поздравляю! Теперь вы успешно построили фигуру сечения внутри тетраэдра.
Раздел 8: Примеры сечений в тетраэдре
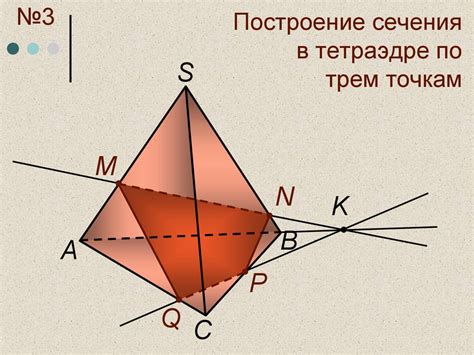
Пример 1: Горизонтальное сечение. Рассмотрим горизонтальную плоскость, которая проходит через середину ребра AB и перпендикулярная плоскости основания ABC. Это сечение разделит тетраэдр на две пирамиды и будет проходить через точку M, которая является серединой ребра AB и точкой пересечения плоскостей основания ABC.
Пример 2: Вертикальное сечение. Рассмотрим вертикальную плоскость, которая проходит через вершину D и перпендикулярная плоскости основания ABC. Это сечение разделит тетраэдр на два треугольных призмы и будет проходить через точку N, которая является вершиной D и точкой пересечения плоскостей основания ABC.
Пример 3: Случайное сечение. Рассмотрим плоскость, которая проходит через две вершины тетраэдра и не перпендикулярна плоскости основания ABC. Это сечение разделит тетраэдр на два наклонных параллелограмма и будет проходить через точку P, которая является точкой пересечения плоскостей сечения и плоскости основания ABC.
Раздел 9: Расширенные методы построения сечений в тетраэдре
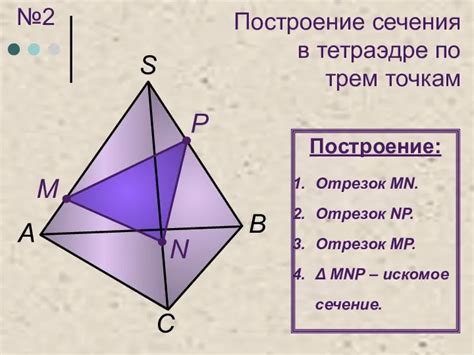
В предыдущих разделах мы рассмотрели основные методы построения сечений в тетраэдре. Теперь рассмотрим несколько более сложных и расширенных методов.
1. Метод разделения тетраэдра на подтетраэдры.
Для построения сечений с большей точностью, может потребоваться разделить исходный тетраэдр на несколько подтетраэдров. При этом, каждый подтетраэдр будет иметь меньший объем, что позволит получить более детализированное изображение сечений.
2. Использование дополнительных граней.
Кроме основных граней тетраэдра, можно добавить дополнительные грани, которые будут помогать визуализировать сечения. Так, например, можно добавить грани, которые будут показывать исходные плоскости сечений.
3. Использование гладких кривых.
Вместо прямолинейных границ на гранях тетраэдра, можно использовать гладкие кривые, такие как сплайны Безье или кривые Безье-сегменты. Это поможет сделать сечения более плавными и эстетически приятными.
4. Использование цветовой графики.
Для более наглядного отображения сечений, можно использовать цветовую графику. Например, можно задать разные цвета для разных частей сечения или использовать градиенты для плавного перехода цвета.
5. Использование алгоритмов визуализации сечений.
Существуют различные алгоритмы визуализации сечений, которые позволяют создавать трехмерные модели с более высокой детализацией. Некоторые из них используют метод трассировки лучей или приближенные методы, такие как метод конечных элементов.
Это лишь некоторые из методов, которые можно применять для построения сечений в тетраэдре с более высокой точностью и детализацией. Важно выбрать подходящий метод в зависимости от поставленных перед задачей требований.