Логическое выражение - это способ выразить отношения между различными элементами или условиями в языке логики. Оно состоит из утверждений, связанных логическими операторами, такими как И, ИЛИ и НЕ, и представляет собой последовательность символов, символизирующих различные логические связи. Построение схемы логического выражения - это визуальная интерпретация логического выражения, которая помогает наглядно представить связи между разными элементами.
Построение схемы логического выражения является важным инструментом для анализа и понимания сложных логических выражений. Оно позволяет наглядно представить, как работает логическое выражение и какие значения принимают переменные в различных случаях. Построение схемы позволяет увидеть логическую структуру выражения, а также выделить основные элементы и операции, выполняемые над ними.
Например, рассмотрим логическое выражение "A ИЛИ (B И НЕ C)". Для построения схемы этого выражения мы можем использовать прямоугольники для обозначения переменных (A, B и C) и линии для обозначения логических операторов (ИЛИ и НЕ). В результате получится наглядное представление выражения, где можно увидеть связи между переменными и выполняемыми операциями.
Построение схемы логического выражения может быть полезным для различных целей, включая разработку программного обеспечения, проектирование цифровых схем, анализ алгоритмов и решение логических задач. Этот подробный руководство с примерами поможет вам разобраться в процессе построения схемы логического выражения шаг за шагом и использовать ее в повседневной практике.
Построение схемы логического выражения

Для построения схемы логического выражения необходимо разбить его на отдельные логические операции и связать их между собой. Операторы И, ИЛИ и НЕ являются основными в логике и используются для объединения, разделения или инверсии логических значений.
Процесс построения схемы начинается с установления основного оператора, который определяет основное связывание между значениями. Затем следует определить компоненты выражения и связи между ними. В завершении схемы присваиваются значимые имена каждой компоненте, чтобы облегчить их понимание и использование в дальнейшем.
Давайте рассмотрим пример. Пусть у нас есть логическое выражение: "Если сегодня суббота и я не работаю, то я отдыхаю". Для начала определим основную операцию, которая будет использоваться для связи компонентов этого выражения. В данном случае это оператор ИЛИ.
Теперь выделим компоненты выражения: "сегодня суббота", "я не работаю" и "я отдыхаю". Установим связи между ними с помощью оператора ИЛИ. Таким образом, схема логического выражения будет выглядеть следующим образом:
Сегодня суббота Я не работаю Я отдыхаю | | | | | | | | | +-------ИЛИ--------+ | | | | |
По этой схеме можно легко понять, что для того, чтобы я отдыхал, необходимо, чтобы сегодня была суббота и я не работал. Если хотя бы одно из этих условий не выполняется, то я не отдыхаю.
Построение схемы логического выражения позволяет упростить его анализ и решение задач. Также схема помогает лучше понять структуру и связи компонентов выражения.
Понятие логического выражения

Оно может включать в себя различные операторы, такие как "И" (AND), "ИЛИ" (OR), "НЕ" (NOT), а также операторы сравнения, например "РАВНО" (=), "БОЛЬШЕ" (>), "МЕНЬШЕ" (
Логическое выражение может быть использовано для принятия решений в программировании, логических задачах или при работе с базами данных.
Пример логического выражения: Если x больше 5 и y меньше 10, то выражение истинно.
В данном примере "x > 5" и "y
Важно заметить, что логические выражения могут быть составными и содержать скобки для установления приоритета операций.
Знание понятия логического выражения является необходимым для правильного построения схемы логического выражения и использования его в решении конкретных задач.
Как правильно построить схему логического выражения
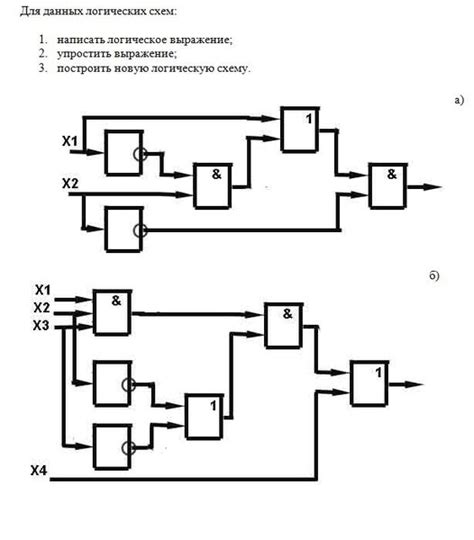
Для правильного построения схемы логического выражения следует следующие шаги:
- Определить переменные: каждая переменная в логическом выражении должна быть представлена символом или буквой. Например, "A", "B" и "C".
- Разбить выражение на части: выражение может быть разбито на отдельные компоненты, например, отдельные предложения или утверждения. Например, "A AND B" и "A OR C".
- Построить логическую структуру: используя символы, такие как стрелки или линии, свяжите переменные и компоненты логического выражения в соответствии с их взаимосвязью. Например, "A AND B" может быть представлено в виде стрелки, связывающей "A" и "B".
- Обозначить операторы: используя символы, такие как "AND", "OR" или "NOT", обозначьте операторы, которые связывают компоненты логического выражения. Например, "A AND B" может быть обозначено символом "&".
- Добавить логические значения: укажите истинность или ложность каждой переменной или компонента логического выражения. Например, "A = true" или "B = false".
Пример схемы логического выражения:
- Переменные:
- A = true
- B = false
- C = true
- Компоненты:
- "A AND B"
- "B OR C"
- Структура:
- Стрелка, связывающая "A" и "B" для "A AND B"
- Стрелка, связывающая "B" и "C" для "B OR C"
- Операторы:
- "AND" обозначено символом "&"
- "OR" обозначено символом "∨"
Создание схемы логического выражения позволяет с легкостью анализировать его структуру и взаимосвязи между компонентами. Это полезное инструмент для работы с сложными логическими выражениями и помогает в их понимании.
Пример построения схемы логического выражения
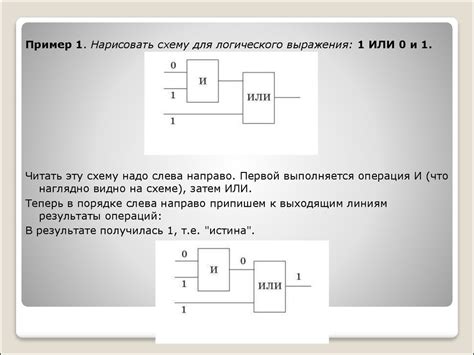
Построение схемы логического выражения может быть полезным при анализе и понимании сложных логических связей. Давайте рассмотрим пример, чтобы лучше понять, как это делается.
Предположим, у нас есть логическое выражение: "Если сегодня суббота или воскресенье и погода хорошая, то я пойду на прогулку". Давайте построим схему этого выражения.
На первом уровне схемы мы можем выделить два условия: "сегодня суббота или воскресенье" и "погода хорошая". Они будут составлять основные ветви схемы.
На втором уровне мы можем использовать символы "и" и "или" для объединения условий. Первое условие будет состоять из двух вариантов: "сегодня суббота" и "сегодня воскресенье". Второе условие, "погода хорошая", останется без изменений.
Таким образом, схема будет иметь следующий вид:
- Если
- Сегодня суббота
- Или
- Сегодня воскресенье
- И
- Погода хорошая
- То я пойду на прогулку
Это простой пример, но он демонстрирует основной принцип построения схемы логического выражения. Обратите внимание, что при построении схемы мы разбиваем сложное выражение на более простые условия, чтобы лучше его понять.
Таким образом, построение схемы логического выражения является полезным инструментом для анализа и понимания сложных логических связей.
Основные операторы логического выражения
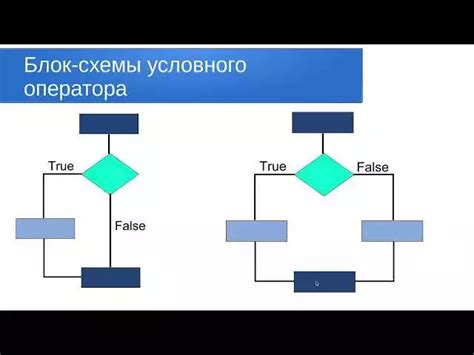
При построении схемы логического выражения необходимо использовать различные операторы для объединения и сравнения значений. В данном разделе рассмотрим основные операторы, которые можно использовать при построении логических выражений.
Операторы сравнения:
- == - оператор равенства, возвращает true, если значения двух операндов равны, иначе возвращает false.
- != - оператор неравенства, возвращает true, если значения двух операндов не равны, иначе возвращает false.
- > - оператор больше, возвращает true, если значение первого операнда больше значения второго операнда, иначе возвращает false.
- < - оператор меньше, возвращает true, если значение первого операнда меньше значения второго операнда, иначе возвращает false.
- >= - оператор больше или равно, возвращает true, если значение первого операнда больше или равно значению второго операнда, иначе возвращает false.
- <= - оператор меньше или равно, возвращает true, если значение первого операнда меньше или равно значению второго операнда, иначе возвращает false.
Операторы логического объединения:
- && - логическое "и", возвращает true, если оба операнда истинны, иначе возвращает false.