Комплексная плоскость – это система, в которой каждая точка представляет собой комбинацию из двух компонентов: вещественной и мнимой частей. Построение точек на комплексной плоскости является важным инструментом в математике и физике и позволяет визуализировать и исследовать различные математические и физические понятия.
Для построения точек на комплексной плоскости используется декартова система координат, где вещественная ось горизонтальная, а мнимая ось вертикальная. Каждая точка в комплексной плоскости имеет свои координаты на этой системе координат.
Для представления и работы с точками на комплексной плоскости используется специальный формат записи, который называется алгебраической формой. В этой форме точка представляется в виде a + bi, где a – это вещественная часть, а bi – это мнимая часть, умноженная на мнимую единицу i. Например, 3 + 2i представляет точку на комплексной плоскости с координатами (3, 2).
В данном руководстве мы рассмотрим несколько примеров построения точек на комплексной плоскости и объясним основные концепции и операции, связанные с этим процессом. Вы узнаете о сложении точек, умножении на число, а также о модуле и аргументе комплексных чисел. Все примеры будут сопровождаться подробными пояснениями, чтобы вы легко могли понять процесс построения и работу с точками на комплексной плоскости.
Построение точек на комплексной плоскости:
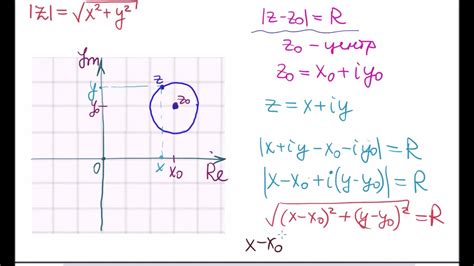
Комплексное число представляет собой комбинацию вещественной и мнимой частей. Вещественная часть определяет положение точки по оси x, а мнимая часть - по оси y.
Чтобы построить точку на комплексной плоскости, необходимо определить вещественную и мнимую части комплексного числа и разместить точку на соответствующих осях.
Например, рассмотрим комплексное число z = 3 + 2i. Вещественная часть этого числа равна 3, а мнимая часть - 2. Мы размещаем точку на координатах (3, 2) на комплексной плоскости.
Чтобы визуализировать комплексное число на комплексной плоскости, можно использовать стрелку или точку с маркером. Стрелка указывает направление и длину вектора, который соответствует комплексному числу, а точка определяет конкретную позицию числа на плоскости.
Построение точек на комплексной плоскости полезно при работе с комплексными числами и решении математических задач. Оно помогает визуализировать и понять свойства и взаимодействие комплексных чисел.
Используя это руководство и примеры, вы сможете научиться построению точек на комплексной плоскости и расширить свои знания об алгебре комплексных чисел.
Определение и примеры

Примеры точек на комплексной плоскости:
- Точка (0, 0) соответствует нулевому комплексному числу z = 0 + 0i.
- Точка (1, 0) соответствует действительному числу z = 1 + 0i.
- Точка (0, 1) соответствует мнимому числу z = 0 + 1i.
- Точка (-1, 0) соответствует действительному числу z = -1 + 0i.
- Точка (0, -1) соответствует мнимому числу z = 0 - 1i.
Комплексные числа, представленные точками на комплексной плоскости, могут быть использованы для моделирования и решения различных задач. Например, тригонометрические функции, такие как синус (sin) и косинус (cos), могут быть определены и вычислены с использованием комплексных чисел.
Работа с вещественными и мнимыми числами

На комплексной плоскости точки представлены в виде чисел комплексной плоскости. Комплексное число состоит из вещественной и мнимой частей.
Вещественное число представляет действительное значение на оси x, в то время как мнимое число представляет значение на оси y. На комплексной плоскости точка является координатой (x, y), где x - вещественная часть, а y - мнимая часть комплексного числа.
Работа с вещественными и мнимыми числами позволяет нам строить точки на комплексной плоскости и выполнять различные математические операции с комплексными числами.
Когда мы работаем с комплексными числами, важно понимать и учитывать их вещественную и мнимую составляющие. Вещественная и мнимая части могут быть положительными или отрицательными.
| Комплексное число | Вещественная часть | Мнимая часть |
|---|---|---|
| x + yi | x | y |
На практике мы можем работать с комплексными числами, используя ряд математических операций, таких как сложение, вычитание, умножение и деление.
Математические операции с комплексными числами выполняются по аналогии с обычными числами. Например, сложение двух комплексных чисел будет состоять из сложения их вещественных и мнимых частей.
Также мы можем представить комплексные числа в другой форме, называемой показательной формой. Она представляет число в виде r * e^(i * θ), где r - модуль комплексного числа, а θ - аргумент комплексного числа.
Работа с вещественными и мнимыми числами является важной составляющей построения точек на комплексной плоскости. Она позволяет нам лучше понять и использовать комплексные числа в геометрическом контексте.
Графическое представление точек на комплексной плоскости

Для графического представления комплексного числа на комплексной плоскости используется декартова система координат. В декартовой системе координат комплексная плоскость разделяется на две оси - вещественную ось (ось абсцисс) и мнимую ось (ось ординат).
Каждое комплексное число представляется в виде точки на комплексной плоскости, где вещественная часть числа определяет положение точки по оси абсцисс, а мнимая часть - положение точки по оси ординат. Таким образом, комплексное число z=a+bi на комплексной плоскости будет представлено точкой с координатами (a, b).
Графическое представление точек на комплексной плоскости позволяет наглядно представить операции над комплексными числами, такие как сложение, вычитание, умножение и деление. Например, сложение двух комплексных чисел a+b и c+d представляет собой сдвиг точки a+b на вектор с концом в точке c+d. Аналогично, вычитание и умножение комплексных чисел также имеют свое графическое представление.
Графическое представление точек на комплексной плоскости также позволяет наглядно представить геометрические свойства комплексных чисел, такие как модуль и аргумент. Модуль комплексного числа представляет собой расстояние от начала координат до точки на комплексной плоскости, соответствующей данному числу. Аргумент комплексного числа представляет собой угол между положительным направлением вещественной оси и лучом, исходящим из начала координат и проходящим через данную точку.
Использование графического представления точек на комплексной плоскости значительно упрощает работу с комплексными числами, позволяя наглядно представить различные операции и свойства. Поэтому понимание работы с комплексными числами на комплексной плоскости является необходимым навыком в математике и его изучение рекомендуется всем, интересующимся этой областью знаний.
Координаты и модуль комплексных чисел
Комплексные числа можно представить на комплексной плоскости, где действительная часть откладывается вдоль оси x, а мнимая часть – вдоль оси y. Точка на комплексной плоскости, соответствующая комплексному числу a + bi, будет иметь координаты (a, b).
Модуль комплексного числа определяется как расстояние от начала координат до соответствующей точки на комплексной плоскости. Модуль комплексного числа a + bi обозначается как |a + bi| и вычисляется по формуле:
|a + bi| = √(a2 + b2)
Модуль комплексного числа представляет собой длину вектора, соединяющего начало координат и точку на комплексной плоскости.
Знание координат и модуля комплексных чисел является важным для понимания и использования комплексной арифметики и геометрии.
Сложение и умножение точек в комплексной плоскости
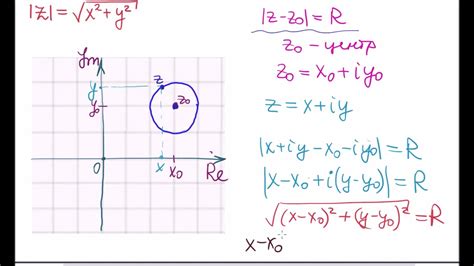
Сложение двух точек в комплексной плоскости проводится путем сложения их комплексных чисел. Пусть даны две точки: z1 = x1 + iy1 и z2 = x2 + iy2. Их сумма будет z1 + z2 = (x1 + x2) + i(y1 + y2).
Умножение двух точек также выполняется путем умножения их комплексных чисел. Если z1 = x1 + iy1 и z2 = x2 + iy2, их произведение будет z1 * z2 = (x1 * x2 - y1 * y2) + i(x1 * y2 + x2 * y1).
Можно представить сложение и умножение точек в комплексной плоскости графически. Сумма двух точек будет равна векторной сумме их координат, и произведение будет приводить к изменению модуля и аргумента исходных точек.
Сложение и умножение точек в комплексной плоскости широко используются в математике, физике, технике и других областях. Они позволяют выполнять различные операции с векторами и решать сложные задачи геометрии и алгебры.
Практическое применение в физике и технике

| Приложение | Примеры |
| Электрические цепи | Комплексное представление элементов схемы в виде импедансов позволяет анализировать и проектировать сложные электрические цепи. Благодаря построению точек на комплексной плоскости можно моделировать перемещение энергии, рассчитывать частотные характеристики и оптимизировать работу системы. |
| Активные фильтры | Для проектирования и анализа активных фильтров (например, фильтров Баттерворта или Чебышева) алгоритмы построения точек на комплексной плоскости позволяют определить положение полюсов и нулей передаточной функции, что важно для достижения заданных частотных характеристик. |
| Управление системами | В задачах управления и автоматизации систем используется аппарат комплексных переменных, позволяющий учесть не только амплитуду, но и фазовые характеристики и устойчивость системы. Построение точек на комплексной плоскости является неотъемлемой частью анализа и разработки систем управления. |
| Сигнальная обработка | Комплексные числа применяются для анализа и обработки сигналов, таких как звуковые или электрические сигналы. Построение точек на комплексной плоскости позволяет проводить фурье-преобразование и анализировать спектральные характеристики сигнала. |
Это лишь небольшой набор примеров практического применения построения точек на комплексной плоскости. В реальности такие методы используются в различных областях, от электротехники до экономики. Построение точек на комплексной плоскости является мощным инструментом, который помогает моделировать и анализировать сложные системы, а также находить оптимальные решения в реальных задачах.