Построение точек на трехмерной координатной плоскости является важным аспектом визуализации и анализа пространственных данных. Это позволяет визуально представить расположение объектов в трехмерном пространстве и проводить различные геометрические и статистические операции.
Для начинающих может показаться сложным задачей построение точек в трехмерном пространстве. Однако, с помощью правильного руководства и примеров, вы сможете с легкостью освоить этот навык. В этой статье мы рассмотрим основные принципы построения точек на трехмерной координатной плоскости и предоставим вам подробный гайд.
Прежде чем перейти к построению точек, важно понять основные компоненты трехмерной координатной плоскости. В трехмерном пространстве каждая точка определяется тремя координатами: x, y и z. Координаты x и y представляют горизонтальные плоскости, а координата z обозначает вертикальную ось. При задании координат точки в трехмерном пространстве, используется следующий формат: (x, y, z). Например, точка с координатами (3, 2, 1) находится на расстоянии 3 единицы от начала горизонтальной оси, 2 единицы от начала вертикальной оси и 1 единицу от начала глубинной оси.
Построение точки на трехмерной координатной плоскости

В трехмерной геометрии точка определяется координатами по трем осям: X, Y и Z. Построение точки на трехмерной координатной плоскости может быть осуществлено с помощью таблицы, в которой указываются значения координат точки.
Ниже приведен пример таблицы, демонстрирующей построение точки с координатами (x, y, z):
| X | Y | Z |
|---|---|---|
| 2 | 3 | 4 |
В данном примере точка имеет координаты (2, 3, 4) и будет находиться на трехмерной координатной плоскости в соответствующих обозначенных значениях осей X, Y и Z.
Для построения точки на трехмерной координатной плоскости также может использоваться графический редактор или специализированный программный инструмент. Однако, при использовании таблицы с явным указанием координат, процесс построения можно выполнить вручную.
Руководство по построению точки на трехмерной координатной плоскости

Шаги для построения точки на трехмерной координатной плоскости:
- Определите систему координат. Трехмерная координатная плоскость имеет три орта: ось X, ось Y и ось Z. Ось X обычно направлена вправо, ось Y - вверх, а ось Z - навстречу наблюдателю.
- Задайте координаты точки. Координаты точки представляют собой уникальные числа, определяющие положение точки в трехмерном пространстве. Обычно координаты обозначаются как (X, Y, Z). Например, точка с координатами (1, 2, 3) находится на оси X в точке с координатой 1, на оси Y в точке с координатой 2 и на оси Z в точке с координатой 3.
- Постройте точку на трехмерной координатной плоскости. Для этого сначала проведите перпендикуляры от координатных осей к соответствующим координатам точки, а затем пересечение этих перпендикуляров будет точкой на плоскости.
Пример построения точки на трехмерной координатной плоскости:
Допустим, нам дана точка с координатами (2, 3, 4).
- Установим систему координат. Ось X будет направлена вправо, ось Y - вверх, а ось Z - навстречу наблюдателю.
- Найдем координаты точки. Координаты точки: X = 2, Y = 3, Z = 4.
- Проведем перпендикуляры от координатных осей к соответствующим координатам точки. Перпендикуляры должны пересекаться в одной точке.
- Пересечение перпендикуляров будет точкой на трехмерной координатной плоскости. В данном случае, точка будет находиться в координатах (2, 3, 4).
Таким образом, построение точки на трехмерной координатной плоскости требует определения системы координат, задания координат точки и проведения перпендикуляров от координатных осей к соответствующим координатам точки.
Примеры построения точки на трехмерной координатной плоскости
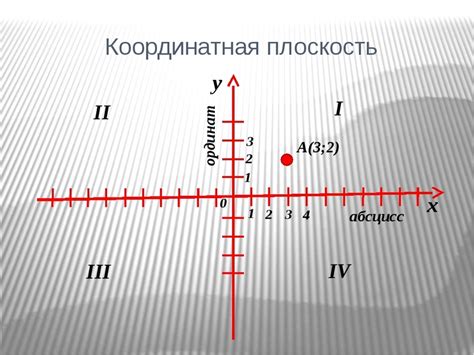
Для построения точки на трехмерной координатной плоскости необходимо знать ее координаты в виде трех чисел, представляющих собой значение по осям X, Y и Z.
Например, рассмотрим точку с координатами (2, 4, -3). Для ее построения нужно найти на плоскости оси X, Y и Z и отметить на них соответствующие значения.
На плоскости оси X, Y и Z будут представляться в виде трех взаимно перпендикулярных прямых, соответствующих каждой из осей. Ось X будет горизонтальной, ось Y - вертикальной, а ось Z - направленной вглубь плоскости.
Чтобы построить точку (2, 4, -3), находим на оси X значение 2, на оси Y - значение 4 и на оси Z - значение -3. Затем проводим прямые, проходящие через соответствующие значения на осях, и точка пересечения этих прямых будет искомой точкой.
Итак, точка (2, 4, -3) будет находиться на пересечении прямых, соответствующих значению 2 на оси X, значению 4 на оси Y и значению -3 на оси Z.
Таким образом, мы можем построить точку на трехмерной координатной плоскости, используя ее координаты в виде трех чисел.
Гайд для начинающих по построению точки на трехмерной координатной плоскости
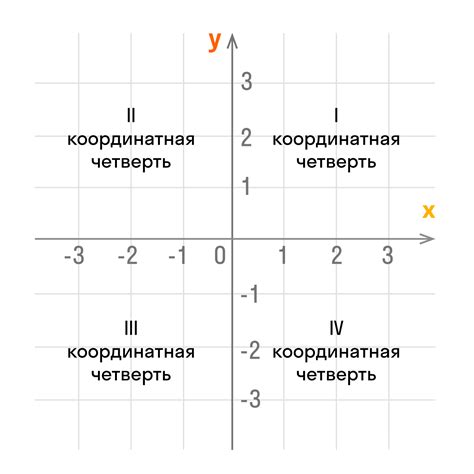
Для построения точек на трехмерной координатной плоскости нужно знать их координаты. В трехмерной системе координат точка обозначается кортежем чисел (x, y, z). x определяет положение точки по горизонтали, y - по вертикали, z - по глубине.
Чтобы визуализировать точку на трехмерной координатной плоскости, можно использовать графические программы или построить модель в виде геометрического объекта. Многие программы, такие как AutoCAD или Blender, предлагают возможность создавать трехмерные модели и расставлять точки на координатной плоскости.
Примером построения точки в трехмерной координатной плоскости может быть такая команда в языке программирования Python:
point = (1, 2, 3)
Это означает, что точка имеет координаты x = 1, y = 2 и z = 3. Используя аналогичные команды, можно создать и изменять точки в трехмерном пространстве.
Зная координаты точки, можно вычислить и другие параметры, такие как расстояние между точками или угол между векторами, используя соответствующие формулы и алгоритмы.
Построение точек на трехмерной координатной плоскости - важный элемент при работе с трехмерной графикой и моделировании. Поэтому необходимо хорошо понимать принципы работы с трехмерными координатами и уметь строить точки на трехмерной координатной плоскости.
Техники построения точки на трехмерной координатной плоскости для новичков

Построение точек на трехмерной координатной плоскости может показаться сложной задачей для начинающих. Однако с правильным подходом и руководством этот процесс станет легким и понятным.
Вначале необходимо определить значения координат x, y и z для точки, которую вы хотите построить. Обратите внимание, что в трехмерной координатной системе каждой точке соответствуют три значения координат.
Шаг 1: На трехмерной координатной плоскости найдите начало координат, которое обозначается точкой (0, 0, 0). Это место, где пересекаются оси x, y и z.
Шаг 2: Примите первое значение координаты x и найдите на оси x соответствующую ему точку. После этого проведите вертикальную линию вверх или вниз от точки на ось y до значения координаты y.
Шаг 3: Используйте значение координаты z для проведения горизонтальной линии из точки на прямую, представляющую значение координаты x и y. Это позволит вам найти точку в трехмерном пространстве.
Выполнив эти три шага для каждой точки, вы сможете построить трехмерную координатную систему и отобразить точки в ней. Помните, что координаты могут принимать положительные и отрицательные значения, а также могут быть равными нулю.
Вы можете использовать различные цвета или маркеры, чтобы выделить каждую точку и сделать графическое представление более наглядным.
Пример:
Построим точку с координатами (2, -3, 4).
1. Найдем начало координат, точку (0, 0, 0).
2. Переместимся вправо на 2 единицы по оси x и проведем вертикальную линию вниз на 3 единицы по оси y.
3. Из полученной точки проведем горизонтальную линию вправо на 4 единицы по оси z.
Таким образом, мы построили точку (2, -3, 4) на трехмерной координатной плоскости.
Важно отметить, что трехмерная координатная система может использоваться для визуализации объектов в пространстве, и точки могут представлять точки в трехмерном пространстве, как, например, вершины многогранных фигур или положение объектов в трехмерной модели.
Подробное руководство по построению точки на трехмерной координатной плоскости
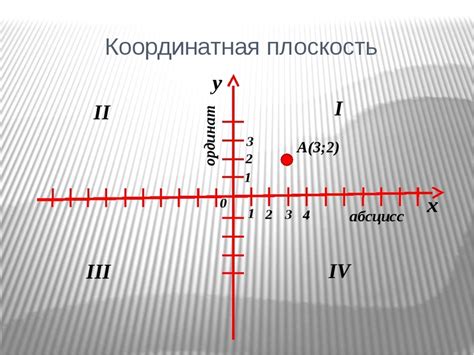
Построение точки на трехмерной координатной плоскости включает такие шаги:
- Определение системы координат.
- Назначение значений координат точки.
- Отметка точки на основе ее координат.
Давайте подробнее рассмотрим каждый из этих шагов.
1. Определение системы координат
Первым шагом в построении точки на трехмерной координатной плоскости является определение системы координат. Трехмерная координатная плоскость состоит из трех осей - x, y и z. Оси x и y расположены в горизонтальной плоскости, а ось z - в вертикальной плоскости и перпендикулярна плоскости x и y.
Оси имеют положительные и отрицательные направления. Положительное направление оси x идет вправо, оси y - вверх, а оси z - от нас вглубь плоскости.
На схеме трехмерной координатной плоскости ось x обычно располагается горизонтально, ось y - вертикально, а ось z - от нас вглубь изображения.
Координаты точек на трехмерной координатной плоскости записываются в форме (x, y, z), где x - координата точки по оси x, y - координата точки по оси y, z - координата точки по оси z.
2. Назначение значений координат точки
После определения системы координат необходимо назначить значения координат для точки, которую необходимо построить на трехмерной координатной плоскости. В зависимости от поставленной задачи, координаты точки могут быть положительными или отрицательными числами.
Можно использовать числовые данные или переменные для представления значений координат.
3. Отметка точки на основе ее координат
Когда значения координат точки определены, можно приступить к отметке точки на трехмерной координатной плоскости. Для этого нужно переместиться по осям x, y и z, чтобы найти место, соответствующее значениям координат точки.
Отметка точки обычно представляется в виде отрезка, точка которого соответствует заданным координатам. С помощью линейки или другого инструмента можно провести такой отрезок, чтобы визуально представить точку на плоскости.
По окончании этих трех шагов мы получим построенную точку на трехмерной координатной плоскости.
Построение точек на трехмерной координатной плоскости является важной задачей в геометрии и 3D-моделировании. Используя эти простые шаги, вы сможете точно и наглядно отображать точки на трехмерной плоскости и использовать их в дальнейшей работе.