Построение треугольника на оси является одной из основных задач геометрии. Для решения этой задачи важно уметь правильно расположить точки на оси и построить вокруг них треугольник. В данной статье будет рассмотрен метод построения треугольника на оси и его результаты.

Первым шагом при построении треугольника на оси является выбор двух точек на оси, которые будут являться вершинами треугольника. Затем необходимо определить третью точку, которая будет либо находиться на одной из осей, либо вне их. Для этого можно использовать различные математические формулы и правила.

После определения всех трех точек необходимо построить отрезки между ними, чтобы получить сам треугольник. Важно при этом помнить о корректном порядке вершин треугольника, чтобы избежать неправильного построения или перекрывания отрезков. В результате мы получим готовый треугольник на оси.

Построение треугольника на оси является важной задачей геометрии и может использоваться в различных сферах, таких как строительство, архитектура, программирование и другие. Используя данный метод и получив результат, можно решать различные задачи и проводить различные исследования на основе построенного треугольника.

Метод построения треугольника на оси

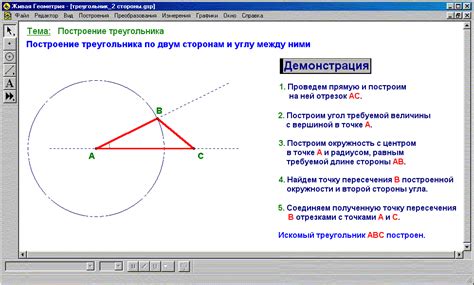
Для построения треугольника на оси нам необходимо знать координаты его вершин. Координата вершины A обозначается как (x1, y1), координата вершины B – (x2, y2), а координата вершины C – (x3, y3).

Используя эти координаты, мы можем вычислить длины сторон треугольника с помощью формулы расстояния между двумя точками на плоскости:

d = sqrt((x2 - x1)^2 + (y2 - y1)^2)

Зная длины сторон треугольника, мы можем вычислить его площадь по формуле Герона:

S = sqrt(p * (p - a) * (p - b) * (p - c))

где a, b и c – длины сторон треугольника, а p – полупериметр:

p = (a + b + c) / 2

Таким образом, метод построения треугольника на оси позволяет нам точно определить его положение в пространстве и вычислить его основные характеристики, такие как длины сторон и площадь.

Результат построения треугольника на оси

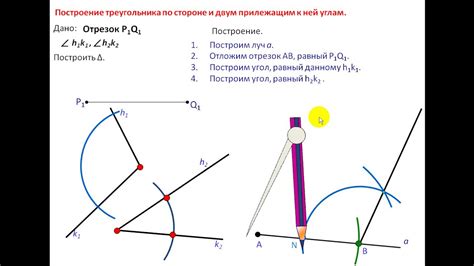
При построении треугольника на оси, каждая из трех точек может быть представлена как пара чисел (x, y). Координата x отображает положение точки по горизонтальной оси, а координата y - по вертикальной оси.

Используя эти координаты, можно легко определить длины сторон треугольника, а также его площадь и периметр. Кроме того, можно вычислить различные углы треугольника, используя тригонометрические функции.

Построение треугольника на оси также помогает в решении различных задач, связанных с геометрией и алгеброй. Это может быть использовано для построения графиков функций, определения взаимного расположения различных геометрических объектов, а также для решения систем уравнений и поиска точек пересечения.

В целом, построение треугольника на оси предоставляет нам мощный инструмент для визуализации и анализа различных геометрических задач. Знание этого метода и его результатов может быть полезно во многих практических ситуациях.