Построение треугольника по координатам вершин является одной из важных задач в компьютерной графике и геометрии. Треугольники широко используются для визуализации геометрических объектов, создания анимаций, моделирования физических процессов и многого другого. В данной статье мы рассмотрим различные методы и алгоритмы, которые позволяют по заданным координатам вершин построить треугольник.

Существует несколько основных методов построения треугольника по координатам вершин. Один из самых простых и понятных методов - метод соединения отдельных отрезков между точками вершин. С помощью этого метода мы можем построить треугольник, соединяя каждую вершину с каждой остальной вершиной отрезками. Этот метод достаточно простой и понятный для понимания, однако он имеет некоторые ограничения и не всегда удобен в использовании.

Еще одним распространенным методом построения треугольника является метод определения углов и длин сторон треугольника на основе координат вершин. Для этого необходимо использовать тригонометрические функции, такие как синус, косинус и тангенс. Этот метод позволяет точно вычислить углы и длины сторон треугольника на основе заданных координат вершин. Он более гибкий и универсальный, но требует больше вычислительных ресурсов и может быть сложным для понимания для некоторых людей.

Методы и алгоритмы для построения треугольника по координатам вершин

Один из наиболее распространенных методов - это метод определителей. Он основан на использовании определителей матриц и матричных операций. Сначала необходимо определить коэффициенты уравнений прямых, проходящих через каждую пару вершин треугольника. Затем, используя определители матриц, можно вычислить площадь треугольника. Если площадь равна нулю, то вершины лежат на одной прямой и треугольник не существует.

Другой метод - это метод векторных произведений. Он основан на свойствах векторного произведения и позволяет найти нормаль к плоскости, в которой лежит треугольник. С помощью векторных произведений можно найти вектора, соединяющие вершины треугольника, и вычислить их векторное произведение. Если векторное произведение равно нулю, значит вершины лежат на одной прямой и треугольник не существует.

Также существуют и другие методы, например, метод использования углов. С его помощью можно вычислить углы треугольника, используя формулы тригонометрии и координаты вершин. Если сумма углов равна 180 градусов, то треугольник существует.

Таким образом, для построения треугольника по координатам его вершин существуют различные методы и алгоритмы, которые можно выбирать в зависимости от конкретной ситуации и задачи. Каждый из этих методов имеет свои особенности и применяется в различных областях математики и компьютерной графики.

Построение треугольника по координатам вершин: инструкция и примеры

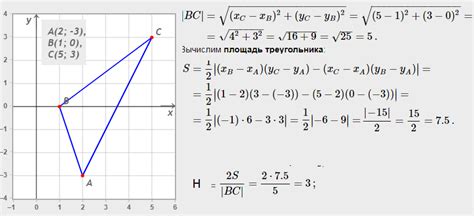
Для начала необходимо задать координаты трех вершин треугольника: A(x1, y1), B(x2, y2) и C(x3, y3). На основе этих координат можно вычислить длины сторон треугольника, используя формулу расстояния между двумя точками в пространстве:

d = sqrt((x2 - x1)^2 + (y2 - y1)^2)

После определения длин трех сторон треугольника, можно найти его площадь с помощью формулы Герона:

S = sqrt(p * (p - a) * (p - b) * (p - c)), где p = (a + b + c) / 2

Также можно вычислить углы треугольника, используя законы косинусов и синусов:

cosA = (b^2 + c^2 - a^2) / (2 * b * c)

cosB = (a^2 + c^2 - b^2) / (2 * a * c)

cosC = (a^2 + b^2 - c^2) / (2 * a * b)

Углы можно найти с помощью обратной функции арккосинуса:

A = arccos(cosA)

B = arccos(cosB)

C = arccos(cosC)

Таким образом, зная координаты вершин треугольника, можно вычислить его характеристики, такие как длины сторон, площадь и углы. Эти данные могут быть использованы для различных целей, например, для построения треугольника на плоскости или решения геометрических задач.

Пример:

Пусть заданы следующие координаты трех вершин треугольника:

A(0, 0)

B(3, 0)

C(0, 4)

Вычислим длины сторон треугольника:

AB = sqrt((3 - 0)^2 + (0 - 0)^2) = 3

BC = sqrt((0 - 3)^2 + (4 - 0)^2) = 5

AC = sqrt((0 - 0)^2 + (4 - 0)^2) = 4

Вычислим площадь треугольника:

p = (3 + 5 + 4) / 2 = 6

S = sqrt(6 * (6 - 3) * (6 - 5) * (6 - 4)) = 6

Вычислим углы треугольника:

cosA = (5^2 + 4^2 - 3^2) / (2 * 5 * 4) = 0.25

cosB = (3^2 + 5^2 - 4^2) / (2 * 3 * 5) = 0.4

cosC = (3^2 + 4^2 - 5^2) / (2 * 3 * 4) = 0.072

A = arccos(0.25) ≈ 75.52°

B = arccos(0.4) ≈ 66.42°

C = arccos(0.072) ≈ 38.06°

Таким образом, треугольник АВС имеет длины сторон: AB = 3, BC = 5, AC = 4. Площадь треугольника равна 6, а углы А, В и С примерно равны 75.52°, 66.42° и 38.06° соответственно.