Построение треугольника - важная задача, с которой сталкиваются многие программисты, разрабатывающие графические приложения. В этой статье мы рассмотрим подробную инструкцию по построению треугольника с помощью программного кода.
Первым шагом при построении треугольника является выбор языка программирования и графической библиотеки. Для данной инструкции мы будем использовать язык программирования C++ и графическую библиотеку OpenGL. Однако, алгоритмы и принципы, которые мы рассмотрим, применимы к любому языку программирования и графической библиотеке.
Для начала работы с построением треугольника необходимо подключить необходимые библиотеки и определить основные параметры, такие как размеры окна и цвет фона. Далее следует инициализация графического контекста и создание объекта треугольника.
Объект треугольника в программе представляется с помощью массива, содержащего вершины треугольника. Каждая вершина определяется тремя координатами - x, y и z, которые задают положение точки в трехмерном пространстве. После создания объекта треугольника, его необходимо отобразить на экране с помощью метода рендеринга. В данной инструкции мы будем использовать метод рендеринга OpenGL, который позволяет создавать трехмерные изображения и анимацию.
Построение треугольника в программе: шаг за шагом
- Определить, какую библиотеку или фреймворк вы хотите использовать для построения треугольника. Например, вы можете использовать библиотеку SVG или Canvas в JavaScript.
- Создать объект треугольника, используя функции или методы выбранной библиотеки или фреймворка. Некоторые из этих функций могут включать методы для определения координат вершин треугольника или методы для рисования треугольника на экране.
- Определить параметры треугольника, такие как длины сторон и углы. Вы можете использовать переменные для хранения этих параметров и передавать их в соответствующую функцию или метод.
- Используйте указанные функции или методы, чтобы нарисовать треугольник на экране с использованием заданных параметров. Например, вы можете вызвать функцию "рисования треугольника" и передать ей значения параметров треугольника.
- Проверьте код на предмет ошибок и запустите программу, чтобы увидеть на экране нарисованный треугольник.
Это основные шаги для построения треугольника в программе. Они могут быть дополнены или изменены в зависимости от выбранной библиотеки или фреймворка для рисования треугольника.
Инструменты и язык программирования

Для построения треугольника в программе можно использовать различные инструменты и языки программирования. В зависимости от ваших навыков и предпочтений, вы можете выбрать наиболее подходящий вариант.
Один из самых популярных языков программирования для создания графических приложений - это Python. С помощью библиотеки Tkinter, вы можете легко создать окно приложения и нарисовать треугольник на экране. Пример кода на Python:
import tkinter as tk def draw_triangle(canvas, x1, y1, x2, y2, x3, y3): canvas.create_polygon(x1, y1, x2, y2, x3, y3) def main(): window = tk.Tk() canvas = tk.Canvas(window, width=400, height=400) canvas.pack() # Координаты вершин треугольника x1, y1 = 100, 100 x2, y2 = 200, 300 x3, y3 = 300, 100 draw_triangle(canvas, x1, y1, x2, y2, x3, y3) window.mainloop() if __name__ == "__main__": main()
Если вы предпочитаете веб-технологии, то можно использовать язык программирования JavaScript и библиотеку для работы с графикой, например, Canvas. Пример кода на JavaScript:
function drawTriangle() {
var canvas = document.getElementById("myCanvas");
var ctx = canvas.getContext("2d");
// Координаты вершин треугольника
var x1 = 100, y1 = 100;
var x2 = 200, y2 = 300;
var x3 = 300, y3 = 100;
ctx.beginPath();
ctx.moveTo(x1, y1);
ctx.lineTo(x2, y2);
ctx.lineTo(x3, y3);
ctx.closePath();
ctx.fill();
}
window.onload = function() {
drawTriangle();
};
Кроме того, существует множество других инструментов и языков программирования, которые можно использовать для построения треугольников в программе. Пожалуйста, выберите наиболее подходящий для вас и начните творить!
Определение типа треугольника
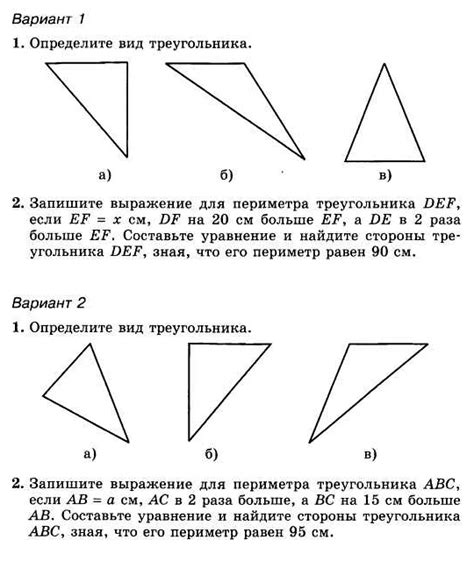
После построения треугольника в программе, можно определить его тип. Для этого можно использовать следующий алгоритм:
- Используйте формулу для вычисления длин сторон треугольника.
- Сравните полученные значения длин сторон треугольника.
- Если все три стороны равны, то треугольник является равносторонним.
- Если две стороны равны, а третья отличается, то треугольник является равнобедренным.
- Если все три стороны различны, то треугольник является разносторонним.
- Если сумма квадратов двух меньших сторон не равна квадрату самой большой стороны, то треугольник не существует.
- Если сумма квадратов двух меньших сторон равна квадрату самой большой стороны, то треугольник является прямоугольным.
Определение типа треугольника в программе является важным шагом, который позволяет дополнительно анализировать его свойства и использовать в дальнейших расчетах.
Вычисление периметра треугольника
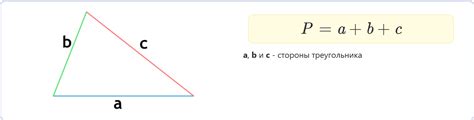
Если длины сторон треугольника известны, то периметр можно найти путем сложения этих длин:
Периметр треугольника = длина стороны AB + длина стороны BC + длина стороны CA
Например, если длины сторон треугольника равны AB = 3, BC = 4 и CA = 5, то периметр треугольника будет:
Периметр треугольника = 3 + 4 + 5 = 12
Таким образом, периметр треугольника с длинами сторон AB = 3, BC = 4 и CA = 5 равен 12.
Нахождение площади треугольника
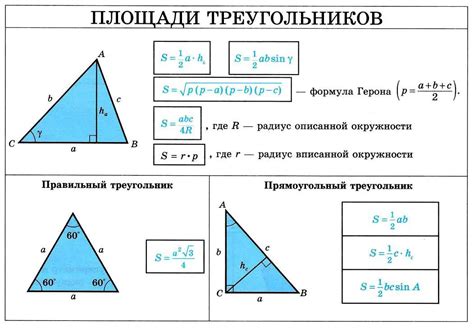
Площадь треугольника можно найти различными способами, в зависимости от известных данных. Вот несколько простых методов:
1. Площадь треугольника по формуле Герона:
Если известны длины всех трех сторон треугольника (a, b, c), то площадь можно найти по формуле Герона:
S = √(p * (p - a) * (p - b) * (p - c))
где p - полупериметр треугольника, вычисляемый по формуле p = (a + b + c) / 2.
2. Площадь треугольника по базованию и высоте:
Если известны длина базы треугольника (b) и его высота (h), то площадь можно найти по формуле:
S = (b * h) / 2
3. Площадь треугольника по координатам вершин:
Если известны координаты вершин треугольника (x1, y1), (x2, y2) и (x3, y3), то площадь можно найти по формуле:
S = 0.5 * |(x1 * (y2 - y3) + x2 * (y3 - y1) + x3 * (y1 - y2))|
где |x| - модуль числа x.
Выберите метод, который подходит к вашей ситуации и вычислите площадь треугольника, используя соответствующую формулу.
Построение треугольника на графическом экране
Вот пример простого кода на языке программирования C++ с использованием библиотеки OpenGL, который позволяет построить треугольник на графическом экране:
#include <GL/glut.h>
// Функция отрисовки
void renderScene() {
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glBegin(GL_TRIANGLES);
glVertex3f(-0.5, -0.5, 0.0);
glVertex3f(0.5, -0.5, 0.0);
glVertex3f(0.0, 0.5, 0.0);
glEnd();
glutSwapBuffers();
}
int main(int argc, char **argv) {
// Инициализация GLUT и создание окна
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DEPTH | GLUT_DOUBLE | GLUT_RGBA);
glutInitWindowPosition(100, 100);
glutInitWindowSize(320, 320);
glutCreateWindow("Треугольник");
// Регистрация функции отрисовки
glutDisplayFunc(renderScene);
// Основной цикл GLUT
glutMainLoop();
return 0;
}
В данном примере мы используем функцию glBegin(GL_TRIANGLES) для определения начала рисования треугольника. Затем мы указываем координаты каждой из трех вершин треугольника с помощью функции glVertex3f(x, y, z). В данном случае треугольник имеет вершины (-0.5, -0.5, 0.0), (0.5, -0.5, 0.0) и (0.0, 0.5, 0.0).
Затем мы инициализируем GLUT с помощью функции glutInit() и создаем окно, задав его размер и положение на экране с помощью функций glutInitWindowSize() и glutInitWindowPosition(). Мы также регистрируем функцию renderScene() как функцию отрисовки, которая будет вызываться GLUT для отображения содержимого окна. Затем мы входим в основной цикл GLUT с помощью функции glutMainLoop(), который обрабатывает все события окна и вызывает соответствующие функции для их обработки.
Пример программы для построения треугольника
Ниже приведен пример программы на языке Python, которая позволяет построить треугольник с заданными сторонами:
- Сначала необходимо импортировать модуль math, чтобы воспользоваться его функцией sqrt для вычисления квадратного корня.
- Затем пользователю предлагается ввести длины сторон треугольника.
- Следующим шагом программа проверяет, существует ли треугольник с заданными сторонами.
- Если треугольник существует, программа вычисляет его площадь и периметр.
Вот код программы:
import math
# Ввод длин сторон треугольника
a = float(input("Введите длину стороны A: "))
b = float(input("Введите длину стороны B: "))
c = float(input("Введите длину стороны C: "))
# Проверка существования треугольника
if a + b > c and a + c > b and b + c > a:
# Вычисление площади по формуле Герона
p = (a + b + c) / 2
area = math.sqrt(p * (p - a) * (p - b) * (p - c))
# Вычисление периметра
perimeter = a + b + c
print("Площадь треугольника:", area)
print("Периметр треугольника:", perimeter)
else:
print("Треугольник с заданными сторонами не существует.")