Равнобедренный треугольник – это такой треугольник, у которого две стороны равны между собой. Как известно, в равнобедренном треугольнике высота – это отрезок, проходящий через вершину и перпендикулярный основанию. Можно ли построить такую высоту с помощью обычного циркуля? Давайте разберемся вместе!
Для начала стоит отметить, что высота в равнобедренном треугольнике всегда будет пересекать основание точно по середине. Это свойство равнобедренных треугольников помогает нам в построении высоты с помощью циркуля.
Для построения высоты берем циркуль и делаем отметку на основании треугольника – прямой стороне, которая не является равной его сторонам. Затем, не изменяя расстояния на циркуле, ставим его ножки на вершину треугольника и начинаем рисовать дугу, которая пересечет основание. Мы завершаем построение высоты, когда дуга пересекает основание точно по середине.
Значение и построение высоты в равнобедренном треугольнике
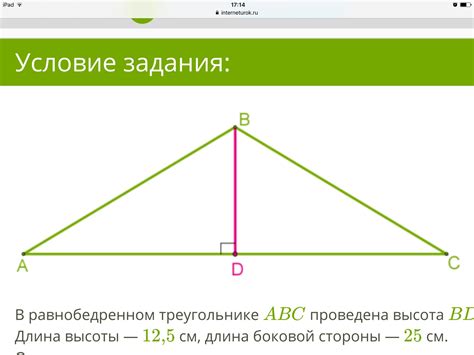
Высота равнобедренного треугольника - это отрезок, опущенный из вершины до основания, перпендикулярно к основанию треугольника. Высота разделяет основание на две равные части.
Значение высоты в равнобедренном треугольнике зависит от длины его основания и высоты, на которой он построен. Высота равнобедренного треугольника является биссектрисой в вершину этого треугольника и восходящей медианой своего основания. Длина высоты можно вычислить с помощью различных формул, таких как формула Герона или формула полупериметра.
Построение высоты в равнобедренном треугольнике с помощью циркуля можно выполнить следующим образом:
- Выберите любую сторону треугольника и отметьте ее середину.
- Установите в циркуле радиус, равный расстоянию от середины стороны до вершины равнобедренного треугольника.
- Опишите дугу из середины стороны треугольника, пересекающую обе боковые стороны треугольника.
- Отметьте точку пересечения дуги с боковой стороной.
- Продолжите отмечать точки пересечения смежных боковых сторон таким образом, пока не достигнете основания треугольника.
- Проведите отмеченные точки до вершины равнобедренного треугольника. Полученная линия будет являться высотой треугольника.
Построение высоты в равнобедренном треугольнике с помощью циркуля позволяет удобно и точно определить значение высоты и использовать его в дальнейших вычислениях и конструкциях.
Основные понятия и свойства

- Равнобедренный треугольник - это треугольник, у которого два из трех его сторон и два из трех его углов равны между собой.
- Высота треугольника - это отрезок, проведенный из вершины треугольника к основанию, перпендикулярно к соответствующей стороне.
- База треугольника - это наибольшая из двух равных сторон треугольника, на которую опирается высота.
- Серединный перпендикуляр – это прямая, проходящая через середину стороны треугольника и перпендикулярная к этой стороне.
- Точка пересечения высот треугольника - это точка, в которой пересекаются все высоты треугольника.
Построение высоты равнобедренного треугольника с помощью циркуля сводится к построению серединной перпендикуляра к его основанию. Построение осуществляется следующим образом:
- С помощью компаса снимите на основании треугольника два одинаковых отрезка, равных половине его длины.
- Прокладывая дуги с центрами в обоих концах основания, проведите линию, соединяющую точки пересечения этих дуг.
- Получившаяся линия является серединным перпендикуляром к основанию и, следовательно, является высотой равнобедренного треугольника.
Таким образом, построение высоты в равнобедренном треугольнике с помощью циркуля является простым и эффективным способом получить требуемый результат.
Использование циркуля для построения высоты
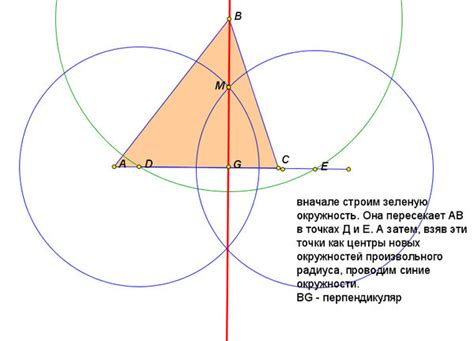
- Выберите вершину треугольника и назовите ее "A".
- Возьмите циркуль и установите его точку на вершине "A".
- Откройте циркуль на расстояние, большее половины основания треугольника.
- Проведите дугу циркулем, которая пересекает стороны треугольника в двух точках. Назовите эти точки "B" и "C".
- Соедините точку "A" с точкой "B" и точку "A" с точкой "C" с помощью линейки. Эти отрезки будут сторонами треугольника и базой для построения высоты.
- Возьмите циркуль и установите его точку на точке "B" или "C".
- Откройте циркуль на любое расстояние.
- Проведите дугу циркулем, которая пересекает сторону треугольника в одной точке. Назовите эту точку "D".
- Соедините точку "D" с вершиной треугольника "A". Этот отрезок будет высотой треугольника.
Теперь вы можете использовать циркуль и линейку для построения высоты в равнобедренном треугольнике, чтобы измерить ее длину или выполнить другие расчеты, связанные с треугольником.
Шаги построения высоты с помощью циркуля
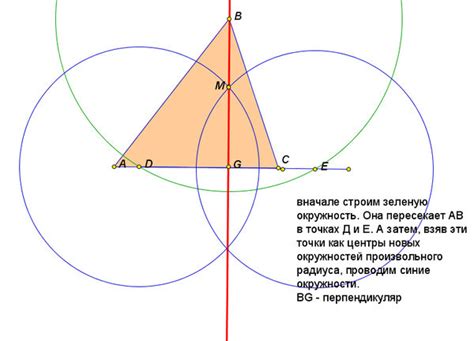
Для построения высоты в равнобедренном треугольнике с помощью циркуля следуйте следующим шагам:
- Возьмите циркуль и поставьте его концом на одну из вершин основания равнобедренного треугольника.
- Расстояние между концом циркуля и вершиной основания должно быть больше половины длины основания.
- Нарисуйте окружность с центром в вершине основания, используя циркуль.
- Опустите перпендикулярную линию из верхней вершины треугольника на основание.
- Точка пересечения основания и перпендикулярной линии будет являться вершиной высоты.
Таким образом, вы сможете построить высоту в равнобедренном треугольнике с помощью циркуля.
Результаты и применение полученной высоты
Высота является одной из основных величин, используемых при работе с треугольниками. Она играет важную роль во многих геометрических и физических задачах, таких как нахождение площади треугольника, определение его центра тяжести, вычисление объема и поверхности, а также решение многих других задач.
Благодаря возможности построения высоты с помощью циркуля, геометрические задачи, связанные с равнобедренными треугольниками, могут быть решены более точно и удобно. Получение точных значений высоты позволяет избежать погрешностей, связанных с округлением и приближенными методами решения.
Кроме того, высота равнобедренного треугольника может быть использована для определения других величин и свойств треугольника, например, углов и длин его сторон. Это позволяет упростить решение сложных геометрических задач и облегчить процесс доказательства геометрических теорем.
Таким образом, построение высоты с помощью циркуля в равнобедренном треугольнике имеет широкий диапазон применений и является необходимым инструментом для геометрических и физических исследований.