Регрессионный анализ – мощный инструмент в области статистики и машинного обучения, который позволяет изучать взаимосвязи между зависимой переменной и одной или несколькими независимыми переменными. Взвешенная модель регрессии является одним из вариантов регрессионного анализа, которая учитывает веса независимых переменных для более точного предсказания зависимой переменной.
Построение взвешенной модели регрессии требует точного понимания основных шагов и методов. В данной статье мы рассмотрим подробный гайд по построению взвешенной модели регрессии, который поможет вам эффективно использовать этот инструмент для своих исследований или бизнес-целей.
В начале процесса необходимо определить цель вашего исследования или анализа. Четко сформулируйте, какая зависимая переменная вам требуется прогнозировать и какие независимые переменные вы собираетесь использовать. Взвешенная модель регрессии может быть особенно полезна в случаях, когда некоторые независимые переменные имеют большее влияние на зависимую переменную, чем другие. Это свойство весов позволяет повысить точность модели и предсказания.
Далее следует собрать данные для анализа. Убедитесь, что все необходимые переменные занесены в таблицу и подготовлены к дальнейшей работе. Взвешенная модель регрессии требует корректной оценки веса каждой независимой переменной. При этом следует установить соответствующую величину веса в зависимости от важности каждой переменной для исследования. Факторы, имеющие меньшее значение, могут иметь меньший вес. Этот процесс требует обоснованности и экспертной оценки.
Принципы построения взвешенной модели регрессии

- Определение важности наблюдений. Взвешенная модель регрессии уделяет больше внимания наиболее значимым наблюдениям, которые могут иметь большой вклад в предсказание регрессионной модели. Веса наблюдений могут быть определены на основе различных факторов, таких как статистическая значимость, количество доступных данных и экспертное мнение.
- Подготовка данных. Перед построением взвешенной модели регрессии необходимо провести предварительную обработку данных и подготовить их для анализа. Это может включать очистку данных от выбросов и пропущенных значений, преобразование переменных, включение взаимодействий между переменными и другие техники.
- Выбор регрессионной модели. Взвешенная модель регрессии может использовать любую известную модель, такую как линейная регрессия, полиномиальная регрессия или другие алгоритмы машинного обучения. Выбор модели основывается на характеристиках данных и поставленной задаче.
- Оценка весов. После определения важности наблюдений можно приступить к оценке весов для каждого наблюдения. Оценка весов может производиться различными методами, например, с помощью статистических тестов или экспертного мнения.
- Построение модели. Построение взвешенной модели регрессии происходит с учетом рассчитанных весов наблюдений. Веса могут быть учтены в формуле модели или при использовании специальных алгоритмов, которые учитывают веса наблюдений.
- Оценка и интерпретация модели. После построения модели необходимо оценить ее качество и интерпретировать полученные результаты. Это может включать оценку значимости коэффициентов модели, анализ статистической значимости модели в целом и проверку ее прогностических способностей.
Взвешенная модель регрессии позволяет учесть разные важности наблюдений и повысить точность предсказания регрессионной модели. Однако, необходимо тщательно определить веса наблюдений и провести оценку и интерпретацию модели с учетом этих весов.
Изучение и подготовка данных для модели

Прежде чем приступить к построению взвешенной модели регрессии, необходимо внимательно изучить и подготовить данные. Качество и точность модели в значительной степени зависят от качества данных, использованных при ее обучении.
Изучение данных включает в себя ознакомление с основными статистическими характеристиками, такими как среднее значение, медиана, стандартное отклонение, минимальное и максимальное значения и прочие. Это позволяет получить представление о распределении данных и выявить возможные выбросы или аномальные значения.
Подготовка данных включает в себя их обработку для удаления или заполнения пропущенных значений, преобразование категориальных переменных в числовые, нормализацию или стандартизацию данных. Также, при необходимости, можно применить методы сэмплирования данных для балансировки выборки или уменьшения ее объема.
Важным шагом подготовки данных является проведение анализа корреляции между признаками. Это позволяет выявить зависимости и взаимосвязи между переменными, а также определить наиболее значимые признаки для модели.
При подготовке данных необходимо также учесть особенности модели и требования алгоритма, которым будет использоваться модель. Например, некоторые алгоритмы требуют нормализации данных, чтобы значения признаков находились в определенном диапазоне.
- Ознакомиться с основными характеристиками данных
- Удалить или заполнить пропущенные значения
- Преобразовать категориальные переменные в числовые
- Нормализовать или стандартизировать данные
- Выявить корреляцию между признаками
- Учесть требования алгоритма, используемого для моделирования
Подготовка данных - важный этап работы с моделью, который позволяет обеспечить ее эффективность и точность предсказаний. Тщательное изучение и обработка данных помогут создать взвешенную модель регрессии, способную достоверно прогнозировать результаты на основе имеющихся данных.
Выбор оптимального функционального вида модели

При построении взвешенной модели регрессии необходимо выбрать оптимальный функциональный вид модели, который достаточно точно аппроксимирует зависимость между независимыми и зависимыми переменными. Выбор функционального вида модели основывается на анализе данных и знании о предметной области.
Один из самых простых и распространенных функциональных видов модели - линейный. Линейная модель предполагает, что зависимая переменная линейно зависит от независимых переменных. Такая модель представляется уравнением вида:
y = β₀ + β₁x₁ + β₂x₂ + ... + βₓxₓ
где y - зависимая переменная, x₁, x₂, ..., xₓ - независимые переменные, β₀, β₁, β₂, ..., βₓ - коэффициенты модели. Данная модель подходит для задач, в которых зависимость между переменными является линейной.
Однако, в некоторых случаях линейная модель может быть недостаточно гибкой для аппроксимации данных. В таких случаях можно рассмотреть использование других функциональных видов модели, таких как:
| Функциональный вид модели | Уравнение модели | Описание |
|---|---|---|
| Полиномиальная | y = β₀ + β₁x + β₂x² + ... + βₙxⁿ | Модель, в которой зависимая переменная аппроксимируется полиномом степени ⁿ |
| Экспоненциальная | y = β₀e^(β₁x) | Модель, в которой зависимая переменная экспоненциально зависит от независимой переменной |
| Логарифмическая | y = β₀ + β₁ln(x) | Модель, в которой зависимая переменная логарифмически зависит от независимой переменной |
| Степенная | y = β₀x^(β₁) | Модель, в которой зависимая переменная степенно зависит от независимой переменной |
Выбор оптимального функционального вида модели требует анализа данных, исследования предметной области и попытки различных вариантов моделей. Некоторые функциональные виды моделей могут иметь физическую интерпретацию, что облегчает понимание зависимостей в данных.
Оценка значимости факторов в модели
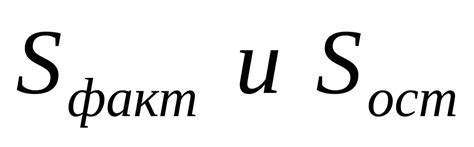
Для оценки значимости факторов в модели могут использоваться различные статистические методы, включая коэффициенты значимости, p-значения и доверительные интервалы.
Один из наиболее распространенных методов - это проверка значимости коэффициентов регрессии. Коэффициент регрессии показывает, насколько изменится зависимая переменная с изменением фактора при всех остальных постоянных переменных. Для каждого фактора в модели вычисляется его коэффициент регрессии, а затем проводится статистическая проверка гипотезы о значимости этого коэффициента. Если полученное p-значение меньше заранее выбранного уровня значимости (обычно 0,05), то фактор считается статистически значимым.
Другим методом оценки значимости факторов является анализ доверительных интервалов. Доверительный интервал показывает диапазон значений, в пределах которого с определенной вероятностью находится истинное значение коэффициента регрессии. Если доверительный интервал для коэффициента не содержит нуля, то это указывает на его значимость.
Также можно использовать и другие методы, например, информационные критерии Акаике (AIC) или Байеса (BIC). Они позволяют сравнить различные модели и выбрать наилучшую с точки зрения баланса между объяснительной способностью и сложностью модели.
| Фактор | Коэффициент регрессии | P-значение | Доверительный интервал |
|---|---|---|---|
| Фактор 1 | 0.356 | 0.015 | [0.130, 0.582] |
| Фактор 2 | 0.213 | 0.102 | [-0.054, 0.480] |
| Фактор 3 | 0.469 | 0.002 | [0.281, 0.657] |
В таблице приведены примеры оценки значимости факторов в модели регрессии. Для каждого фактора указан его коэффициент регрессии, p-значение и доверительный интервал. Из таблицы видно, что фактор 1 и фактор 3 являются статистически значимыми, так как их p-значение меньше выбранного уровня значимости 0,05 и доверительный интервал не содержит нуля. Фактор 2, в свою очередь, не является статистически значимым, так как его p-значение больше 0,05 и доверительный интервал содержит нулевое значение.
Вычисление весов для каждого фактора
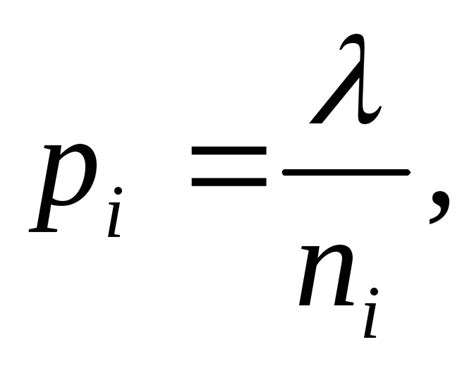
При построении взвешенной модели регрессии необходимо вычислить веса для каждого фактора, чтобы учесть их важность в предсказании зависимой переменной. Вес показывает, насколько велика влияние данного фактора на предсказание.
Вычисление весов происходит с помощью различных методов, например, метода наименьших квадратов или метода максимального правдоподобия. В обоих случаях основная идея заключается в минимизации разницы между предсказанной и наблюдаемой зависимой переменной.
Метод наименьших квадратов (МНК) является наиболее распространенным методом для вычисления весов. Он основан на минимизации суммы квадратов отклонений между наблюдаемыми и предсказанными значениями зависимой переменной.
Метод максимального правдоподобия (ММП) предполагает, что вероятность наблюдаемых данных зависит от параметров модели. Целью ММП является максимизация функции правдоподобия, которая определяет, насколько хорошо модель объясняет наблюдаемые данные.
После определения метода для вычисления весов необходимо применить его к набору данных, чтобы получить значения весов для каждого фактора. Полученные веса можно интерпретировать как меру важности каждого фактора.
Веса могут быть положительными или отрицательными, в зависимости от направления влияния фактора на зависимую переменную. Чем больше абсолютное значение веса, тем сильнее влияние фактора на предсказание.
Вычисление весов для каждого фактора является важным шагом при построении взвешенной модели регрессии. Он позволяет учесть различную важность факторов и получить более точные предсказания зависимой переменной.
Учет весов при построении модели

При построении взвешенной модели регрессии важно учесть веса каждого наблюдения, чтобы корректно оценить влияние каждого предиктора на целевую переменную.
Веса могут быть разными в зависимости от значимости наблюдений или от их размера. Часто веса вычисляются с использованием метода наименьших квадратов (OLS). Веса, вычисленные с помощью OLS, учитывают влияние ошибок в модели и помогают сделать оценки более точными.
Процесс построения взвешенной модели регрессии включает следующие шаги:
- Вычисление весов для каждого наблюдения с использованием метода OLS.
- Взвешенное обучение модели, применяя веса к каждому наблюдению.
- Оценка значимости предикторов с использованием взвешенной модели.
При построении взвешенной модели регрессии особое внимание следует уделять правильному выбору весов. Выбор неоптимальных весов может привести к неправильным оценкам и недостоверным результатам. Поэтому рекомендуется применять методы, которые позволяют определить наилучшие веса для каждого наблюдения.
Оценка качества модели
1. Средняя абсолютная ошибка (Mean Absolute Error, MAE)
MAE измеряет среднее абсолютное отклонение между прогнозируемыми значениями модели и фактическими значениями целевой переменной. Чем меньше значение MAE, тем лучше модель. Данную метрику можно вычислить с помощью следующей формулы:
где n - общее количество наблюдений, yi - фактическое значение целевой переменной, ŷi - прогнозируемое значение целевой переменной.
2. Среднеквадратическая ошибка (Mean Squared Error, MSE)
MSE измеряет среднее квадратичное отклонение между прогнозируемыми значениями модели и фактическими значениями целевой переменной. Чем меньше значение MSE, тем лучше модель. Данную метрику можно вычислить с помощью следующей формулы:
где n - общее количество наблюдений, yi - фактическое значение целевой переменной, ŷi - прогнозируемое значение целевой переменной.
3. Коэффициент детерминации (R-квадрат, R^2)
R-квадрат показывает, насколько хорошо модель объясняет изменчивость целевой переменной. Значение R^2 находится в диапазоне от 0 до 1, где 1 означает идеальное соответствие модели и фактических значений. Данную метрику можно вычислить с помощью следующей формулы:
где yi - фактическое значение целевой переменной, ŷi - прогнозируемое значение целевой переменной, ȳ - среднее значение целевой переменной.
Для более точной оценки качества модели рекомендуется использовать несколько метрик вместе. Также стоит учитывать предметную область и особенности задачи, чтобы выбрать наиболее подходящие метрики для конкретной модели.
| Метрика | Описание | Преимущества | Недостатки |
|---|---|---|---|
| MAE | Измеряет среднее абсолютное отклонение | Робастная к выбросам | Не учитывает величину отклонения |
| MSE | Измеряет среднее квадратичное отклонение | Учитывает величину отклонения | Чувствительна к выбросам |
| R^2 | Показывает соответствие модели и фактических значений | Интерпретируемая метрика | Не учитывает ошибки предсказаний |
Тестирование модели на новых данных
После построения взвешенной модели регрессии следует провести тестирование на новых данных. Это необходимо для оценки точности модели и проверки ее способности предсказывать значения зависимой переменной.
Тестирование модели на новых данных можно провести следующим образом:
- Разделите имеющиеся данные на обучающую и тестовую выборки. Обычно используют соотношение 70%:30% или 80%:20%. Обучающая выборка используется для обучения модели, а тестовая выборка - для проверки ее качества.
- Запустите модель на обучающей выборке. Модель будет обучаться на данных и настраивать свои веса.
- Получите предсказания модели на тестовой выборке. То есть, модель будет использоваться для предсказания значений зависимой переменной на основе входных данных из тестовой выборки.
- Сравните предсказанные значения с фактическими значениями зависимой переменной из тестовой выборки. Для оценки точности модели можно использовать различные метрики, например, среднеквадратичную ошибку (MSE) или коэффициент детерминации (R-squared).
Важно отметить, что результаты тестирования на новых данных могут отличаться от результатов, полученных на обучающей выборке. Поэтому рекомендуется проводить кросс-валидацию и усреднять показатели точности модели на разных подмножествах данных.
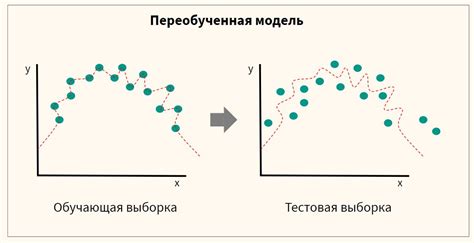
Если модель демонстрирует хорошую точность на тестовой выборке, это говорит о ее способности обобщать и предсказывать значения зависимой переменной на новых данных. Если же модель показывает низкую точность на тестовой выборке, это может свидетельствовать о переобучении модели на обучающей выборке или о недостаточной обобщающей способности модели.
Регуляризация и улучшение модели
Существует два типа регуляризации: L1-регуляризация и L2-регуляризация.
При использовании L1-регуляризации, также известной как лассо-регуляризация, некоторые коэффициенты весов признаков могут быть уменьшены до нуля. Это позволяет выбрать наиболее значимые признаки и уменьшить количество признаков в модели. Таким образом, лассо-регуляризация работает как метод отбора признаков.
При использовании L2-регуляризации, также известной как гребневая регрессия, коэффициенты весов признаков могут быть уменьшены, но не до нуля. Это позволяет уменьшить влияние "шумовых" признаков и повысить стабильность модели. Гребневая регрессия работает как метод сжатия весов признаков.
Выбор между L1-регуляризацией и L2-регуляризацией зависит от конкретной задачи и данных. Если требуется уменьшить количество признаков и выбрать наиболее значимые, лассо-регуляризация может быть предпочтительной. Если же важнее повысить стабильность модели и уменьшить влияние "шумовых" признаков, гребневая регрессия может быть более подходящей.
| Метод регуляризации | Преимущества | Недостатки |
|---|---|---|
| L1-регуляризация | - Отбор наиболее значимых признаков - Уменьшение сложности модели | - Может уменьшить количество признаков до 0 - Может быть менее стабильной |
| L2-регуляризация | - Уменьшение влияния "шумовых" признаков - Повышение стабильности модели | - Не отбирает признаки до 0 - Может сохранять "шумовые" признаки |
Регуляризация является важным инструментом для улучшения моделей регрессии. Она может помочь контролировать значимость признаков, уменьшить переобучение и улучшить обобщающую способность модели.