Когда речь заходит о визуализации статистических данных, ящик с усами - это один из самых мощных инструментов, который позволяет наглядно представить распределение значений и ключевые метрики.
Ящик с усами состоит из медианы, вертикальной центральной линии, отметки для первого и третьего квартилей, а также усов, которые являются пределами распределения.
Этот инструмент особенно полезен при анализе данных в области экономики, финансов, медицины и маркетинга. В данной статье мы рассмотрим, как построить ящик с усами в статистике и как использовать его для анализа данных. Мы также предоставим наглядные примеры, чтобы вы могли лучше понять, как применять эту визуализацию в своих исследованиях.
Что такое ящик с усами в статистике?

График представляет собой прямоугольник, который называется ящик. Верхняя и нижняя границы ящика соответствуют третьему квартилю (Q3) и первому квартилю (Q1) соответственно. Внутри ящика находится середина значений, которую называют медианой.
Кроме того, на графике есть две отдельные линии, выходящие из ящика, которые называются усами. Верхний ус отображает предельное значение данных, не считая выбросы, а нижний ус указывает на минимальное значение в наборе данных.
Ящик с усами дополняется точками или другими символами, которые называются выбросами. Выбросы показывают значения, которые значительно отличаются от основного распределения данных.
Этот тип графика позволяет быстро и наглядно оценить основные статистические характеристики набора данных, идентифицировать наличие выбросов и сравнивать распределение данных между группами или категориями.
Основные характеристики ящика с усами
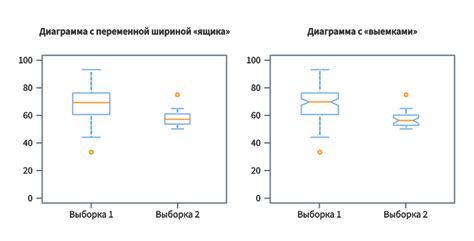
Главные характеристики ящика с усами включают:
| Медиана | - среднее значение данных, разделенное так, что 50% значений находятся ниже, а остальные 50% - выше. |
| Нижний квартиль (Q1) | - значение, ниже которого находится 25% данных. |
| Верхний квартиль (Q3) | - значение, ниже которого находится 75% данных. |
| Минимальное значение | - наименьшее значение в наборе данных, не считая выбросы. |
| Максимальное значение | - наибольшее значение в наборе данных, не считая выбросы. |
| Выбросы | - значения, находящиеся далеко от основного распределения и считающиеся необычными или аномальными. |
Ящик с усами может быть полезным инструментом для визуализации и анализа распределения данных, позволяя быстро и наглядно оценить их основные характеристики.
Преимущества использования ящика с усами

- Позволяет быстро визуализировать основные характеристики набора данных, такие как медиана, интерквартильный размах, выбросы и асимметрия.
- Помогает исследователям быстро сравнивать несколько групп или условий и определять наличие значимых различий.
- Облегчает выявление выбросов или аномальных значений, которые могут искажать общую картину данных.
- Удобен в использовании и понятен даже для тех, кто не разбирается в статистике, благодаря простому и интуитивному представлению данных.
- Позволяет проводить сравнительный анализ данных и отображать результаты на одной диаграмме, что удобно для сопоставления различных групп или условий.
Принцип построения ящика с усами
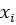
Процесс построения ящика с усами начинается с расчета статистических показателей. Сначала необходимо определить медиану, которая является значением, разделяющим упорядоченный набор данных на две равные части. Затем вычисляются первый и третий квартили, которые представляют собой значения, разделяющие оставшиеся значения на четыре равные части.
Для построения ящика с усами необходимо определить диапазон значений, включающий минимальное и максимальное значение в наборе данных. Верхняя граница ящика устанавливается на третьем квартиле, а нижняя граница - на первом квартиле. Внутри ящика, на уровне медианы, рисуется горизонтальная линия.
Можно увидеть, что границы ящика и усы проходят не по фактическим значениям, а по уровню, который зависит от размаха, размера выборки и выбранного коэффициента.
Усы ящика представляют собой "усики", которые охватывают значения внутри диапазона, не считая выбросы. Верхний ус достигает максимального значения, не считая выбросов, а нижний ус - минимального значения.
Выбор категорий и переменных для построения

Выбор категорий основан на природе данных и цели исследования. Категории могут быть представлены категориями товаров, возрастными группами, географическими регионами и другими параметрами, которые характеризуют выборку данных. Важно выбрать категории таким образом, чтобы они были релевантными и информативными для анализа.
При выборе переменных необходимо оценить их влияние на исследуемый параметр. Важно выбрать те переменные, которые имеют значительную связь с анализируемыми данными и могут внести ценный вклад в исследование. Величины, которые не оказывают значимого влияния на исследуемую переменную, могут быть исключены из выборки для более точного отображения данных.
При выборе категорий и переменных также необходимо принять во внимание доступность данных. Если данные по определенным категориям или переменным отсутствуют или их количество недостаточно для анализа, это может затруднить построение и интерпретацию ящика с усами.
Важно сделать выбор категорий и переменных внимательно и основательно, чтобы гарантировать правильность и достоверность полученных результатов построения ящика с усами в статистике.
Вычисление квартилей для определения границ ящика

Для вычисления границы ящика с усами необходимо определить первый (нижний) и третий (верхний) квартили. Первый квартиль (Q1) представляет собой значение, которое разделяет нижние 25% данных от верхних 75%. Третий квартиль (Q3) разделяет нижние 75% данных от верхних 25%.
Чтобы вычислить квартили, необходимо упорядочить данные в возрастающем порядке. Затем находятся индексы элементов, которые соответствуют первому и третьему квартилям. Если количество данных нечетное, то индексы вычисляются по формулам:
Q1 = (n + 1) / 4
Q3 = (3 * (n + 1)) / 4
Если же количество данных четное, то индексы равны:
Q1 = n / 4
Q3 = 3 * (n / 4)
Где n – количество данных.
После вычисления индексов находятся соответствующие значения данных и используются в диаграмме ящика с усами для определения нижней и верхней границ ящика.
Вычисление границ усов
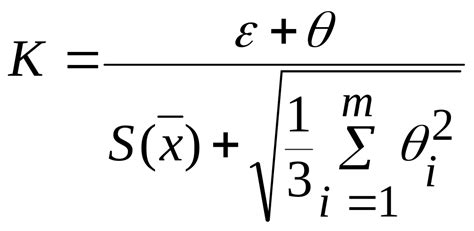
Для построения ящика с усами в статистике необходимо вычислить границы усов. Границы усов определяются на основе статистических метрик, таких как квартили, медиана и выбросы.
Процесс вычисления границ усов можно выполнить следующим образом:
- Вычислить первый квартиль (нижний квартиль). Это значение разделяет нижнюю половину данных от верхней половины данных.
- Вычислить третий квартиль (верхний квартиль). Это значение разделяет верхнюю половину данных от нижней половины данных.
- Вычислить межквартильный размах - разницу между третьим и первым квартилями. Это значение показывает степень разброса данных.
- Если в данных присутствуют выбросы, определить их и исключить из расчетов.
- Вычислить нижнюю границу усов как третий квартиль минус 1,5 межквартильных размахов.
- Вычислить верхнюю границу усов как третий квартиль плюс 1,5 межквартильных размахов.
После вычисления границ усов можно построить ящик с усами, где медиана будет представлена линией внутри ящика, верхняя и нижняя границы ящика обозначают первый и третий квартили соответственно, а усы – это линии, которые простираются от границ ящика до минимального и максимального значения, не считая выбросы.
Вычисление границ усов является важным шагом при построении ящика с усами, так как позволяет визуализировать основные метрики данных и обнаружить наличие выбросов.
Пример вычисления границ усов:
| Данные | Первый квартиль | Третий квартиль | Межквартильный размах | Нижняя граница усов | Верхняя граница усов |
|---|---|---|---|---|---|
| 10, 15, 20, 25, 30, 35, 40, 45, 50 | 15 | 40 | 25 | -17.5 | 72.5 |
В данном примере первый квартиль равен 15, третий квартиль равен 40, межквартильный размах равен 25, нижняя граница усов равна -17.5, а верхняя граница усов равна 72.5. Наличие выбросов можно определить, сравнив значение минимального и максимального значения с границами усов.
Примеры использования ящика с усами в статистике
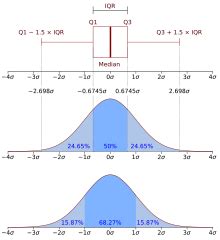
Ниже приведены несколько примеров использования ящика с усами в статистике:
Исследование оценок студентов: Представление оценок студентов по предмету в виде ящика с усами может помочь исследователям визуализировать диапазон оценок, медиану и выбросы. Это также может помочь выявить различия в успеваемости между группами студентов.
Анализ данных продаж: Построение ящика с усами для продаж может помочь исследователям оценить степень изменчивости продаж и выявить выбросы. Это может быть полезно для идентификации тенденций в продажах и понимания различий между регионами или продуктами.
Сравнение распределений: С помощью ящика с усами можно сравнить распределения нескольких наборов данных и определить, есть ли статистически значимые различия между ними. Например, можно сравнить распределения доходов мужчин и женщин или оценить эффективность различных лекарственных препаратов.
Это лишь некоторые примеры того, как ящик с усами может быть использован в статистике. Важно помнить, что он является всего лишь одним из инструментов анализа данных и не должен рассматриваться в отрыве от других методов и техник статистического анализа.
Анализ распределения доходов разных групп населения
Для проведения анализа распределения доходов различных групп населения мы используем метод построения ящика с усами. Этот метод включает в себя графическую визуализацию данных, позволяющую легко сравнивать и анализировать различия в распределении доходов между группами.
Для начала, мы собираем данные о доходах разных групп населения. Каждая группа представляет собой набор значений доходов, которые затем используются для построения ящика с усами.
Ящик с усами представляет собой прямоугольник, где его вертикальная линия разделяет ящик на две части. Вертикальная линия обозначает медиану - значение, разделяющее набор данных пополам. Внутри ящика также отображается интерквартильный размах - разница между первым и третьим квартилями. Это дает нам представление о разбросе данных внутри ящика.
Для лучшего понимания распределения данных, мы также добавляем усы к ящику. Верхний ус представляет собой линию, которая простирается выше ящика и отражает максимальное значение данных (исключая выбросы). Нижний ус представляет собой линию, простирающуюся ниже ящика и отражает минимальное значение данных (исключая выбросы).
Анализируя ящик с усами для разных групп населения, мы можем сравнивать их распределение доходов. Если ящики разных групп перекрываются, это указывает на схожее распределение данных. Если же ящики не перекрываются, это может указывать на значительные различия в распределении между группами.
| Группа населения | Медиана | Первый квартиль | Третий квартиль | Минимальное значение | Максимальное значение |
|---|---|---|---|---|---|
| Группа A | 20 000 | 15 000 | 25 000 | 10 000 | 30 000 |
| Группа B | 25 000 | 20 000 | 30 000 | 15 000 | 40 000 |
| Группа C | 15 000 | 10 000 | 20 000 | 5 000 | 25 000 |
В приведенной таблице представлены данные о доходах трех групп населения - A, B и C. Мы видим, что медиана доходов в группах A, B и C составляет соответственно 20 000, 25 000 и 15 000. Первый квартиль группы A равен 15 000, группы B - 20 000 и группы C - 10 000. Третий квартиль группы A равен 25 000, группы B - 30 000 и группы C - 20 000. Минимальное значение дохода в группе A составляет 10 000, в группе B - 15 000 и группе C - 5 000. Максимальное значение дохода в группе A составляет 30 000, в группе B - 40 000 и группе C - 25 000.
Сравнение продолжительности сна у разных возрастных групп
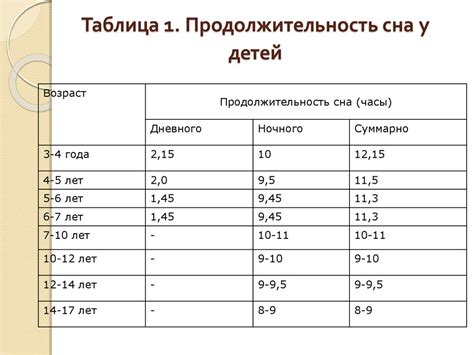
Исследование продолжительности сна у различных возрастных групп имеет большое значение для понимания влияния сна на здоровье и благополучие людей. В данном разделе мы рассмотрим результаты такого сравнительного анализа для нескольких возрастных групп.
1. Дети дошкольного возраста (3-5 лет):
- Средняя продолжительность сна: 11-13 часов
- Рекомендуемая продолжительность сна: около 12 часов
- Наиболее общие проблемы со сном: бессонница, ночные кошмары
2. Дети школьного возраста (6-12 лет):
- Средняя продолжительность сна: 9-11 часов
- Рекомендуемая продолжительность сна: 10-11 часов
- Наиболее общие проблемы со сном: отсутствие регулярного режима сна, сонливость днем
3. Подростки (13-18 лет):
- Средняя продолжительность сна: 8-10 часов
- Рекомендуемая продолжительность сна: 8-9 часов
- Наиболее общие проблемы со сном: отсутствие регулярного режима сна, сонливость днем
4. Взрослые (18-64 года):
- Средняя продолжительность сна: 7-9 часов
- Рекомендуемая продолжительность сна: 7-9 часов
- Наиболее общие проблемы со сном: бессонница, сонливость днем
5. Пожилые люди (65+ лет):
- Средняя продолжительность сна: 7-8 часов
- Рекомендуемая продолжительность сна: 7-8 часов
- Наиболее общие проблемы со сном: пробуждение ночью, частые перерывы во сне
Эти данные позволяют сравнить рекомендуемую продолжительность сна для разных возрастных групп с их фактической продолжительностью сна. Исходя из этого сравнения, можно оценить, насколько сон соответствует нормам и определить возможные проблемы со сном, указывающие на необходимость коррекции режима сна. Учитывая значение сна для общего физического и психического здоровья, необходимо стремиться к достижению оптимальной продолжительности и качества сна в каждой возрастной группе.