Корень числа является одним из основных математических понятий, с которым мы сталкиваемся ежедневно. Знание методов вычисления корня числа может быть полезным для решения различных задач - от простых арифметических операций до более сложных математических и инженерных проблем. Этот материал даст вам ясное представление о различных способах нахождения корня числа и поможет вам справиться с этой задачей легко и эффективно.

При вычислении корня числа важно иметь представление о том, что есть разные методы для разных типов чисел и ситуаций. В статье мы рассмотрим методы для целых чисел, десятичных дробей и комплексных чисел. Основной метод вычисления корня числа - это итерационный процесс, который позволяет приближенно находить решение с заданной точностью. Узнайте, как правильно применять различные формулы и алгоритмы для разных случаев, и вы сможете с легкостью вычислять корень числа в разных ситуациях.

Кроме основных методов вычисления корня числа, в статье мы также рассмотрим некоторые полезные советы, которые помогут вам работать эффективнее. Вы узнаете о том, как выбрать наиболее подходящий метод для конкретной задачи, как улучшить точность вычислений и как обращаться с возможными ошибками. Мы представим ясные примеры и пошаговые инструкции, которые помогут вам овладеть этими методами с минимальными усилиями.

Практические методы вычисления корня числа

Один из самых простых и широко используемых методов - это метод нахождения квадратного корня с помощью итераций. Для этого необходимо выбрать начальное приближение и последовательно уточнять его, используя следующую формулу:

X_n+1 = (X_n + (A / X_n)) / 2

Где X_n - текущее приближение, A - число, для которого вычисляется корень. Чем больше итераций будет выполнено, тем точнее будет получен результат.

Еще один метод вычисления корня числа - это метод бинарного поиска. Для этого необходимо определить верхнюю и нижнюю границу, так чтобы значение числа находилось между ними. Затем, на каждой итерации, проверять, находится ли середина интервала ближе к корню или к исходному числу, и соответствующим образом обновлять границы. По мере увеличения числа итераций получаем все более точное значение корня.

Однако, стоит отметить, что методы вычисления корня числа являются итеративными и всегда дают приближенный результат. Для получения более точного значения необходимо увеличивать число итераций или применять более сложные алгоритмы.

Важным аспектом при использовании методов вычисления корня числа является выбор начального приближения. Чем ближе это значение к искомому корню, тем быстрее и точнее будет получен результат. Поэтому, при выборе начального значения следует учитывать характеристики задачи и предполагаемое значение корня.

Простые алгоритмы и приемы

Алгоритм деления пополам. Этот метод основан на простой итерации. Суть его заключается в том, что начальное число, корень которого нужно вычислить, разбивается на две части. Затем происходит итерационный процесс, где проверяется, в какой половине находится корень. Таким образом, каждый раз число сокращается в два раза, пока не будет достигнута нужная точность. Это простой и эффективный способ вычисления корня числа.

Пример: Для вычисления корня числа 64 мы начинаем с диапазона от 0 до 64. Затем выбираем середину этого диапазона (32). Если квадрат середины больше искомого числа, то диапазон сдвигается влево, иначе – вправо. Повторяем этот процесс до тех пор, пока не достигнем нужной точности. В итоге получим корень числа 64, равный 8.

Итерационный метод Ньютона. Этот метод основан на итерации и применяется для вычисления корня уравнения. Он работает путем нахождения касательной к кривой графика функции и нахождения ее корня. Затем процесс повторяется, пока не достигнется нужная точность. Этот метод является одним из самых точных алгоритмов вычисления корня числа.

Пример: Если нам нужно найти корень числа 36, то мы начинаем с начального приближения (например, 6). Затем используем формулу x = (x + n / x) / 2 для нахождения следующего приближения. Повторяем этот процесс до достижения нужной точности. В конечном итоге получим корень числа 36, равный 6.

Метод Ньютона-Рафсона и его применение

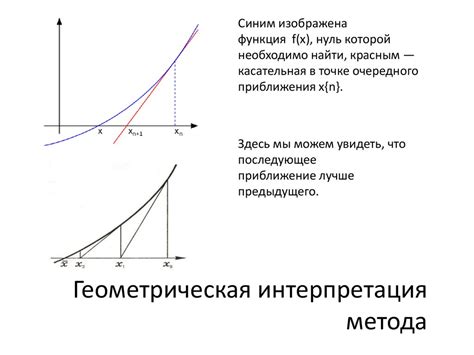
Для применения этого метода необходимо знать значение функции и ее производной в точке, близкой к искомому корню. Начальное приближение можно получить, используя другие методы, например, метод деления отрезка пополам.

• Шаг 1: Задать начальное приближение x₀.
• Шаг 2: Вычислить значение функции f(x₀) и ее производной f'(x₀).
• Шаг 3: Вычислить приближение корня x₁ с помощью формулы x₁ = x₀ - f(x₀)/f'(x₀).
• Шаги 2 и 3 повторяются, пока значение f(x) не станет достаточно близким к нулю.

Метод Ньютона-Рафсона является итеративным методом, то есть он требует нескольких итераций для нахождения корня с заданной точностью. Чем ближе начальное приближение к искомому корню, тем быстрее сходится алгоритм.

Этот метод широко используется в различных областях, таких как физика, финансы, инженерия и т.д. Он позволяет находить корни сложных функций и решать нелинейные уравнения. Благодаря своей эффективности и точности, метод Ньютона-Рафсона является незаменимым инструментом для численного анализа.

Аналитическое решение для некоторых случаев

Хотя числа можно вычислить численными методами, существуют некоторые случаи, в которых корень можно выразить аналитически. Некоторые из таких случаев включают:

• Квадратные числа: если число является квадратом некоторого целого числа, то корень может быть выражен точно и равен этому целому числу.
• Рациональные числа: если число является рациональным числом, то его корень можно выразить аналитически в виде дроби.
• Некоторые специальные числа: существуют несколько известных особых чисел, у которых корень может быть выражен аналитически, например, число Пи (π) или Неперово число (e).

В этих случаях аналитическое решение позволяет найти точное значение корня без необходимости прибегать к численным методам.

Использование библиотек и программных инструментов

Вычисление корня числа может быть упрощено с использованием различных библиотек и программных инструментов. Ниже представлены несколько популярных инструментов, которые можно использовать для этой задачи.

• Библиотека math.h в языке C: Эта библиотека содержит функцию sqrt(), которая позволяет вычислить корень числа в языке C. Просто подключите библиотеку math.h и используйте функцию sqrt() для вычисления корня числа.
• Библиотека math в языке Python: В языке Python есть встроенная библиотека math, которая предоставляет функцию sqrt(). Вызовите функцию sqrt() и передайте ей число в качестве аргумента, чтобы вычислить корень этого числа.
• Программа Microsoft Excel: Если вы предпочитаете использовать графический интерфейс, то программа Microsoft Excel может быть очень полезной. Вы можете использовать функцию SQRT() в Excel, чтобы вычислить корень числа. Просто введите формулу в ячейку и Excel автоматически выполнит вычисление.
• Онлайн-калькуляторы: В Интернете есть множество онлайн-калькуляторов, которые позволяют вычислять корень числа. Просто найдите один из таких калькуляторов и введите число, для которого нужно вычислить корень. Калькулятор выполнит вычисление и выдаст результат.

Использование библиотек и программных инструментов упрощает вычисление корня числа и позволяет сэкономить время и усилия. Выберите тот инструмент, который наиболее удобен для вас, и наслаждайтесь удобством работы с числами!