Деление десятичных дробей является одной из ключевых тем в математике, которую учат в школе и высшем образовании. Эта операция может показаться сложной на первый взгляд, но с правильным пониманием правил и достаточной практикой она становится достаточно простой и легко выполняется. В этом руководстве мы разберем основные правила деления десятичных дробей и рассмотрим примеры, чтобы помочь вам разобраться в этой теме.
Перед тем как начать деление десятичных дробей, важно понять, что десятичная дробь может быть представлена в виде обыкновенной дроби, где числитель - это десятичное число без запятой, а знаменатель - определенное количество десятков или сотых. Например, число 0.25 может быть записано как 25/100 или 1/4. Это позволяет нам выполнять деление десятичных дробей так же, как и обыкновенных дробей, используя известные правила.
Основное правило для деления десятичных дробей заключается в том, что нужно помножить делимое на обратную величину делителя. Для этого обратим делитель, то есть заменим числитель и знаменатель местами, и затем умножим делимое на получившуюся обратную дробь. В результате получится произведение двух десятичных дробей, которое можно привести к обыкновенной дроби или округлить до заданного количества знаков после запятой.
Определение десятичной дроби и ее деление

Примеры десятичных дробей:
- 0.5 - пять десятых;
- 2.75 - два целых и семьдесят пять сотых;
- 0.123456789 - сто двадцать три миллионных четыреста пятьдесят шесть миллионных семьсот восемьдесят девять миллионных.
Десятичные дроби можно делить друг на друга при помощи особых правил. Деление десятичных дробей требует выполнения ряда шагов.
Шаги деления десятичных дробей:
- Убедитесь, что делитель больше 0.
- Приведите делимое и делитель к одному знаменателю, если они имеют разные знаменатели.
- Разделите целые части делимого и делителя.
- Разделите десятичные части делимого и делителя.
- Выполните обратную операцию и перемножьте частное на делитель.
Понимание правил и умение правильно производить деление десятичных дробей позволит вам решать задачи, связанные с вычислительными операциями и анализом данных.
Правила деления десятичных дробей без остатка
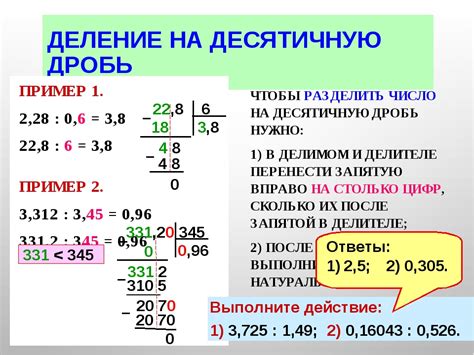
Шаг 1: Начните с записи десятичных дробей, которые вы хотите разделить. Обычно числитель (верхняя часть дроби) записывается над чертой, а знаменатель (нижняя часть дроби) записывается под чертой.
Шаг 2: Переведите десятичные дроби в десятичные числа, переместив запятую влево на несколько разрядов. Например, если у вас есть десятичная дробь 0,25, вы можете перевести ее в десятичное число 0.25.
Шаг 3: Запишите деление, как если бы вы делали деление обычных десятичных чисел. Разделите десятичное число, полученное из числителя, на десятичное число, полученное из знаменателя.
Шаг 4: Если при делении нет остатка, вы получаете ответ без остатка. В этом случае, запишите результат деления справа от десятичной запятой. Например, если вы делите 0.25 на 0.05 и не получаете остатка, то ответ будет 5.
Шаг 5: Проверьте свой ответ, перемножив полученный результат на делитель. Ответ должен равняться числителю исходной десятичной дроби.
Следуя этим правилам, вы сможете легко делить десятичные дроби без остатка и быстро решать задачи, связанные с десятичными дробями.
Правила деления десятичных дробей с остатком

Деление десятичных дробей нередко вызывает затруднения у многих учеников и студентов. Когда в результате деления десятичная дробь не делится нацело, возникает остаток. В этом случае применяются специальные правила для определения и представления остатка. Следует помнить, что при делении десятичных дробей все числа должны быть выровнены по запятой.
Правила деления десятичных дробей с остатком:
- Производим деление десятичной дроби, как обычно.
- Если в результате деления десятичная дробь не делится нацело, остаток записывается после символа "ост.".
- Остаток представляется в виде десятичной дроби, записывая его над делителем, таким образом, что десятичная запятая в остатке выстраивается над той же цифрой в делителе.
- Над остатком ставится ведущий ноль, если после цифр остатка отсутствует какая-либо цифра в делителе.
Пример:
- Делимое: 3.2
- Делитель: 0.5
- 3.2 ÷ 0.5 = 6.4
- Остаток: 0.2
- Ответ: 6.4 (ост. 0.2)
Следуя этим правилам, можно верно выполнять деление десятичных дробей и корректно представлять результат вместе с остатком.
Примеры задач по делению десятичных дробей

Деление десятичных дробей может быть иногда сложным для понимания процессом, но с помощью примеров задач можно легко освоить эту тему.
Пример 1:
Выполните деление:
0.7 ÷ 0.1 = ?
Решение:
Для начала, переведем оба числа в дроби с равными знаменателями:
0.7 ÷ 0.1 = 7/10 ÷ 1/10
Затем, умножим делимое на обратное значение делителя:
7/10 ÷ 1/10 = 7/10 × 10/1 = 70/10 = 7
Ответ: 0.7 ÷ 0.1 = 7
Пример 2:
Выполните деление:
3.6 ÷ 0.2 = ?
Решение:
Переведем оба числа в дроби:
3.6 ÷ 0.2 = 36/10 ÷ 2/10
Далее, умножим делимое на обратное значение делителя:
36/10 ÷ 2/10 = 36/10 × 10/2 = 360/20 = 18
Ответ: 3.6 ÷ 0.2 = 18
Пример 3:
Выполните деление:
2.1 ÷ 0.7 = ?
Решение:
Переведем оба числа в дроби:
2.1 ÷ 0.7 = 21/10 ÷ 7/10
Затем, умножим делимое на обратное значение делителя:
21/10 ÷ 7/10 = 21/10 × 10/7 = 210/70 = 3
Ответ: 2.1 ÷ 0.7 = 3
Пример 4:
Выполните деление:
7.5 ÷ 1.5 = ?
Решение:
Переведем оба числа в дроби:
7.5 ÷ 1.5 = 75/10 ÷ 15/10
Далее, умножим делимое на обратное значение делителя:
75/10 ÷ 15/10 = 75/10 × 10/15 = 750/150 = 5
Ответ: 7.5 ÷ 1.5 = 5
Простейшие примеры деления десятичных дробей помогут вам понять этот процесс и применять его в других задачах. Занимайтесь практикой, и вы станете мастером в делении десятичных дробей!