В линейной алгебре векторы играют ключевую роль и широко используются в различных областях науки и техники. Важной характеристикой векторов является их ортогональность, которая определяется посредством специальных правил и методов.

Ортогональные векторы – это векторы, которые образуют прямой угол между собой. Это значит, что векторы перпендикулярны друг другу. Ортогональность может быть определена с помощью нескольких методов, в том числе геометрических и алгебраических.

Геометрический метод заключается в проверке, образуют ли векторы прямой угол. Для этого необходимо построить векторы на плоскости или в пространстве и проверить, параллельны ли они или пересекаются. Если два вектора пересекаются при прямом угле, то они ортогональны.

Алгебраический метод определения ортогональности векторов основывается на использовании скалярного произведения. Два вектора ортогональны, если их скалярное произведение равно нулю. Это означает, что сумма произведений соответствующих координат векторов равна нулю. Если результат этой операции равен нулю, то векторы являются ортогональными.

Определение ортогональности векторов

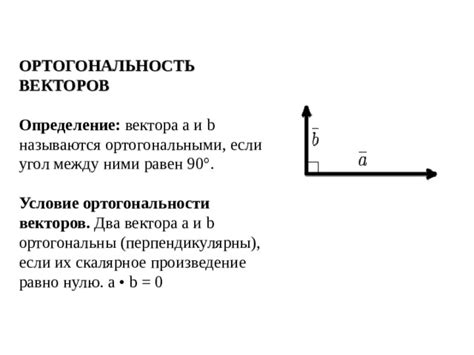
Скалярное произведение двух векторов вычисляется путем умножения соответствующих координат и их суммирования. Если результат равен нулю, это означает, что угол между векторами равен 90 градусам, то есть они перпендикулярны друг другу.

Ортогональные векторы являются важным понятием в линейной алгебре, так как они образуют базис в ортогональном пространстве. Также ортогональность векторов используется в различных приложениях, например, в физике, где она помогает определить направление и распределение сил.

Ортогональность как перпендикулярность векторов

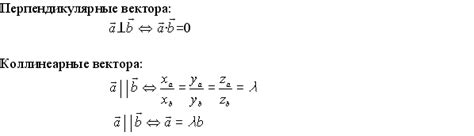
Перпендикулярность векторов означает, что они образуют прямой угол между собой. Другими словами, векторы ортогональны, если их скалярное произведение равно нулю.

Скалярное произведение двух векторов может быть вычислено путем умножения соответствующих компонент векторов и сложения полученных произведений. Если результат равен нулю, то векторы ортогональны.

Ортогональные векторы имеют ряд важных свойств и применений. Например, векторы могут быть использованы для описания физических величин, таких как сила и скорость, и ортогональность позволяет определить независимые компоненты этих величин.

Ортогональность также является важным понятием в геометрии, где она используется для определения пересечения линий и плоскостей.

Ортогональные векторы могут быть визуализированы в трехмерном пространстве как пересекающиеся линии или как перпендикулярные плоскости.

Ортогональность векторов играет ключевую роль в различных областях науки и техники, и понимание этого понятия является важным для решения широкого круга задач и проблем.

Ортогональность векторов посредством скалярного произведения

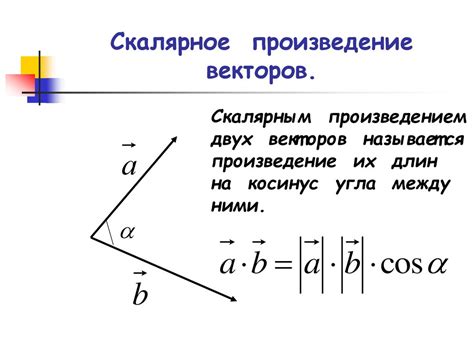
Скалярное произведение двух векторов определяется как произведение их длин и косинуса угла между ними. Если скалярное произведение равно нулю, то векторы считаются ортогональными.

Формула для вычисления скалярного произведения:

scalar_product = a₁ * b₁ + a₂ * b₂ + ... + a_n * b_n,

где a и b - координаты векторов.

При использовании данного метода векторы можно проверять на ортогональность путем вычисления их скалярного произведения и проверки его значения. Если скалярное произведение равно нулю, то векторы ортогональны друг другу.

Методы определения ортогональности векторов

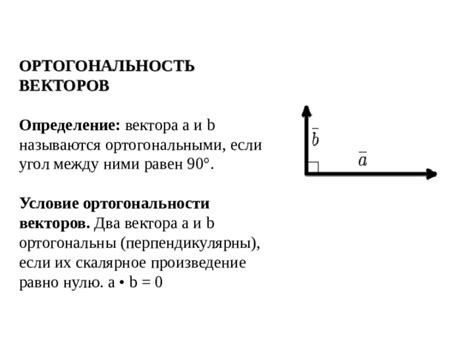
Существует несколько методов определения ортогональности векторов:

1. Метод скалярного произведения. Векторы a и b ортогональны, если их скалярное произведение равно нулю: a · b = 0.
2. Геометрический метод. Векторы a и b ортогональны, если их направления перпендикулярны их длины: