Тригонометрия это раздел математики, который изучает связь между углами и сторонами треугольников. Функции тригонометрии определяются на основе отношений между углами и сторонами треугольников.
В тригонометрии есть шесть основных тригонометрических функций: синус (sin), косинус (cos), тангенс (tan), котангенс (cot), секанс (sec) и косеканс (cosec). Каждая из этих функций определена для угла, выраженного в радианах.
Область определения функций тригонометрии зависит от типа функции. Например, область определения функции синуса (sin) и косинуса (cos) включает все реальные числа. Функции тангенс (tan) и котангенс (cot) определены на всех значениях, кроме тех, где косинус равен нулю. Функции секанс (sec) и косеканс (cosec) определены на всех значениях, кроме тех, где синус равен нулю.
Примеры определения области функций тригонометрии:
- Область определения функции sin(x) и cos(x) - все реальные числа: x ∈ ℝ
- Область определения функции tan(x) и cot(x) - все числа, кроме тех, где cos(x) = 0: x ∈ ℝ, x ≠ (2n + 1)π/2, где n ∈ ℤ
- Область определения функции sec(x) и cosec(x) - все числа, кроме тех, где sin(x) = 0: x ∈ ℝ, x ≠ nπ, где n ∈ ℤ
Знание области определения тригонометрических функций является важным для понимания и применения этих функций в математике и науке в целом.
Основные понятия и определения

Углы, которые мы обычно изучаем в тригонометрии, измеряются в градусах (°) или радианах (rad). В градусной системе угол полного оборота равен 360°, а в радианной системе - 2π радиан.
Главные функции тригонометрии - синус (sin), косинус (cos) и тангенс (tg). Они определяются отношениями сторон треугольника.
| Функция | Определение |
|---|---|
| Синус (sin) | Отношение противолежащей стороны к гипотенузе в прямоугольном треугольнике. |
| Косинус (cos) | Отношение прилежащей стороны к гипотенузе в прямоугольном треугольнике. |
| Тангенс (tg) | Отношение синуса косинуса, то есть противолежащей стороны к прилежащей стороне в прямоугольном треугольнике. |
Также существуют обратные функции тригонометрии: арксинус (arcsin), арккосинус (arccos) и арктангенс (arctg), которые позволяют находить углы, соответствующие заданным значениям функций.
Определение области функций тригонометрии
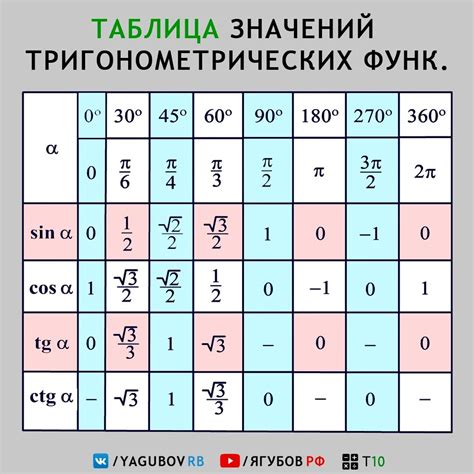
Область функций тригонометрии определяется значениями углов, для которых функции имеют смысл. Основными функциями тригонометрии являются синус (sin), косинус (cos), тангенс (tan), котангенс (cot), секанс (sec) и косеканс (csc).
Для функции синус (sin) и косинус (cos) определены все реальные значения углов. Они изменяются от -1 до 1 и периодически повторяются через каждые 360 градусов (или 2π радиан).
Функции тангенс (tan), котангенс (cot), секанс (sec) и косеканс (csc) имеют ограничения. Тангенс и котангенс имеют периодичность через каждые 180 градусов (или π радиан), а секанс и косеканс - через каждые 360 градусов (или 2π радиан). Кроме того, функции тангенс (tan) и котангенс (cot) имеют особые точки разрыва в значениях углов, где косинус (cos) равен нулю.
Важно учесть, что значения углов могут быть выражены как в радианах, так и в градусах. В зависимости от задачи или контекста, следует использовать соответствующую единицу измерения.
Знание области функций тригонометрии позволяет корректно использовать функции в различных приложениях, а также помогает в понимании свойств и связей между различными функциями.
Правила определения области функций тригонометрии

1. Для функций синус и косинус область определения является множеством всех действительных чисел (-∞, ∞).
2. Для функций тангенс и котангенс область определения не включает значения, при которых косинус равен нулю, то есть множество значений аргумента исключает все точки, где cos(x) = 0. Область определения тангенс и котангенс имеет вид: D = x ≠ (2n + 1)π/2, n ∈ Z.
3. Для функций секанс и косеканс область определения не включает значения, при которых синус равен нулю, то есть множество значений аргумента исключает все точки, где sin(x) = 0. Область определения секанса и косеканса имеет вид: D = x ≠ nπ, n ∈ Z.
4. Для функций арксинус, арккосинус, арктангенс и арккотангенс область определения зависит от значений функции и имеет следующие ограничения:
- Для обратной функции синуса (арксинуса): -1 ≤ y ≤ 1;
- Для обратной функции косинуса (арккосинуса): -1 ≤ y ≤ 1;
- Для обратной функции тангенса (арктангенса): (-∞, ∞);
- Для обратной функции котангенса (арккотангенса): (-∞, ∞).
5. Для функций секанса и косеканса, а также их обратных функций, область определения имеет вид: -1 ≤ y ≤ 1.
Запомните эти правила определения области функций тригонометрии, чтобы корректно использовать и анализировать эти функции в различных математических задачах.
Примеры определения области функций тригонометрии
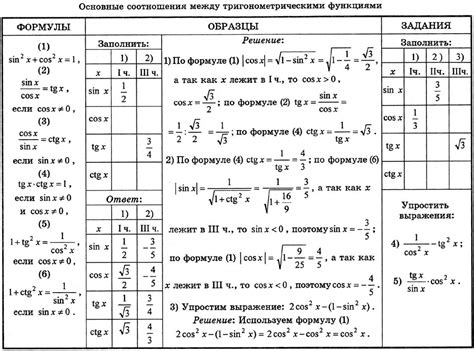
1. Для синуса (sin(x)):
Область определения для синуса охватывает все действительные числа. То есть, любое число может быть аргументом функции sin(x).
2. Для косинуса (cos(x)):
Аналогично синусу, область определения для косинуса также охватывает все действительные числа. Функция cos(x) может принимать любое число в качестве аргумента.
3. Для тангенса (tan(x)):
Область определения функции тангенса ограничена значениями, при которых косинус равен нулю. Деление на ноль не определено, поэтому область определения для тангенса может быть представлена как все действительные числа, за исключением тех, которые являются кратными числу Пи, умноженным на целое число.
4. Для котангенса (cot(x)):
Область определения функции котангенса также ограничена значениями, при которых синус равен нулю. Аналогично тангенсу, область определения для котангенса может быть представлена как все действительные числа, за исключением тех, которые являются кратными числу Пи.
5. Для секанса (sec(x)):
Область определения функции секанса также ограничена значениями, при которых косинус равен нулю. Функция sec(x) может принимать любое действительное число, кроме тех, которые являются кратными числу Пи.
6. Для косеканса (csc(x)):
Область определения функции косеканса ограничена значениями, при которых синус равен нулю. Функция csc(x) может принимать все действительные числа, за исключением тех, которые являются кратными числу Пи.
Изучение областей функций тригонометрии помогает понять, где функция определена и где она принимает свои значения. Это важно при построении графиков и решении уравнений, а также при анализе свойств функций тригонометрии в различных контекстах.
Практическое применение определения области функций тригонометрии

Определение области функций тригонометрии имеет большое практическое значение в различных областях науки и техники. Ниже приведены несколько примеров, где оно применяется:
- Архитектура: При проектировании зданий и сооружений необходимо учитывать особенности распределения нагрузок и напряжений. Функции тригонометрии помогают архитекторам определить оптимальные углы наклона и форму отдельных элементов конструкции.
- Физика: Многие физические явления могут быть описаны с помощью функций тригонометрии. Например, колебания и волны, электрические и магнитные поля, а также движение тела в пространстве. Определение области функций тригонометрии позволяет анализировать эти явления и предсказывать их поведение.
- Инженерия: В различных инженерных расчетах и проектированиях часто требуется анализ углов наклона, например при строительстве дорог, настройке антенн или определении траектории полета ракеты. Функции тригонометрии позволяют сделать точные расчеты и прогнозы.
- Астрономия: В астрономии функции тригонометрии играют значительную роль при определении положения и движения небесных тел. Например, при вычислении координат и орбит планет или при изучении звездных созвездий. Без использования функций тригонометрии точные наблюдения и исследования неба были бы невозможны.
Таким образом, знание и применение определения области функций тригонометрии играют важную роль в решении разнообразных задач, связанных с проектированием, научными исследованиями и практическими приложениями.