Треугольник, в котором две стороны равны друг другу, называется равнобедренным. Это особый вид треугольника, который имеет свои уникальные свойства и особенности. Одной из таких особенностей является равенство углов. В равнобедренном треугольнике два угла, образованные при основании, равны между собой. Это происходит из-за симметрии фигуры и равенства соответствующих сторон.
Правило равенства углов в равнобедренном треугольнике можно доказать по разным путям. Одним из самых простых является использование свойства равности сторон. Если две стороны треугольника равны друг другу, то углы при их основании также окажутся равными. Это следует из определения равенства углов – они равны, если их стороны равны. Таким образом, при равенстве двух сторон автоматически устанавливается равенство углов.
Примером равнобедренного треугольника может служить равносторонний треугольник. У него все стороны равны, а значит, все углы также равны между собой. Также можно взять любой равнобедренный треугольник с неравными сторонами и убедиться, что углы при основании равны. Например, если взять треугольник со сторонами 5, 5 и 8, то при основании 8 будут образовываться равные углы.
Свойства равнобедренного треугольника
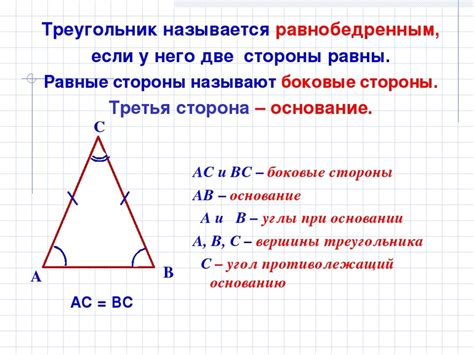
1. Равность боковых сторон.
В равнобедренном треугольнике две боковые стороны равны между собой. Из этого свойства следует, что два угла при основании также равны. Если стороны AB и AC равны, то углы B и C будут равными.
2. Равенство углов при основании.
Если у треугольника две стороны равны, то два угла при основании также равны. В равнобедренном треугольнике углы B и C, образованные при основании, равны друг другу. То есть, если стороны AB и AC равны, углы B и C будут равными, а угол A будет называться вершиной треугольника.
3. Неравные углы.
В равнобедренном треугольнике углы при вершине (угол A) являются неравными. Это происходит из-за того, что фигура образуется при складывании равных углов при основании. Таким образом, углы объединены шейной линией треугольника, к которой присоединяются боковые стороны равными сегментами.
4. Равенство медиан.
Медианы равнобедренного треугольника равны между собой. Медианы – это отрезки, соединяющие вершину треугольника с серединами противоположных сторон. Так как боковые стороны равны, то и середины этих сторон также совпадают, что делает медианы одинаковыми. Таким образом, в равнобедренном треугольнике медианы AB и AC равны.
Равнобедренные треугольники являются специальным случаем в геометрии и имеют свои свойства и особенности, которые могут быть использованы при решении различных задач.
Признаки равенства углов в равнобедренном треугольнике

1. Углы при основании равнобедренного треугольника равны между собой.
- Если две стороны равны, то их углы при основании тоже будут равны.
- Такие углы называются основными углами равнобедренного треугольника.
2. Угол, лежащий напротив равных сторон равнобедренного треугольника, является вершинным углом.
- Вершинный угол равнобедренного треугольника является наибольшим углом в этом треугольнике.
- Он лежит напротив основания и имеет наибольшую меру.
3. Две боковые стороны равнобедренного треугольника равны между собой.
- Это означает, что углы, лежащие противоположно боковым сторонам, также будут равны.
- Такие углы называются боковыми углами равнобедренного треугольника.