Логарифмы – это одно из основных понятий математики, часто встречающееся в различных задачах и уравнениях. Однако, в процессе решения математических задач возникает необходимость выносить минус из логарифма. Это правило является важным инструментом, который позволяет упростить работу с логарифмами и упростить решение уравнений.
Чтобы выносить минус из логарифма, необходимо помнить несколько основных правил. Во-первых, для логарифма с базой a и аргументом x, по свойству логарифма, верно следующее:
loga(x) = -loga(1/x)
Таким образом, если необходимо вынести минус из логарифма, можно изменить знак аргумента и записать его в знаменателе с обратным знаменателю значению.
Давайте рассмотрим примеры применения этого правила. Предположим, необходимо решить уравнение:
log2(x) = -3
В этом случае, применяя правило выноса минуса из логарифма, мы можем записать уравнение следующим образом:
log2(x) = log2(1/8)
Далее, используя основное свойство логарифма loga(ab) = b, мы получаем:
x = 1/8
Таким образом, мы успешно решили уравнение, применяя правило выноса минуса из логарифма.
Что такое логарифм
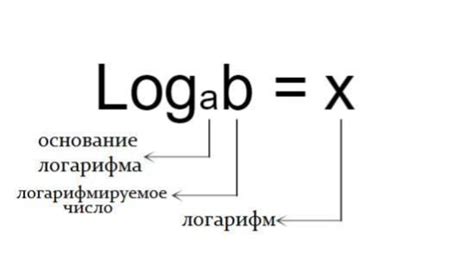
Логарифмы широко применяются в различных областях науки, техники и экономики. В математике они используются для упрощения сложных арифметических операций, а в физике - для решения задач, связанных с экспоненциальным ростом или затуханием.
Логарифмы обладают рядом важных свойств, одно из которых - правило выноса минуса из логарифма. Согласно этому правилу, логарифм отношения двух чисел с минусом равен разности логарифмов этих чисел без знака минус.
| Основание логарифма | Обозначение | Пример |
|---|---|---|
| 10 | lg(x) | lg(100) = 2 |
| 2 | log2(x) | log2(8) = 3 |
| e | ln(x) | ln(e2) = 2 |
Почему нужно выносить минус из логарифма

Почему такая операция имеет смысл? Рассмотрим пример:
logb(a) - это логарифм, которым нужно возвести основание b, чтобы получить а. Если мы умножим это выражение на -1, мы получим:
-logb(a). Теперь основание b возводится в отрицательный логарифм -logb(a), что означает, что речь идет о обратной операции, а именно о нахождении а в качестве основания b. Другими словами, -logb(a) равно 1/a.
Преимущества использования этого правила очевидны. Во-первых, оно позволяет упростить выражения с логарифмами, делая их более компактными и понятными. Во-вторых, правило выноса минуса из логарифма может быть полезным при решении уравнений и неравенств, где применение этого правила может привести к более простому решению.
Важно помнить, что правило выноса минуса из логарифма применимо только к отрицательным логарифмам. Если логарифм положительный, минус не может быть вынесен и остается перед ним.
Использование правила выноса минуса из логарифма может быть очень полезным инструментом в алгебре и математическом анализе, помогая упрощать и решать различные задачи. Оно является основой многих других правил и методов работы с логарифмами.
Как выносить минус из логарифма: практические советы

Для начала, стоит вспомнить основные свойства логарифмов:
- Свойство умножения: loga(b * c) = loga(b) + loga(c)
- Свойство деления: loga(b / c) = loga(b) - loga(c)
- Свойство возведения в степень: loga(bc) = c * loga(b)
- Свойство корня: loga(√b) = 1/2 * loga(b)
Используя эти свойства, можно выносить минус из логарифма по следующему правилу:
Пусть у нас есть выражение loga(-b). Чтобы вынести минус из логарифма, необходимо воспользоваться свойством деления таким образом:
loga(-b) = loga(b / (-1)) = loga(-1) - loga(b)
Таким образом, мы вынесли минус из логарифма и упростили выражение. Теперь можно решать задачи, используя это правило.
Например:
Решим уравнение log2(-x) = 3:
log2(-x) = log2((-1) * x) = log2(-1) - log2(x)
3 = 0 - log2(x)
log2(x) = -3
x = 2-3 = 1/8
Таким образом, мы решили уравнение, используя правило выноса минуса из логарифма.
Примеры выноса минуса из логарифма

Примеры ниже помогут вам лучше понять и запомнить правило выноса минуса из логарифма.
| Пример | Результат |
|---|---|
ln(-x) | ln(x) + iπ |
loga(-x) | loga(x) + iπ/loga(e) |
logb(-y) | logb(y) + iπ/logb(e) |
Здесь i - мнимая единица, а π - число пи. Вынос минуса из логарифма позволяет добавить iπ к результату вычислений.
Обратите внимание, что результат получается в комплексных числах, если исходное значение было отрицательным. Эти примеры созданы для лучшего понимания правила и не являются единственными возможными примерами выноса минуса из логарифма.
Резюме: применение правила выноса минуса из логарифма

Применение данного правила требует аккуратности и точности в рассмотрении выражений с логарифмами. Необходимо учитывать особенности функции логарифма и правила его работы. Правило выноса минуса будет применимо к выражениям, в которых наблюдается деление или умножение логарифмов с одинаковым основанием. Однако, при суммировании или разности логарифмов, данное правило не применимо.
Примером применения правила выноса минуса может служить уравнение вида:
ln(x) - ln(y) = ln(x/y)
Путем выноса отрицательного знака из второго логарифма получим упрощенное выражение и облегчим дальнейшее решение. Это правило также может быть применено к другим типам логарифмов, таким как логарифмы по основанию 10 или другим.
Важно помнить, что правило выноса минуса из логарифма может быть применено только к формулам, содержащим логарифмы с одинаковым основанием и разными аргументами. Также стоит отметить, что при применении данного правила, необходимо быть осторожными в анализе промежуточных итогов и их соответствии действительности.