Как преобразовать шестиугольник в треугольник и пятиугольник

Шестиугольник - одна из разновидностей многоугольников, имеющая шесть сторон и шесть углов. Это геометрическая фигура, которая приманивает своей разносторонностью и сложностью. Однако иногда возникает необходимость преобразовать его в более простые фигуры, такие как треугольник или пятиугольник. В этой статье мы рассмотрим несколько способов преобразования шестиугольника в треугольник и пятиугольник, объясним логику и шаги каждого метода.

Первый способ преобразования шестиугольника в треугольник заключается в удалении двух смежных сторон. Для этого выбираются две другие смежные стороны, и их длины измеряются с использованием линейки или другого геометрического инструмента. Затем эти две стороны отделяются, образуя треугольник внутри шестиугольника. Учтите, что это может привести к изменению формы оставшейся части многоугольника.

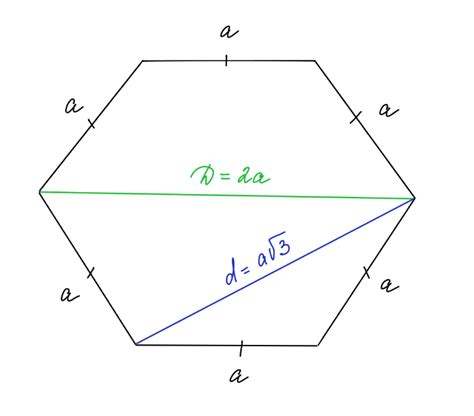
Еще один способ преобразования шестиугольника в треугольник связан с делением двух диагоналей, которые идут от одного угла к другому. Сначала выбираются две диагонали, которые пересекаются внутри шестиугольника. Затем проводится линия, соединяющая точки пересечений этих диагоналей. При этом образуется треугольник, а оставшаяся часть шестиугольника становится пятиугольником. Этот способ требует использования геометрического инструмента для проведения линий и измерения длин.

Важность преобразования шестиугольника в треугольник и пятиугольник

Преобразование шестиугольника в треугольник и пятиугольник имеет большое значение в математике и геометрии. Это позволяет упростить сложные геометрические фигуры, упрощает исследование и анализ их свойств, а также находит практическое применение в различных областях.

Одним из ключевых преимуществ преобразования шестиугольника в треугольник и пятиугольник является уменьшение сложности фигуры. Шестиугольник имеет большее количество углов и сторон, что делает его более сложным для изучения и анализа. После преобразования в треугольник или пятиугольник, фигура становится более простой и легче визуализируется.

Преобразование шестиугольника в треугольник и пятиугольник также имеет практическое применение. Например, в строительстве и дизайне, треугольники и пятиугольники часто используются для создания устойчивых и эстетически приятных конструкций. Они обладают особыми свойствами, которые делают их предпочтительными для определенных задач.

Кроме того, преобразование шестиугольника в треугольник и пятиугольник помогает углубить понимание геометрии и математических концепций. Изучение свойств этих преобразований позволяет лучше разобраться в принципах и законах геометрии, а также способствует развитию аналитического мышления и решению сложных геометрических задач.

Математическое преобразование шестиугольника в треугольник и пятиугольник

Шестиугольник – это выпуклая фигура, которая имеет шесть сторон и шесть углов. Процесс преобразования шестиугольника в треугольник и пятиугольник основан на изменении количества сторон и углов данной фигуры.

Чтобы преобразовать шестиугольник в треугольник, достаточно отсечь одну из его сторон. Таким образом, шестиугольник превращается в пятиугольник с одной стороной меньше. Далее, можно отсечь еще одну сторону пятиугольника и получить уже треугольник.

Пример преобразования шестиугольника в треугольник:

Шестиугольник	Пятиугольник	Треугольник

Таким образом, математическое преобразование шестиугольника в треугольник и пятиугольник осуществляется путем последовательного отсечения сторон заданной фигуры.

Преобразование геометрических фигур является важным инструментом в математике и может применяться для решения различных задач и построения композиций. Вышеописанный метод преобразования позволяет упростить фигуру, уменьшить количество боковых ребер и углов до требуемого количества.

Геометрическое преобразование шестиугольника в треугольник и пятиугольник

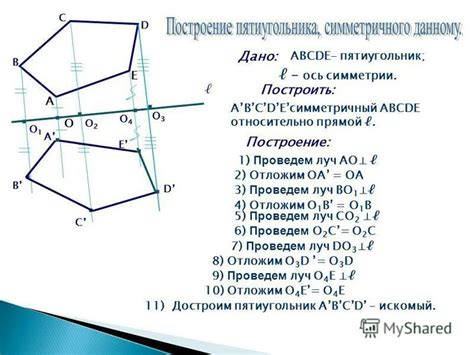
Для того чтобы преобразовать шестиугольник в треугольник, нужно провести от одного из углов диагональ в противоположный угол. Таким образом, получится треугольник, состоящий из двух сторон шестиугольника и одной диагонали.

Если требуется преобразовать шестиугольник в пятиугольник, то нужно удалить одну из его сторон. Для этого можно, например, провести линию от одного из углов внутрь фигуры и удалить одну из сторон, получив пятиугольник, состоящий из пяти сторон шестиугольника.

Геометрические преобразования являются важным инструментом при решении различных задач в геометрии. Они позволяют менять форму и структуру фигур, делая их более подходящими для конкретных задач или приводя их к более простым формам для упрощения вычислений.

Практическое применение преобразования шестиугольника в треугольник и пятиугольник

Одним из практических применений этого преобразования является дизайн архитектурных конструкций. Замена сложных шестиугольников на треугольники и пятиугольники позволяет упростить конструкцию и делает ее более стабильной и прочной. Это особенно важно при проектировании куполов, каркасов и других сложных форм.

Еще одним практическим применением является создание уникальных узоров и рисунков. Преобразование шестиугольника позволяет создавать разнообразные геометрические фигуры, которые могут использоваться для декоративного оформления предметов и поверхностей. Такие узоры могут быть использованы в интерьерном дизайне, текстильной промышленности и других областях искусства.

Кроме того, преобразование шестиугольника в треугольник и пятиугольник широко применяется в компьютерной графике и алгоритмах визуализации. Это позволяет упростить расчеты и ускорить процесс отображения геометрических объектов. Преобразование также может быть использовано для сжатия данных и оптимизации алгоритмов.

Таким образом, преобразование шестиугольника в треугольник и пятиугольник имеет широкое практическое применение в различных областях. Оно позволяет упростить сложные формы, повысить стабильность и прочность конструкций, создавать уникальные узоры и оптимизировать алгоритмы. Это делает преобразование неотъемлемой частью геометрии и компьютерных наук.

1. Уменьшение количества сторон

Преобразование шестиугольника в треугольник и пятиугольник предполагает уменьшение количества сторон полигона. В результате этого процесса, шестиугольник, состоящий из шести сторон, превращается в треугольник с тремя сторонами или пятиугольник с пятью сторонами. Это показывает, что преобразование изменяет не только форму полигона, но и его геометрические свойства.

2. Изменение углов

Преобразование шестиугольника в треугольник и пятиугольник также изменяет значения углов полигона. В шестиугольнике углы могут быть равными или различными, в зависимости от его конкретной формы. Однако при преобразовании шестиугольника в треугольник или пятиугольник, значения углов изменятся, так как полигон будет иметь меньшее количество сторон. Это может привести к изменению пропорций углов и внешнего вида полигона.

3. Изменение площади

Преобразование шестиугольника в треугольник или пятиугольник также влияет на его площадь. Шестиугольник с большим количеством сторон, как правило, имеет большую площадь по сравнению с треугольником или пятиугольником. Поэтому преобразование может привести к уменьшению площади полигона. Это может быть полезно в различных математических задачах, требующих работы с полигонами различных форм и площадей.