Теорема Пифагора - одна из самых известных и полезных формул в геометрии. Она устанавливает взаимосвязь между длинами сторон прямоугольного треугольника. Но мало кто знает, что теорема Пифагора также может быть применена и в других типах треугольников, таких как равнобедренный.
Равнобедренный треугольник имеет две равные стороны и две равные углы. При этом, третья сторона, называемая основанием, будет отличаться от остальных двух. Используя теорему Пифагора, можно найти длину основания, зная длины равных сторон.
Формула теоремы Пифагора выглядит следующим образом: а2 = b2 + c2, где а - это основание равнобедренного треугольника, b и c - равные стороны.
Равнобедренный треугольник: определение и свойства
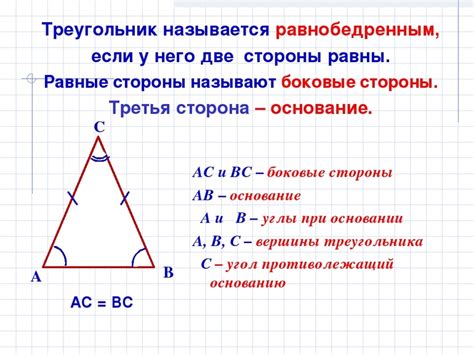
Основные свойства равнобедренного треугольника:
- Основания равнобедренного треугольника - это две равные стороны, которые лежат против одного и того же угла.
- Углы при основаниях равнобедренного треугольника равны.
- Высота, проведенная из вершины равнобедренного треугольника, делит его на два прямоугольных треугольника, с равными гипотенузами.
- Медиана и биссектриса, проведенные из вершины равнобедренного треугольника, являются одновременно высотами.
- Периметр равнобедренного треугольника можно найти по формуле:
P = 2a + b, гдеa- длина основания,b- длина боковой стороны. - Площадь равнобедренного треугольника можно найти по формуле:
S = (1/2)ah, гдеа- длина основания,h- высота, проведенная из вершины равнобедренного треугольника.
Равнобедренные треугольники широко используются в геометрии и в реальной жизни. Они встречаются в архитектуре, инженерии, при решении задач физики и многих других областях науки. Понимание свойств равнобедренных треугольников помогает упростить решение задач и получение более точных результатов.
Теорема Пифагора и ее формула
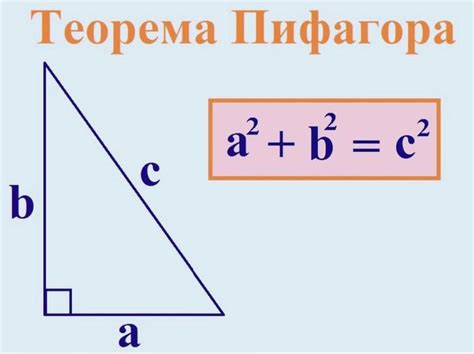
Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов:
c² = a² + b²
где c - длина гипотенузы, а и b - длины катетов треугольника.
Эта теорема может быть использована не только для обычных прямоугольных треугольников, но и для равнобедренных треугольников.
Формула теоремы Пифагора позволяет находить длину неизвестной стороны прямоугольного треугольника, если известны длины двух других сторон. Также она часто применяется в решении различных задач с применением геометрических доказательств.
Например, рассмотрим равнобедренный треугольник со сторонами a = 5 см, b = 5 см и гипотенузой c. Используя теорему Пифагора, мы можем найти значение c:
c² = a² + b²
c² = 5² + 5² = 25 + 25 = 50
c = √50 ≈ 7.07 см
Таким образом, длина гипотенузы равнобедренного треугольника составляет около 7.07 см.
Теорема Пифагора и ее формула являются одной из основных концепций в геометрии и находят широкое применение в различных областях, где требуется работа с прямоугольными треугольниками.
Применение теоремы Пифагора в равнобедренных треугольниках
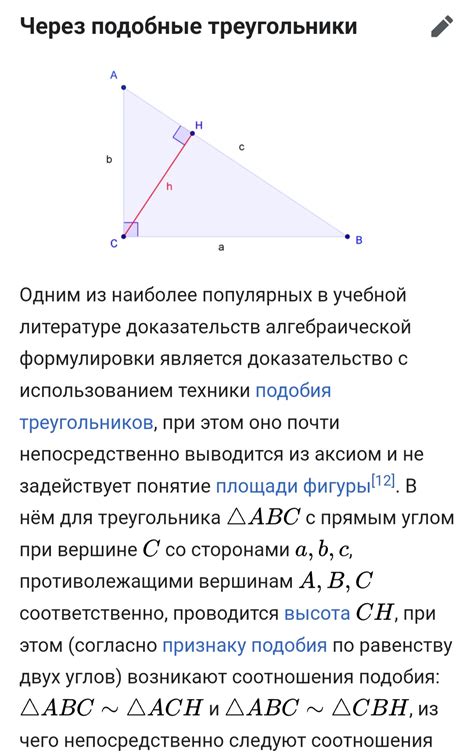
Казалось бы, эта теорема применяется только в прямоугольных треугольниках. Однако, теорема Пифагора также находит свое применение и в других типах треугольников, например в равнобедренных треугольниках.
Равнобедренный треугольник - это треугольник, у которого две стороны равны. Из этого свойства следует, что два угла треугольника также равны. Рассмотрим равнобедренный треугольник ABC, в котором AB=AC.
Согласно теореме Пифагора, квадрат гипотенузы треугольника равен сумме квадратов катетов. В случае равнобедренного треугольника, гипотенузой является основание треугольника (сторона BC), а катетами - боковые стороны треугольника (стороны AB и AC).
Таким образом, формула для применения теоремы Пифагора в равнобедренных треугольниках выглядит следующим образом:
| Квадрат гипотенузы | = | Квадрат катета | + | Квадрат катета |
|---|---|---|---|---|
| BC2 | = | AB2 | + | AC2 |
Пример: Рассмотрим равнобедренный треугольник со сторонами длиной 5. Зная, что две стороны равны, мы можем применить теорему Пифагора:
| Квадрат гипотенузы | = | Квадрат катета | + | Квадрат катета |
|---|---|---|---|---|
| BC2 | = | AB2 | + | AC2 |
| BC2 | = | 52 | + | 52 |
| BC2 | = | 25 | + | 25 |
| BC2 | = | 50 |
Из примера видно, что квадрат гипотенузы равнобедренного треугольника равен 50. Для нахождения длины гипотенузы необходимо извлечь квадратный корень из этого значения.
Применение теоремы Пифагора в равнобедренных треугольниках позволяет находить значения длин сторон треугольника, используя только известные значения.
Как найти длину основания равнобедренного треугольника с использованием теоремы Пифагора
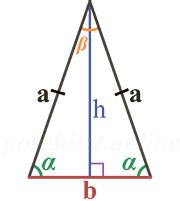
Для нахождения длины основания равнобедренного треугольника можно использовать теорему Пифагора, которая устанавливает связь между длинами сторон треугольника и длиной его гипотенузы.
Допустим, что в равнобедренном треугольнике известны длина одной из сторон (сторона равна a) и длина гипотенузы (длина гипотенузы равна c). Чтобы найти длину основания (сторона b), можно воспользоваться теоремой Пифагора:
c^2 = a^2 + b^2
Для этого нужно возвести в квадрат длины основания (b), сложить этот квадрат с квадратом длины стороны (a) и сравнить полученную сумму с квадратом длины гипотенузы (c^2). Затем из полученного уравнения можно найти длину основания (b).
Например, если известны длина стороны (a) равна 4 и длина гипотенузы (c) равна 5, то можно решить уравнение следующим образом:
5^2 = 4^2 + b^2
25 = 16 + b^2
9 = b^2
b = 3
Итак, длина основания равнобедренного треугольника равна 3.
Примеры решений задач с применением теоремы Пифагора в равнобедренных треугольниках
Пример 1:
Дан равнобедренный треугольник ABC, в котором стороны AB и AC равны 6 см. Найдем длину основания BC.
Решение:
Из свойств равнобедренного треугольника мы знаем, что высота, опущенная из вершины А на основание ВС, является медианой и биссектрисой. Так как треугольник равнобедренный, то высота разделит основание на две равные части.
Используем теорему Пифагора:
BC^2 = AC^2 - AB^2 = 6^2 - 6^2 = 0
Таким образом, длина основания BC равна 0.
Пример 2:
Дан равнобедренный треугольник PQR, в котором стороны PQ и PR равны 12 см. Найдем длину медианы PM, где M - середина стороны QR.
Решение:
Используем свойства равнобедренного треугольника: медиана, проведенная из вершины, делит противолежащую сторону пополам.
Таким образом, длина медианы PM равна половине длины стороны QR:
PM = QR/2 = 12/2 = 6 см.
Таким образом, длина медианы PM равна 6 см.
Задачи для самостоятельного решения с применением теоремы Пифагора в равнобедренных треугольниках

Если a и b – равными сторонами правильного треугольника, а c – гипотенуза, то с помощью теоремы Пифагора данную геометрическую форму можно записать следующим образом:
\(a^2 + b^2 = c^2\).
Используя данную формулу, теперь можем перейти к решению задач:
- В равнобедренном треугольнике одна сторона равна 10 см. Найдите длину гипотенузы.
- В треугольнике ABC сторона AB равна 7 см, а сторона BC равна 9 см. Найдите длину гипотенузы треугольника ABC.
- В равнобедренном треугольнике одна сторона равна 12 см, а гипотенуза равна 15 см. Найдите длину второй стороны.
Пользуясь формулой теоремы Пифагора в равнобедренных треугольниках, можно решить данные задачи и получить ответы, зная длины сторон треугольников.