Расчет второй производной функции играет важную роль в математике и науке в целом. Он позволяет определить, как функция меняется со временем или в пространстве. В этой статье мы рассмотрим основные принципы расчета второй производной и рассмотрим несколько примеров, чтобы лучше понять этот процесс.
Вторая производная функции определяет, каким образом меняется скорость изменения функции. Она позволяет исследовать выпуклость и вогнутость функции и находить экстремумы. Расчет второй производной может быть сложным процессом, но с помощью определенных методов и формул он становится более понятным и доступным.
Для расчета второй производной функции можно использовать такие методы, как метод дифференцирования, методы численного дифференцирования и методы символьного дифференцирования. Каждый из этих методов имеет свои особенности и подходит для определенных задач. В данной статье мы рассмотрим примеры применения этих методов на практике и подробно расскажем о каждом из них.
Метод дифференцирования - один из наиболее распространенных методов расчета второй производной функции. Он основан на применении правила дифференцирования функции для поиска ее производной. Зная первую производную функции, мы можем построить уравнение для второй производной и решить его. Этот метод требует хорошего знания математических правил и формул дифференцирования, но при правильном применении он может значительно упростить расчет второй производной.
Примеры расчета второй производной функции

Расчет второй производной функции может быть полезен для определения существования экстремумов, определения выпуклости и вогнутости графика функции, а также для анализа поведения функции в различных точках. Приведем некоторые примеры расчета второй производной функции.
Рассмотрим функцию f(x) = x^3 - 4x^2 + 3x - 2. Для расчета второй производной функции, сначала найдем ее первую производную:
f'(x) = 3x^2 - 8x + 3.
Затем найдем вторую производную функции:
f''(x) = 6x - 8.
Таким образом, вторая производная функции f(x) равна f''(x) = 6x - 8.
Рассмотрим функцию g(x) = sin(x) + cos(x). Для расчета второй производной функции, найдем ее первую производную:
g'(x) = cos(x) - sin(x).
Затем найдем вторую производную функции:
g''(x) = -sin(x) - cos(x).
Таким образом, вторая производная функции g(x) равна g''(x) = -sin(x) - cos(x).
Рассмотрим функцию h(x) = e^x. Для расчета второй производной функции, найдем ее первую производную:
h'(x) = e^x.
Затем найдем вторую производную функции:
h''(x) = e^x.
Таким образом, вторая производная функции h(x) равна h''(x) = e^x.
Вторая производная функции позволяет более подробно исследовать ее свойства и выявлять особенности поведения графика функции в различных точках. Расчет второй производной может быть полезным в различных областях науки и техники, где требуется анализ и оптимизация функций.
Методы нахождения второй производной функции

Вторая производная функции играет важную роль в анализе и оптимизации функций. Она позволяет определить изменение темпа роста функции и отыскать точки экстремума.
Существует несколько методов нахождения второй производной функции:
- Аналитический метод. Для некоторых функций, можно легко вычислить вторую производную с помощью соответствующих правил дифференцирования. Например, для многочлена n-ой степени, вторая производная будет многочленом степени (n-2).
- Метод численного дифференцирования. Если аналитическое вычисление второй производной сложно или невозможно, можно приближенно вычислить ее численно. Существует несколько методов численного дифференцирования, таких как метод конечных разностей и метод симметричных разностей.
- Использование специализированного программного обеспечения. Существуют программы, которые автоматически могут вычислить производные функций, включая вторую производную. Такие программы могут быть полезны, особенно при наличии сложных или параметрических функций.
Выбор метода нахождения второй производной функции зависит от ее аналитической формы, сложности вычислений и доступности программного обеспечения. Знание и умение применять все эти методы позволяет проводить более глубокий анализ функций и использовать их для решения различных задач в науке и инженерии.
Алгоритмы для вычисления второй производной функции

Одним из наиболее простых алгоритмов для вычисления второй производной функции является метод дифференцирования дважды. Сначала применяется первый производный для получения новой функции, а затем к ней применяется дифференцирование снова. Этот метод может быть применим в случаях, когда функция имеет аналитическое выражение или когда есть возможность выполнить дифференцирование вручную.
Еще одним популярным методом вычисления второй производной функции является использование численных методов, таких как метод конечной разности. Этот метод основывается на аппроксимации производной с использованием конечных разностей. Путем применения аппроксимации для первой производной и затем повторного применения этой аппроксимации можно получить приближенное значение второй производной.
Другие методы для вычисления второй производной функции включают использование специализированных алгоритмов, таких как метод Де Бура, который позволяет вычислять численные значения высокой точности. Кроме того, можно использовать численные библиотеки и программное обеспечение, которые предоставляют функции для вычисления второй производной.
При выборе алгоритма для вычисления второй производной функции важно учитывать как его эффективность, так и точность результата. Некоторые методы могут быть более подходящими для определенных типов функций или для определенного диапазона значений. Также важно учитывать возможность ошибок округления при использовании численных методов.
Кроме того, при вычислении второй производной функции рекомендуется использовать численные методы с высокой точностью, особенно если результат будет использоваться в дальнейшем анализе или моделировании. Точные вычисления могут быть критически важными при принятии решений на основе результатов анализа. Поэтому выбор правильного алгоритма и метода вычисления второй производной функции необходимо осуществлять внимательно и с учетом всех факторов.
Покоординатные формулы для определения второй производной функции
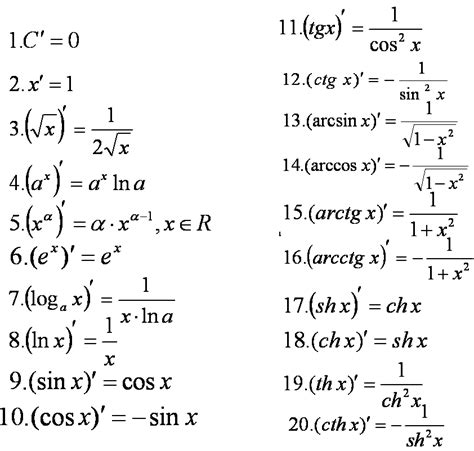
Покоординатные формулы обычно применяются, когда функция задана в виде суммы нескольких функций. В этом случае первую и вторую производные каждой функции можно вычислить отдельно, а затем сложить соответствующие части. Такой подход позволяет упростить расчеты и получить более точные результаты.
Вторая производная функции f(x, y) может быть выражена следующим образом:
- По переменной x:
f_{xx}(x, y) = \frac{{\partial^2 f}}{{\partial x^2}} - По переменной y:
f_{yy}(x, y) = \frac{{\partial^2 f}}{{\partial y^2}} - По переменным x и y:
f_{xy}(x, y) = \frac{{\partial^2 f}}{{\partial x \partial y}} - По переменным y и x:
f_{yx}(x, y) = \frac{{\partial^2 f}}{{\partial y \partial x}}
Для функции с более чем двумя переменными количество покоординатных формул увеличивается соответственно. Однако основная идея остается неизменной: вычислить все вторые производные отдельно и суммировать соответствующие части.
Использование покоординатных формул для вычисления второй производной функции упрощает анализ и позволяет получить более полное представление о её свойствах. Однако стоит помнить, что этот метод может быть достаточно трудоемким при вычислениях вручную. Поэтому при необходимости часто применяют численные методы, такие как метод конечных разностей или метод конечных элементов.
Применение второй производной функции в задачах о выпуклости и вогнутости

Функция называется выпуклой на некотором интервале, если ее вторая производная положительна на этом интервале. Иными словами, график функции будет выпуклым вверх. Примером может служить функция f(x) = x^2, которая является выпуклой на всей числовой прямой.
С другой стороны, функция называется вогнутой на некотором интервале, если ее вторая производная отрицательна на этом интервале. То есть, график функции будет вогнутым вниз. Например, функция f(x) = -x^2 будет вогнутой на всей числовой прямой.
Знание о выпуклости и вогнутости функции имеет практическое применение в различных областях:
- В экономике и финансах, выпуклые функции используются при определении оптимальных решений, максимизации прибыли и минимизации затрат;
- В физике и инженерии, при анализе свойств кривых и поверхностей;
- В оптимизационных задачах и математическом программировании, где необходимо найти экстремальные значения функции.
Расчет второй производной функции может быть выполнен вручную или с использованием компьютерных программ и алгоритмов. Полученные значения можно использовать для определения точек выпуклости и вогнутости функции, а также для нахождения экстремумов и точек перегиба.
Расчет второй производной функции путем дифференцирования

Вторая производная функции представляет собой производную от первой производной. То есть это производная производной функции. Расчет второй производной функции позволяет определить изменение скорости изменения функции в заданной точке.
Существует несколько методов расчета второй производной функции. Один из них - дифференцирование. Для этого необходимо выполнить два последовательных дифференцирования исходной функции.
Рассмотрим пример. Дана функция y = f(x) = 3x^2 + 2x - 1. Для расчета второй производной функции f(x) путем дифференцирования, сначала найдем первую производную, а затем найдем ее производную.
1. Найдем первую производную функции f(x):
| f(x) | f'(x) |
|---|---|
| 3x^2 + 2x - 1 | 6x + 2 |
2. Теперь найдем вторую производную функции f(x), дифференцируя первую производную:
| f'(x) | f''(x) |
|---|---|
| 6x + 2 | 6 |
Таким образом, вторая производная функции f(x) равна 6.
Расчет второй производной функции путем дифференцирования позволяет определить, как меняется угол наклона касательной к графику функции в заданной точке. Эта информация может быть полезной при исследовании поведения функции на определенном участке.
Полезные советы при расчете второй производной функции

1. Правило Лейбница: вторая производная функции f(x) равна производной ее первой производной. Для вычисления второй производной необходимо сначала найти первую производную и затем продифференцировать ее снова.
2. Обратите внимание на знаки: знак второй производной может дать информацию о форме функции и наличии экстремумов. Если вторая производная положительна, то функция выпукла вверх и имеет локальный минимум. Если вторая производная отрицательна, то функция выпукла вниз и имеет локальный максимум.
3. В случае, если вторая производная равна нулю, это может указывать на точку перегиба функции. Однако, необходимо учесть, что это условие является необязательным и должно дополняться анализом первой производной и значением функции в окрестности.
4. Используйте таблицы для организации данных: при расчете второй производной функции может потребоваться выполнение множества шагов и обработка большего количества данных. В данном случае использование таблицы позволяет упорядочить и систематизировать информацию, что упрощает процесс и уменьшает вероятность ошибок.
| Шаг | Функция | Первая производная | Вторая производная |
|---|---|---|---|
| 1 | f(x) | f'(x) | f''(x) |
| 2 | ... | ... | ... |
| N | ... | ... | ... |
5. Проверяйте результаты с использованием других методов: расчет второй производной функции может быть сложным и подверженным ошибкам. Поэтому рекомендуется проверять полученные результаты с использованием альтернативных методов, например, с использованием численных методов дифференцирования.
Надеемся, что эти полезные советы помогут вам в расчете второй производной функции и повысят точность ваших результатов. Удачи в ваших исследованиях и анализе функций!