Быстрая сортировка, также известная как сортировка Хоара, является одним из самых эффективных алгоритмов сортировки, широко применяемых в языке программирования Java. Она основывается на принципе "разделяй и властвуй", что позволяет сортировать массивы или списки данных очень быстро и эффективно. Главное преимущество быстрой сортировки заключается в том, что она работает в среднем случае за время O(n log n).
Принцип работы быстрой сортировки заключается в том, чтобы выбрать опорный элемент из массива данных, затем разделить массив на две части: одна часть будет содержать элементы, меньшие опорного, другая - элементы, большие опорного. Затем процесс разделения рекурсивно повторяется для каждой части массива, пока части не будут содержать только один элемент или будут пустыми. После этого части объединяются в отсортированный массив.
Алгоритм можно представить в следующем виде:
- Выбрать опорный элемент из массива данных.
- Разделить массив на две части: элементы, меньшие опорного, и элементы, большие опорного.
- Рекурсивно применить алгоритм к каждой части массива до тех пор, пока части не будут содержать только один элемент или будут пустыми.
- Объединить части в отсортированный массив.
Быстрая сортировка позволяет сортировать большие объемы данных с высокой скоростью. В языке программирования Java доступны различные реализации этого алгоритма, которые могут быть использованы в зависимости от конкретной задачи и требований проекта.
Принципы быстрой сортировки в Java

Принцип работы быстрой сортировки в Java заключается в выборе опорного элемента из массива и перемещении всех элементов, меньших опорного, влево от него, а всех элементов, больших опорного, - вправо. После этого рекурсивно вызывается алгоритм для каждой из получившихся частей, пока в них не останется по одному элементу, что является базовым случаем.
Выбор опорного элемента играет важнейшую роль в эффективности алгоритма. Обычно в качестве опорного элемента выбирается серединный элемент или среднее значение первого, последнего и срединного элементов. Однако, если массив уже отсортирован или содержит много повторяющихся элементов, это может привести к неоптимальным результатам. В таких случаях можно использовать другие методы выбора опорного элемента, например, случайный элемент или медиану трех элементов.
В процессе выполнения алгоритма быстрой сортировки происходит сравнение и перемещение элементов массива, что делает его ин-плейс алгоритмом сортировки. Это означает, что он не требует дополнительной памяти для выполнения сортировки и может работать с массивами любого размера.
Быстрая сортировка обладает высокой производительностью и эффективностью в большинстве случаев, но в худшем случае может иметь квадратичную сложность времени. Однако существуют различные оптимизации алгоритма, которые позволяют снизить вероятность возникновения худшего случая и ускорить его работу.
Работа алгоритма быстрой сортировки
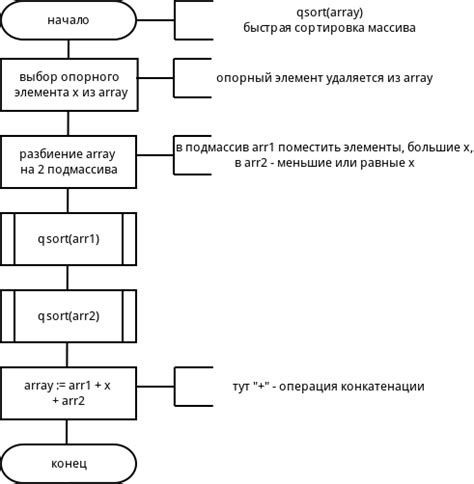
- Выбор опорного элемента
- Разделение массива
- Рекурсивное применение алгоритма
- Слияние отсортированных массивов
Вначале алгоритма выбирается опорный элемент из массива. Опорный элемент может быть выбран случайным образом или по определенному критерию, например, средний элемент массива.
Затем массив разделяется на две части - одна содержит элементы, меньшие опорного, а другая - элементы, большие опорного. Для этого используется процедура разделения (Partition), которая перемещает элементы так, чтобы все элементы меньше опорного были слева от него, а все элементы больше опорного - справа.
После разделения массива, алгоритм рекурсивно применяется к обоим половинам массива. То есть, сначала быстрая сортировка применяется к левой половине массива, затем - к правой половине.
В конце алгоритма, когда размеры подмассивов становятся достаточно маленькими, чтобы быть отсортированными, происходит их слияние. Это достигается путем объединения отсортированных частей массива в один отсортированный массив.
Алгоритм быстрой сортировки обладает высокой эффективностью (O(n log n) в среднем случае) и устойчивостью к входным данным. Однако, в худшем случае (если масив уже отсортирован или содержит большое количество повторяющихся элементов) алгоритм может работать долго и требовать большого количества дополнительной памяти.
Примеры применения быстрой сортировки в Java

Сортировка массива чисел:
public class QuickSort {
public static void quickSort(int[] arr, int low, int high) {
if (low < high) {
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
public static int partition(int[] arr, int low, int high) {
int pivot = arr[high];
int i = (low - 1);
for (int j = low; j < high; j++) {
if (arr[j] < pivot) {
i++;
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
int temp = arr[i + 1];
arr[i + 1] = arr[high];
arr[high] = temp;
return i + 1;
}
public static void main(String[] args) {
int[] arr = {10, 7, 8, 9, 1, 5};
int n = arr.length;
quickSort(arr, 0, n - 1);
System.out.println("Отсортированный массив:");
for (int i = 0; i < n; i++) {
System.out.print(arr[i] + " ");
}
}
}
Сортировка списка объектов:
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class QuickSort {
public static void quickSort(List<Integer> list, int start, int end) {
if (start < end) {
int pivotIndex = partition(list, start, end);
quickSort(list, start, pivotIndex - 1);
quickSort(list, pivotIndex + 1, end);
}
}
public static int partition(List<Integer> list, int start, int end) {
int pivot = list.get(end);
int i = start - 1;
for (int j = start; j < end; j++) {
if (list.get(j) < pivot) {
i++;
int temp = list.get(i);
list.set(i, list.get(j));
list.set(j, temp);
}
}
int temp = list.get(i + 1);
list.set(i + 1, list.get(end));
list.set(end, temp);
return i + 1;
}
public static void main(String[] args) {
List<Integer> list = new ArrayList<>(Arrays.asList(10, 7, 8, 9, 1, 5));
int n = list.size();
quickSort(list, 0, n - 1);
System.out.println("Отсортированный список:");
for (int i = 0; i < n; i++) {
System.out.print(list.get(i) + " ");
}
}
}
Сортировка массива объектов:
import java.util.Arrays;
public class QuickSort {
public static void quickSort(Student[] arr, int low, int high) {
if (low < high) {
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
public static int partition(Student[] arr, int low, int high) {
Student pivot = arr[high];
int i = low - 1;
for (int j = low; j < high; j++) {
if (arr[j].getAge() < pivot.getAge()) {
i++;
Student temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
Student temp = arr[i + 1];
arr[i + 1] = arr[high];
arr[high] = temp;
return i + 1;
}
public static void main(String[] args) {
Student[] arr = {new Student("Alice", 20), new Student("Bob", 18), new Student("Charlie", 22)};
int n = arr.length;
quickSort(arr, 0, n - 1);
System.out.println("Отсортированный массив объектов:");
for (int i = 0; i < n; i++) {
System.out.println(arr[i].getName() + " " + arr[i].getAge());
}
}
}
class Student {
private String name;
private int age;
public Student(String name, int age) {
this.name = name;
this.age = age;
}
public String getName() {
return name;
}
public int getAge() {
return age;
}
}
Это лишь небольшая часть возможных применений быстрой сортировки в Java. Алгоритм легко можно адаптировать для работы с различными типами данных, объектами и структурами. Быстрая сортировка обладает высокой эффективностью и является отличным выбором для решения задач сортировки в Java программировании.
Особенности и объяснение быстрой сортировки в Java
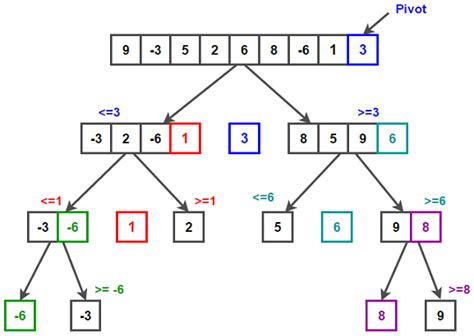
Основная идея быстрой сортировки заключается в разделении массива на более мелкие части и их последующей сортировке. Этот процесс называется «разделение и властвование». Алгоритм выбирает один элемент массива, называемый осью, и перемещает все элементы, меньшие оси, влево от нее, а все элементы, большие оси, - вправо от нее. Затем алгоритм рекурсивно применяется к двум подмассивам слева и справа от оси, пока весь массив не будет отсортирован.
Одна из особенностей быстрой сортировки в Java состоит в том, что она имеет лучший средний случай сортировки с временной сложностью O(n log n). Оптимальный выбор оси и эффективные алгоритмы разделения позволяют достичь такой высокой производительности.
Однако быстрая сортировка также имеет некоторые недостатки. В худшем случае, когда ось выбирается неоптимальным образом, временная сложность может составить O(n^2). Кроме того, алгоритм работает не на всех типах данных, например, на списке связанных элементов с большой глубиной рекурсии быстрая сортировка может стать неэффективной из-за нехватки стека вызова.