Генератор случайных чисел (ГСЧ) – это непрерывно развивающаяся область, которая находит широкое применение в различных отраслях, включая компьютерные игры, статистику и развлекательные мероприятия, такие как розыгрыши призов. ГСЧ создает результаты, которые кажутся случайными, но на самом деле базируются на определенных алгоритмах и формулах.
Реалистичность и непредсказуемость результатов генератора случайных чисел крайне важны для его успешного использования в розыгрышах. Чтобы достичь этого, разработчики используют различные методы и источники данных для начальных значений в алгоритмах ГСЧ. Одним из основных методов является использование системного времени в качестве начального значения или "семени". Это значение обеспечивает уникальность и исключает возможность повторения последовательностей, что делает результаты непредсказуемыми и случайными.
Важно отметить, что генератор случайных чисел работает на основе математических операций и позволяет получать длинные последовательности случайных чисел. С помощью различных алгоритмов, таких как линейный конгруэнтный метод или метод Мерсенна-Твистера, разработчики могут создавать последовательности чисел, которые кажутся случайными пользователю, но на самом деле определены определенными математическими формулами.
Важно понимать, что генератор случайных чисел может создавать лишь псевдослучайные числа, то есть числа, которые выглядят случайными, но на самом деле являются результатом определенных алгоритмов. Несмотря на это, современные ГСЧ обладают высокой степенью непредсказуемости, что делает их идеальным инструментом для использования в розыгрышах и других ситуациях, где требуется неискаженность и случайность результатов.
Принцип работы генератора случайных чисел
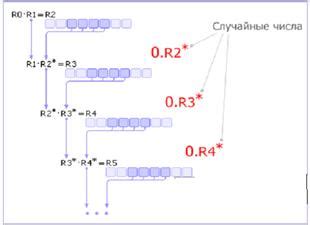
Одним из самых распространенных алгоритмов ГСЧ является алгоритм на основе псевдослучайных чисел. В этом случае, ГСЧ начинает свою работу с некоторого начального значения, называемого зерном. Затем, путем применения определенных математических операций к зерну, генерируется последовательность чисел.
Важной характеристикой генератора случайных чисел является его периодичность. Период - это количество чисел, которое генератор способен сгенерировать перед тем, как начнется повторение последовательности. Чем больше период, тем лучше генератор с точки зрения случайности его результатов.
Однако полностью случайные числа невозможно сгенерировать с помощью алгоритма, так как они основаны на определенных математических или физических процессах. Тем не менее, псевдослучайные числа обладают свойством, близким к случайному, и могут быть использованы для создания разнообразных случайных сценариев, таких как розыгрыши, шифрование данных и моделирование случайных событий.
У генераторов случайных чисел есть свои ограничения и слабые стороны. Например, если зерно генератора известно, то можно воссоздать всю последовательность чисел и предсказать будущие значения. Также, если алгоритм ГСЧ не имеет достаточно хорошего периода, то результаты могут начать повторяться после некоторого времени, что может привести к ухудшению качества использования генератора.
Тем не менее, генераторы случайных чисел широко используются во многих областях, требующих случайных значений, и их принцип работы является важным аспектом для понимания возможностей и ограничений таких алгоритмов.
Основные понятия и принципы работы

Семя генератора - это исходное число или набор чисел, которые используются для инициализации ГСЧ. От выбранного семени зависит последовательность случайных чисел, которую ГСЧ будет генерировать. Для розыгрышей обычно используется текущее время в качестве семени, чтобы получать каждый раз новую последовательность чисел.
Алгоритм генерации случайных чисел - это математическая формула или процедура, которая определяет, какие числа будут генерироваться на основе семени. Существует множество различных алгоритмов, но все они должны обладать свойствами случайности, равномерности и независимости. Например, одним из популярных алгоритмов является линейный конгруэнтный метод.
Период генератора - это количество уникальных случайных чисел, которые может сгенерировать ГСЧ перед тем, как он начнет повторять свою последовательность. Чем больше период, тем лучше, потому что повторение последовательности может привести к предсказуемым результатам.
Псевдослучайность - это свойство ГСЧ, которое означает, что последовательность чисел, которые он генерирует, выглядит случайной, но на самом деле является детерминированной. То есть, если семя и алгоритм генерации известны, то можно предсказать результаты ГСЧ. Однако, для большинства целей, псевдослучайность является достаточно хорошим приближением случайности.
Использование ГСЧ для розыгрыша - для проведения розыгрыша, ГСЧ используется для генерации случайного числа или набора чисел, которые выбирают победителя или определяют другие случайные события. Благодаря своей псевдослучайности, ГСЧ позволяет создать непредсказуемую и справедливую ситуацию для всех участников.
Важно отметить, что хорошо спроектированный и реализованный генератор случайных чисел обеспечивает высокую степень случайности и непредсказуемости для использования в розыгрышах и других приложениях, где важна случайность результатов.
Виды генераторов случайных чисел
Алгоритмические генераторы
Алгоритмические генераторы работают путем применения определенного алгоритма для генерации последовательности чисел, которая кажется случайной. Они наиболее часто используются в компьютерных программных системах.
В алгоритмических генераторах случайных чисел начальное число, называемое "зерном", подается на вход алгоритма. Затем алгоритм производит серию математических операций для генерации следующего числа в последовательности. И последующие числа генерируются на основе предыдущих чисел в последовательности.
| Преимущества | Недостатки |
|---|---|
| Быстрая генерация случайных чисел | Могут быть предсказуемыми, если известно начальное число (зерно) |
| Простая реализация | Не генерируют истинно случайные числа |
| Возможность воспроизведения последовательности |
Генераторы на основе внешних источников
Генераторы на основе внешних источников получают случайные числа из внешних источников, таких как шум электронных устройств или временные характеристики физических процессов.
Преимуществом таких генераторов является то, что они способны производить более криптографически стойкие случайные числа в сравнении с алгоритмическими генераторами. Однако, они более сложны в реализации и требуют наличия внешнего устройства или физического процесса для получения источника случайности.
| Преимущества | Недостатки |
|---|---|
| Более криптографически стойкие случайные числа | Требуют наличия внешнего источника случайности |
| Сложность воспроизведения последовательности | Более сложная реализация |
Линейные конгруэнтные генераторы
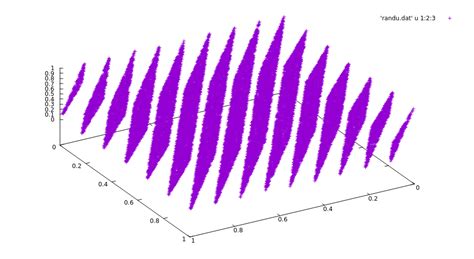
Основная идея линейного конгруэнтного генератора заключается в том, что каждое следующее число в последовательности генерируется путем применения формулы к предыдущему числу. Формула имеет вид:
xn+1 = (a * xn + c) % m
Где:
- xn+1 - следующее число в последовательности генератора
- xn - текущее число в последовательности генератора
- a, c и m - параметры, которые определяются при инициализации генератора
- % - оператор взятия остатка от деления
Параметры a, c и m должны быть выбраны с определенными условиями, чтобы генератор работал правильно. Для некоторых значений параметров генератор может стать периодическим и производить только конечное множество чисел. Для других значений генератор может обладать низкой степенью равномерности распределения.
Важно отметить, что линейные конгруэнтные генераторы являются псевдослучайными, так как последовательность чисел, которую они генерируют, является детерминированной и повторяющейся после определенного числа итераций. Они не могут гарантировать высокую степень случайности, и для некоторых приложений может потребоваться использование более сложных алгоритмов.
Статистические тесты случайности
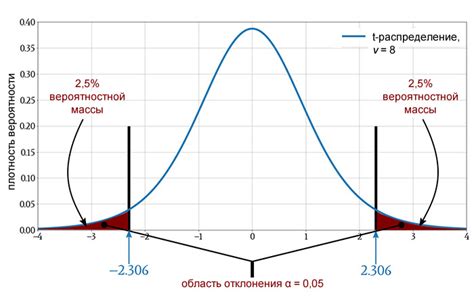
Один из наиболее распространенных статистических тестов - тест хи-квадрат. Он основывается на сравнении фактической и ожидаемой частоты появления различных значений в последовательности случайных чисел. Если различия между ними незначительны, то можно сказать, что генератор работает с высокой степенью случайности.
Еще одним статистическим тестом случайности является тест Колмогорова-Смирнова. Этот тест позволяет проверить, насколько полученная последовательность чисел отличается от равномерного распределения. Если разница незначительна, то можно считать, что генератор создает случайные числа с хорошей степенью качества.
Также существуют и другие статистические тесты случайности, такие как тест серий и тесты на автокорреляцию. Цель всех этих тестов - проверить, насколько полученные случайные числа отвечают определенным критериям случайности.
Важно отметить, что ни один тест не может дать абсолютную гарантию случайности. Однако, применение различных статистических тестов позволяет повысить степень уверенности в случайности полученных чисел и улучшить качество генератора случайных чисел.
Криптографические генераторы случайных чисел

Криптографические генераторы случайных чисел (КГСЧ) представляют собой специальные алгоритмы, которые используются в криптографии для создания случайных чисел, которые должны быть невозможными для предсказания или воспроизведения.
В отличие от обычных генераторов случайных чисел, которые могут быть предсказаны или подвержены определенным паттернам, криптографические генераторы основываются на сложных математических алгоритмах и физических процессах, таких как радиоактивный распад или электромагнитные шумы.
Криптографические генераторы обладают двумя важными свойствами: случайностью и равномерностью распределения чисел. Это означает, что каждое сгенерированное число является результатом полностью случайного процесса и вероятность его появления одинакова для всех чисел в диапазоне.
Такие генераторы не только используются в криптографии для создания случайных ключей, но и в ряде других приложений, где требуется высокая степень непредсказуемости и неповторяемости, например, в розыгрышах и лотереях.
Однако следует отметить, что даже криптографические генераторы случайных чисел могут иметь некоторые ограничения и уязвимости. Поэтому для использования в криптографии рекомендуется выбирать надежные алгоритмы, прошедшие проверку специалистами и подтвержденные соответствующими сертификатами безопасности.
Устройственная случайность

Этот метод основан на предположении, что физические процессы, такие как шумы внутри компьютера или непредсказуемые физические события, способны создавать случайные значения. При использовании подобных устройств и событий можно получить гораздо более случайные числа, чем использование математических алгоритмов
Процесс устройственной случайности включает в себя следующие шаги:
| Шаг | Описание |
| 1 | Сбор случайных данных |
| 2 | Анализ собранных данных |
| 3 | Преобразование данных в случайные числа |
На первом шаге осуществляется сбор случайных данных. Это могут быть, например, данные о температуре процессора, электромагнитные импульсы, шумы радиоэфира или данные о нажатии клавиши на клавиатуре. Чем больше и разнообразнее источников случайных данных, тем более надежными будут полученные случайные числа.
Затем собранные данные проходят анализ, чтобы определить, насколько они случайны. Для этого могут применяться статистические методы, такие как тесты на равномерность и независимость.
На последнем шаге производится преобразование собранных данных в случайные числа. Это может быть достигнуто с помощью математических операций, таких как генерация случайного числа в заданном интервале или подбор случайного бита.
Важно отметить, что методы устройственной случайности не являются абсолютно случайными, поскольку все физические процессы в конечном итоге являются детерминированными. Однако, за счет сложности и непредсказуемости этих процессов, генераторы случайных чисел, основанные на устройственной случайности, позволяют получить числа, которые считаются случайными на практике.
Факторы, влияющие на качество генератора случайных чисел

- Алгоритм генерации
- Сид генератора
- Количественные параметры
- Время инициализации
Алгоритм, используемый в генераторе случайных чисел, должен быть надежным и обеспечивать равномерное распределение чисел. При выборе генератора следует обратить внимание на использование математической основы, такой как алгоритм Мерсенна-Твистера или Xorshift.
Сид (seed) генератора случайных чисел – это начальное значение, которое используется для инициализации генератора. Важно выбрать случайное и уникальное начальное значение, чтобы исключить возможность предугадывания последовательности чисел.
Параметры, связанные с количеством и диапазоном генерируемых чисел, должны быть выбраны с учетом нужд конкретной задачи. Например, для розыгрыша цифровых призов, диапазон чисел может быть от 0 до 9, а количество чисел – равным количеству призов.
Процесс инициализации генератора случайных чисел должен быть достаточно сложным, чтобы предотвратить воспроизводимость последовательности чисел и борьбу со случайностью.
Учитывая эти факторы, можно выбрать генератор случайных чисел, который обеспечит высокое качество и надежность в проведении розыгрышей и других случайных событий.
Применение генераторов случайных чисел в различных областях

- Игровая индустрия: Генераторы случайных чисел используются для создания элементов случайности в играх, таких как кости, карты, лотереи и рулетки. Они обеспечивают справедливость и разнообразие игрового опыта, делая его более интересным и захватывающим.
- Криптография: В криптографии генераторы случайных чисел используются для создания ключей шифрования и других криптографических параметров. Высокое качество случайности генератора является ключевым фактором для обеспечения безопасности в криптографических системах.
- Моделирование и симуляция: В научных и инженерных приложениях генераторы случайных чисел используются для создания стохастических моделей и симуляций. Они позволяют исследовать случайные события и оценивать вероятности различных исходов в различных сценариях.
- Финансовая аналитика: Генераторы случайных чисел используются для моделирования и анализа финансовых рынков. Они помогают оценить риски, прогнозировать цены акций и производить другие финансовые расчеты, учитывающие случайные факторы.
- Тестирование программного обеспечения: Генераторы случайных чисел используются для создания случайных входных данных при тестировании программного обеспечения. Это помогает выявить ошибки и непредсказуемое поведение программы, которые могут возникнуть при различных комбинациях входных данных.
Во всех этих областях использование высококачественных генераторов случайных чисел является важным фактором для достижения надежных и точных результатов. Надеемся, что вы теперь имеете более полное представление о применении генераторов случайных чисел в различных областях.