Модуль – это математическая функция, которая возвращает абсолютное значение числа. Другими словами, модуль приводит число к его положительному значению, игнорируя его знак. Принцип работы модуля может быть использован в различных областях математики, физики и программирования для решения разнообразных задач.
Модуль можно представить в виде выражения |x|, где x – это число. Если x положительное, то модуль равен самому числу: |x| = x. Если же x отрицательное, то модуль равен противоположному значению числа: |x| = -x. Таким образом, модуль всегда возвращает положительное число или ноль.
Принцип работы модуля в уравнениях заключается в том, что значение модуля может использоваться для упрощения и анализа уравнений. Модуль позволяет выделить некоторые особенности уравнений и решить задачу без использования условий или дополнительных действий.
Для решения уравнений с модулем часто используются два подхода. Первый подход заключается в рассмотрении двух случаев: когда выражение внутри модуля положительное и когда оно отрицательное. Таким образом, уравнение разбивается на два уравнения без модуля, которые затем решаются отдельно. Полученные решения объединяются и проверяются на валидность.
Как работает модуль в уравнениях?
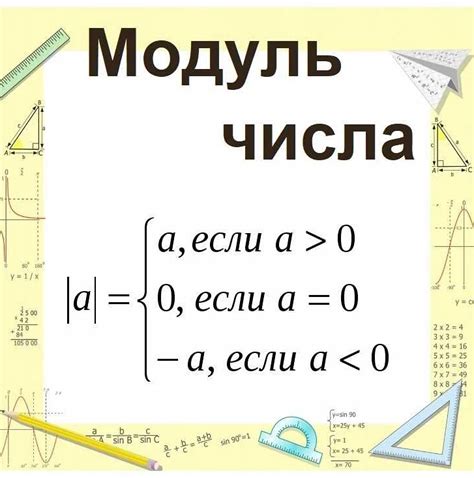
При решении уравнений с модулем необходимо разделить исходное уравнение на две части, в зависимости от знака модуля. Если число внутри модуля положительное или равно нулю, то модуль просто убирается, и мы остаемся с одной частью уравнения. Если число внутри модуля отрицательное, то меняем знак этого числа и решаем уравнение без модуля.
Например, рассмотрим уравнение |x - 3| = 5. Мы можем выполнить два действия, в зависимости от знака модуля. Если x - 3 ≥ 0, то модуль убирается и мы получаем x - 3 = 5. Решая это уравнение, мы найдем одно решение x = 8. Если же x - 3
Таким образом, уравнение |x - 3| = 5 имеет два решения: x = 8 и x = -2.
Модули в уравнениях могут быть использованы для нахождения расстояния между двумя точками на числовой прямой, для определения условий, при которых выражение равно нулю, или для нахождения иных решений, которые удовлетворяют определенным условиям.
Объяснение работы модуля
Для положительных чисел модуль равен самому числу, так как расстояние от положительного числа до нуля равно самому числу. Например, модуль числа 7 равен 7.
Для отрицательных чисел модуль равен числу с обратным знаком, так как расстояние от отрицательного числа до нуля равно расстоянию от числа с обратным знаком до нуля. Например, модуль числа -3 равен 3.
Функция модуля в уравнениях используется для нахождения решений уравнений с абсолютными значениями. При решении таких уравнений необходимо рассмотреть два случая: один для положительного значения под модулем, другой для отрицательного значения под модулем. После решения обоих случаев получаем два возможных значения переменной.
Например, для уравнения |x - 5| = 3 имеем два случая: x - 5 = 3 и x - 5 = -3. Решив каждое из этих уравнений, получаем x = 8 и x = 2. Таким образом, у уравнения |x - 5| = 3 два возможных значения переменной x: 8 и 2.
| Число | Модуль числа |
|---|---|
| 7 | 7 |
| -3 | 3 |
| 0 | 0 |
Решение примеров с использованием модуля
Предположим, у нас есть задача: нужно найти расстояние, которое пройдет тело за определенное время, если ускорение известно. Формула, которую мы можем использовать, выглядит следующим образом: расстояние = ускорение * время.
Рассмотрим пример: тело с постоянным ускорением a = 5 м/c2 движется в течение времени t = -3 секунды. Здесь у нас возникает проблема: время не может быть отрицательным, а расстояние не может быть отрицательным. Для решения этой проблемы мы можем использовать модуль.
| Условие | Решение |
|---|---|
| a = 5 м/c² | |
| t = -3 секунды | |
| Расстояние = |a * t| | |
| Расстояние = |5 * -3| | |
| Расстояние = 15 метров |
Итак, при отрицательном времени мы использовали модуль, чтобы получить положительное значение расстояния. Это позволяет нам получить физически реалистичный ответ на задачу.
Примеры уравнений с модулем
Рассмотрим пример уравнения с модулем:
- Задача: Решить уравнение |2x - 5| = 9.
В данном примере, число внутри модуля равно 2x - 5. Рассмотрим два варианта:
- Когда 2x - 5 >= 0:
- Когда 2x - 5
-(2x - 5) = 9
-2x + 5 = 9
-2x = 4
x = -2
2x - 5 = 9
2x = 14
x = 7
Таким образом, решением уравнения |2x - 5| = 9 являются два числа: x = 7 и x = -2.
В данном примере, число внутри модуля равно x + 3. Рассмотрим два варианта:
- Когда x + 3 >= 0:
- Когда x + 3
-(x + 3) = 6
-x - 3 = 6
-x = 9
x = -9
x + 3 = 6
x = 3
Таким образом, решением уравнения |x + 3| = 6 являются два числа: x = 3 и x = -9.
В данном примере, число внутри модуля равно 2x + 1. Рассмотрим два варианта:
- Когда 2x + 1 >= 0:
- Когда 2x + 1
-(2x + 1) = 4
-2x - 1 = 4
-2x = 5
x = -2.5
2x + 1 = 4
2x = 3
x = 1.5
Таким образом, решением уравнения |2x + 1| = 4 являются два числа: x = 1.5 и x = -2.5.