Математический аналитик – это специалист, который изучает отношения и взаимодействия между математическими объектами и явлениями. Его работа заключается в анализе данных, моделировании и создании математических моделей, которые используются для решения различных проблем и задач. Математический аналитик играет важную роль в науке, экономике, физике, компьютерных науках и других областях, где требуется глубокое понимание чисел и их взаимоотношений.
Основные принципы работы математического аналитика включают сбор и анализ данных, использование статистических методов, построение математических моделей и прогнозов, а также разработку эффективных алгоритмов и методов решения задач. Он также занимается исследованием вероятностей и статистики, анализом стратегий и способов оптимизации, аналитическим моделированием и многими другими задачами.
Основная особенность работы математического аналитика заключается в том, что он решает сложные проблемы, используя математические методы и подходы. Он разрабатывает алгоритмы и модели, которые помогают организациям и предприятиям принимать обоснованные решения, оптимизировать свою деятельность, анализировать риски и прогнозировать будущие события. От математического аналитика требуется владение различными математическими инструментами и знание специализированных программ и пакетов для анализа данных.
Основные принципы работы

- Исследование функций. Математический аналитик проводит детальный анализ функций, изучает их свойства, определяет область определения и область значений, исследует поведение функций на бесконечности.
- Решение уравнений. Математический аналитик занимается решением уравнений различного типа. Он применяет методы алгебры, аналитической геометрии и математического анализа для нахождения корней и выявления свойств уравнений.
- Оптимизация. Важной задачей математического аналитика является оптимизация функций. Он ищет максимумы и минимумы функций, используя методы дифференциального исчисления и численных методов.
- Исследование пределов. Математический аналитик анализирует предельные значения функций при приближении аргументов к определенным значениям. Он определяет пределы функций и изучает их свойства.
- Интегрирование. Математический аналитик занимается нахождением определенных и неопределенных интегралов функций. Он применяет методы интегрирования для нахождения площади под кривыми, вычисления объемов и других задач.
Основные принципы работы математического аналитика позволяют ему исследовать различные математические объекты и применять полученные знания для решения разнообразных задач в науке, технике, экономике и других областях.
Отбор и анализ данных
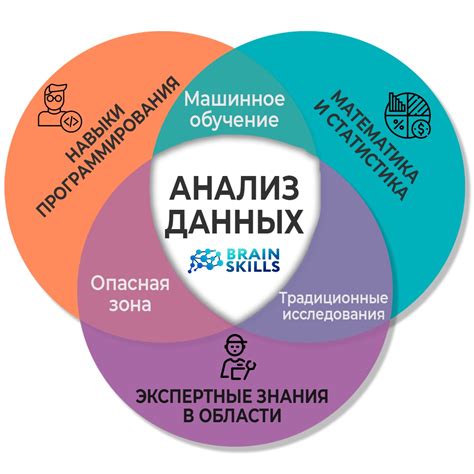
Первый этап - сбор данных. Математический аналитик должен уметь собирать информацию из различных источников, таких как базы данных, веб-страницы, файлы Excel и другие. Важно уметь работать с большими объемами данных и грамотно их структурировать для дальнейшего анализа.
После сбора данных следует их очистка и предобработка. Это включает в себя удаление ошибочных или неполных записей, заполнение пропущенных значений, масштабирование данных и другие манипуляции для устранения шумов и искажений.
Далее проводится анализ данных, включающий статистические методы, машинное обучение, визуализацию и т.д. Математический аналитик использует различные алгоритмы и модели для поиска интересных закономерностей и зависимостей в данных. Он также обращает внимание на выбросы и аномалии, которые могут быть важными факторами в решении реальных задач.
Таким образом, отбор и анализ данных являются важной частью работы математического аналитика. Этот процесс требует навыков работы с различными источниками данных, умения проводить статистический анализ и интерпретировать результаты. Качественный анализ данных помогает принимать осознанные решения и находить ценные закономерности для построения эффективных моделей и стратегий в различных сферах деятельности.
Использование математических моделей

Использование математических моделей позволяет упростить сложные реальные системы и процессы, а также предсказывать их поведение в различных условиях. Модели могут быть применены в различных областях, включая физику, экономику, биологию, информатику и т. д.
Создание математической модели требует учета всех важных факторов и переменных, которые могут влиять на систему или процесс. Важно также выбрать подходящие математические уравнения и методы, которые можно применить для описания системы.
Математические модели могут быть представлены в виде уравнений, графов, таблиц и других форм. Они могут использоваться для анализа, прогнозирования, оптимизации и принятия решений. Математические модели могут быть статическими или динамическими, линейными или нелинейными, дискретными или непрерывными.
Преимущества использования математических моделей включают точность, возможность проведения экспериментов виртуально, анализ различных вариантов и сценариев, экономию времени и ресурсов. Однако, при использовании математических моделей необходимо принимать во внимание их ограничения, такие как приближения и предположения, на которых основана модель.
Использование математических моделей имеет широкий спектр применений, начиная от простых задач до сложных систем. Оно играет важную роль в научных исследованиях, промышленности, финансовой аналитике, медицине и других областях, где необходимо анализировать и прогнозировать поведение системы или процесса.
Разработка алгоритмов
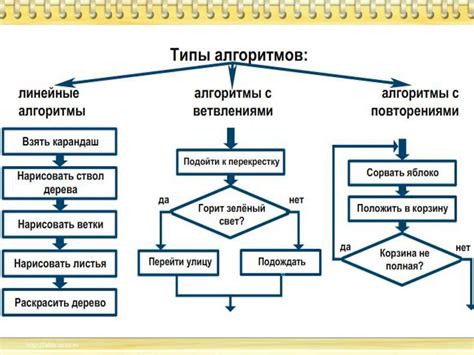
В процессе разработки алгоритма математический аналитик должен учесть все возможные варианты событий и предусмотреть обработку исключительных ситуаций. Алгоритм должен быть эффективным и оптимизированным, чтобы минимизировать время выполнения задачи и использование ресурсов.
Разработка алгоритма включает в себя следующие шаги:
- Анализ проблемы и составление плана действий.
- Определение входных и выходных данных.
- Разработка структуры алгоритма и выбор подходящих методов и операций.
- Реализация алгоритма на выбранном языке программирования.
- Тестирование и отладка алгоритма.
После разработки алгоритма, математический аналитик должен протестировать его на различных входных данных и проверить его корректность и эффективность. При необходимости алгоритм может быть доработан и оптимизирован.
Разработка алгоритмов является неотъемлемой частью работы математического аналитика и требует от него умения абстрагироваться от конкретной задачи, анализировать ее с точки зрения алгоритмической реализации и создавать эффективные и оптимизированные решения.
Визуализация результатов
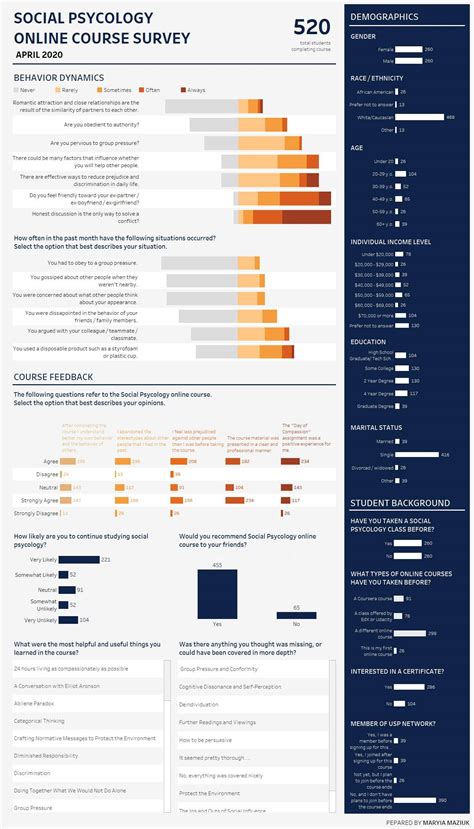
Одним из наиболее распространенных способов визуализации является построение графиков функций. График функции позволяет увидеть зависимость ее значений от значения аргумента. Это помогает выявить особенности функции, такие как экстремумы, точки перегиба, асимптоты и др.
Кроме графиков функций, математический аналитик может использовать и другие способы визуализации, например, построение графиков векторов, поверхностей и множеств точек. Это позволяет исследовать отображение многомерных данных и визуализировать их в пространстве.
Визуализация результатов в математическом анализе может быть осуществлена с использованием специализированных компьютерных программ и инструментов, таких как Matplotlib, Gnuplot, Wolfram Mathematica и др. Эти инструменты позволяют строить графики, рисовать диаграммы, создавать трехмерные модели и применять различные методы визуализации данных.
Особенности профессии математического аналитика

Аналитическое мышление. Одной из ключевых особенностей математического аналитика является его способность мыслить аналитически. Он обладает умением критически оценивать информацию, формулировать и проверять гипотезы, а также принимать обоснованные решения на основе полученных данных.
Математические знания. Наличие глубоких знаний в области математики является основополагающим фактором для математического аналитика. Он должен владеть различными методами вычислений, статистическими методами и моделями, а также быть знакомым с алгоритмами и программированием.
Работа с большими объемами данных. Математический аналитик часто сталкивается с обработкой и анализом больших объемов данных. Он должен быть способен эффективно справляться с такими задачами, используя специализированные программы и алгоритмы для обработки и визуализации данных.
Вероятностный анализ. Важной составляющей работы математического аналитика является вероятностный анализ. Он применяет статистические методы и модели для предсказания и определения вероятности различных событий и исходов. Это позволяет ему принимать взвешенные решения на основе статистических данных.
Все эти особенности в сочетании делают профессию математического аналитика уникальной и требующей специальных навыков и знаний. Эта профессия является востребованной во многих отраслях и может предоставить много перспектив и возможностей для развития карьеры.
Гибкий график работы
Математический аналитик может организовать свой рабочий день так, чтобы загруженность была равномерно распределена и учитывала индивидуальные особенности работника. Это особенно важно для тех, кто предпочитает работать в ночное время или имеет свободный график работы.
Гибкий график работы позволяет математическому аналитику эффективно планировать свои задачи и управлять своим временем. Так, например, можно сделать паузу для перерыва или отдыха, когда это наиболее необходимо, и продолжить работу позднее.
Наличие гибкого графика работы помогает осуществлять более качественный анализ математических данных, так как выполнение сложных задач требует высокой концентрации и внимания. Более того, гибкий график позволяет избежать нервного истощения, связанного с долгим пребыванием на рабочем месте.
Таким образом, гибкий график работы - одно из преимуществ, которыми обладает математический аналитик. Он позволяет оптимизировать работу, учитывая индивидуальные особенности и эффективно управлять своим временем.
Необходимость постоянного обучения

Постоянное обучение позволяет математическому аналитику оставаться на передовой позиции и обеспечивает конкурентные преимущества на рынке труда. Он может изучать новые методы и технологии, применять их в своей работе и достигать более высоких результатов. Также постоянное обучение помогает улучшить навыки решения задач и анализа данных.
Кроме того, математический аналитик должен следить за новыми публикациями и научными исследованиями в своей области. Он должен быть в курсе последних достижений, чтобы применять их в своей работе и находить новые подходы к решению проблем. Необходимость постоянного обучения также связана с появлением новых инструментов и программных продуктов, которые могут значительно улучшить его трудовую деятельность.
Высокий уровень ответственности

У аналитика есть огромная ответственность за правильность собранных данных, анализ и интерпретацию результатов. Математический аналитик должен быть внимателен к деталям и обладать аналитическим мышлением, чтобы изучить сложные математические концепции и методики.
Доверие является важным аспектом работы математического аналитика. Заказчики и коллеги полагаются на его компетентность и точность в своей работе. Небрежность или неосторожность может привести к серьезным ошибкам, которые могут иметь опасные последствия.
Командная работа

Одним из ключевых преимуществ командной работы является возможность обмена идеями и знаниями между участниками. Каждый член команды может внести свой вклад и поделиться своими навыками и опытом, что позволяет решать задачи более эффективно и качественно.
Кроме того, командная работа позволяет распределить работу между участниками, что способствует более эффективному использованию ресурсов и повышению производительности. Каждый член команды может заниматься своей специализированной областью или выполнять определенные задачи, что увеличивает эффективность процесса работы.
Однако командная работа также может привести к определенным сложностям. Важно учитывать индивидуальные особенности и мнения участников команды, чтобы достичь согласия и гармоничного сотрудничества. Коммуникация играет важную роль в командной работе, поэтому важно научиться эффективно общаться и договариваться с другими участниками команды.
Таким образом, командная работа является незаменимым инструментом математического аналитика. Она способствует достижению лучших результатов, эффективному использованию ресурсов и обмену знаниями. Умение работать в команде является важным качеством для математического аналитика и помогает ему успешно справляться с поставленными задачами.
Применение в различных отраслях

- Физика: Математический анализ используется для моделирования и предсказания физических явлений, таких как движение, электромагнетизм и квантовая механика.
- Инженерия: В инженерных расчетах и конструкциях применяются принципы математического анализа для оптимизации процессов, анализа прочности и структурного проектирования.
- Экономика: Математический анализ играет важную роль в экономическом моделировании, оптимизации финансовых портфелей и принятии решений на основе данных.
- Биология: В биологических и медицинских исследованиях математический анализ используется для анализа генетических данных, моделирования популяций и изучения биологических систем.
- Информационные технологии: В области компьютерной науки и искусственного интеллекта математический анализ применяется для разработки алгоритмов, обработки данных и оптимизации производительности систем.
Это лишь небольшой перечень отраслей, в которых применяются принципы и методы математического анализа. Его универсальность и широкое применение делают его одним из ключевых инструментов для понимания и решения сложных проблем в различных областях знаний.