Второй закон Ньютона, также известный как закон аксиомы, является одним из основных принципов классической механики. Он формулирует зависимость между силой, массой и ускорением объекта. Очень часто этот закон применяется в различных науках и инженерных расчетах для определения движения тела.
Движение по окружности является довольно интересным явлением с точки зрения физики. Многие важные приложения этого явления включают механику спутников, молекулярную физику и даже сравнительную анатомию. Успех в понимании движения по окружности часто зависит от умения применять второй закон Ньютона к этой ситуации.
Применение второго закона Ньютона в движении по окружности требует понимания взаимодействия трех основных факторов: силы, массы и ускорения. Второй закон Ньютона формулирует, что сила, действующая на объект, равна произведению его массы на ускорение. В случае движения по окружности, сила, действующая на объект, направлена в место, которое они относятся к центру окружности.
Второй закон Ньютона позволяет нам вывести важную формулу в движении по окружности: сила, необходимая для сохранения объекта на круговой траектории, равна произведению его массы на квадрат скорости деленное на радиус окружности. Эта формула позволяет нам понять, как изменение массы, ускорения или радиуса окружности влияет на необходимую силу для поддержания движения объекта по этой траектории.
Второй закон Ньютона: основные принципы

Математический вид второго закона Ньютона можно записать следующим образом:
F = m*a
где:
- F - сила, действующая на тело;
- m - масса тела;
- a - ускорение тела.
Сила, масса и ускорение являются векторными величинами, поэтому направление силы, массы и ускорения должны быть указаны.
Второй закон Ньютона позволяет рассчитывать силу, действующую на тело, если известны его масса и ускорение. Также, этот закон позволяет определить ускорение тела, если известна сила, действующая на него, и его масса.
Применение второго закона Ньютона особенно полезно при анализе движения тел по окружности. В этом случае, при равномерном движении по окружности, на тело действуют две силы: центростремительная сила и сила трения. Используя второй закон Ньютона, можно определить равномерность или неравномерность движения, а также исследовать зависимость между силой трения и радиусом окружности.
Сила как причина движения

В движении по окружности сила, направленная к центру окружности, называется центростремительной силой. Она является основным фактором, определяющим радиус окружности и скорость движения тела.
Сила как причина движения может быть представлена векторно, указывая не только величину, но и направление действия силы. Векторная сумма всех сил, действующих на тело, называется силой результирующей. Она может изменять скорость и направление движения тела.
Применение второго закона Ньютона и понимание силы как причины движения позволяют анализировать и предсказывать движение тела по окружности, а также оптимизировать параметры движения для достижения заданных целей.
Зависимость ускорения от приложенной силы
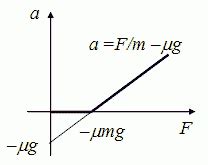
Второй закон Ньютона утверждает, что ускорение тела прямо пропорционально силе, действующей на него, и обратно пропорционально его массе. Математически это выражается формулой:
F = m · a
где F - сила, действующая на тело, m - масса тела и a - ускорение, которое оно получает под действием этой силы.
Таким образом, если масса тела остается постоянной, то ускорение будет пропорционально приложенной силе. Чем больше сила, тем больше будет ускорение, и наоборот. Другими словами, если на тело действует большая сила, оно будет набирать скорость быстрее, чем при действии меньшей силы.
Это принципиальное положение имеет особое значение при рассмотрении движения по окружности. Поскольку центростремительное ускорение - это ускорение направленное к центру окружности, возникающее при движении тела по окружности, оно обеспечивается силой, направленной к центру окружности. Такая сила называется центростремительной силой, и её величина определяется по формуле:
Fc = m · ac
где Fc - центростремительная сила, m - масса тела и ac - центростремительное ускорение.
Таким образом, уравновешивая центростремительную силу силой трения или другими силами, мы можем управлять ускорением тела при движении по окружности.
Применение второго закона Ньютона в движении по окружности

Второй закон Ньютона гласит, что сила, приложенная к телу, равна произведению массы тела на его ускорение.
В движении по окружности объект двигается по кривой траектории, но его скорость будет постоянной, если его ускорение направлено к центру окружности. Проекция ускорения на направление, перпендикулярное радиусу окружности, называется центростремительным ускорением. Центростремительное ускорение может быть вызвано силой, направленной к центру окружности.
Таким образом, в движении по окружности второй закон Ньютона могут записать в виде:
m * a = F_centripetal
Где m - масса тела, a - центростремительное ускорение, F_centripetal - центростремительная сила.
Центростремительная сила может быть представлена как произведение массы тела на квадрат скорости, поделенное на радиус окружности:
F_centripetal = m * v^2 / r
Где v - скорость тела, r - радиус окружности.
Применение второго закона Ньютона в движении по окружности позволяет определить необходимую центростремительную силу для поддержания тела на кривой траектории. Это важно для понимания законов физики, а также для применения в реальных ситуациях, таких, как движение автомобиля по дороге с крутыми поворотами или движение спутников вокруг Земли.
Равномерное движение по окружности
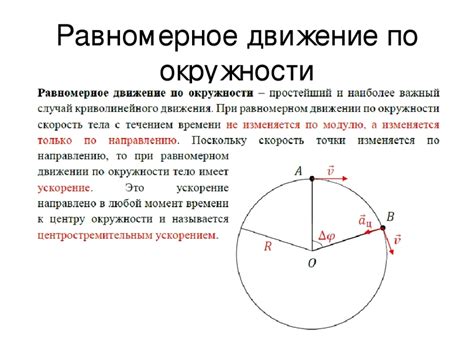
Одним из фундаментальных законов, описывающих движение, является второй закон Ньютона. Согласно этому закону, сила, действующая на тело, равна произведению массы тела на его ускорение. В контексте движения по окружности существуют особенности, связанные с изменением направления ускорения.
Движение по окружности с постоянной скоростью называется равномерным движением, а ускорение в этом случае называют центростремительным ускорением. Центростремительное ускорение направлено всегда к центру окружности и имеет постоянное значение.
Равномерное движение по окружности представляет собой случай равномерного движения с изменением направления движения. Такое движение возможно благодаря непрерывному действию центростремительной силы, обеспечивающей постоянное направление и величину ускорения.
Центростремительное ускорение зависит от радиуса окружности и скорости движения тела по окружности. Ускорение пропорционально квадрату скорости и обратно пропорционально радиусу окружности. Чем больше скорость и меньше радиус, тем больше центростремительное ускорение.
Равномерное движение по окружности широко применяется в различных областях, включая физику, инженерию, аэронавтику и многие другие. Также оно находит свое применение в спорте, например, при велосипедных и автомобильных гонках, где езда по кругу требует понимания основных принципов равномерного движения по окружности.
Неравномерное движение по окружности

Все тела, движущиеся по окружности, совершают некоторое неравномерное движение. Неравномерное движение по окружности характеризуется изменением скорости и ускорения тела в разных точках его траектории.
Второй закон Ньютона позволяет рассчитать ускорение тела, движущегося по окружности. Данный закон формулируется следующим образом:
Ускорение тела, движущегося по окружности, направлено к центру окружности и пропорционально радиусу окружности и квадрату скорости.
Таким образом, чем больше радиус окружности и квадрат скорости, тем больше ускорение. В точках окружности, где радиус максимален, ускорение также достигает своего максимума. В центре окружности ускорение равно нулю, так как радиус равен нулю.
Неравномерное движение по окружности имеет важные практические применения. Например, в автомобильных гонках для поворота транспортного средства необходимо применять специальные приемы, чтобы снизить радиус поворота и увеличить ускорение.
Неравномерное движение по окружности также применяется в промышленности, например, при изготовлении металлических деталей методом термической обработки. Быстрое вращение детали на окружности позволяет равномерно прогреть ее и достичь необходимых свойств.