Линейная функция - это особый тип математического отображения, который представляет собой прямую линию на координатной плоскости. Она имеет формулу y = kx + b, где k и b - постоянные значения, а x и y - переменные, представляющие собой координаты на плоскости. Основные принципы и правила работы с графиком линейной функции позволяют понять его свойства и использовать его для различных расчетов и прогнозирования.
Один из важнейших принципов работы графика линейной функции - это то, что он всегда будет прямой линией. Это означает, что между любыми двумя точками на графике можно провести прямую линию, которая будет являться его частью. Как и другие прямые линии, график линейной функции может иметь положительный или отрицательный наклон, а также быть параллельным одной из осей координат.
График линейной функции также имеет свойства, связанные с значениями постоянных k и b. Наклон прямой линии определяется значением k: если оно положительное, то график будет наклонен вправо, если отрицательное - влево. Значение b определяет сдвиг графика вдоль оси y. Если b положительное, то график будет сдвинут вверх, если отрицательное - вниз. Важно помнить, что при изменении значения k и b график будет менять свою форму и положение, но останется прямой линией.
Определение линейной функции и её графика
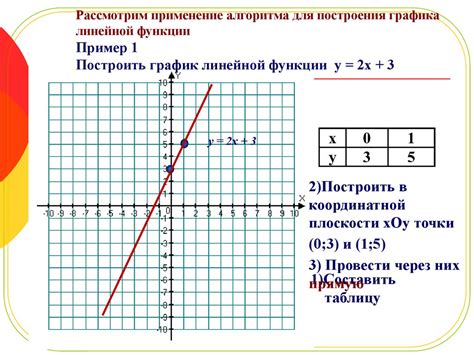
График линейной функции представляет собой множество точек (x, y), где x - значение переменной, а y - соответствующее значение функции. Чтобы нарисовать график, необходимо выбрать несколько значений x, подставить их в уравнение функции и найти соответствующие значения y. Затем эти точки можно отметить на координатной плоскости и соединить прямой линией. Прямая будет проходить через все эти точки и характеризовать свойства линейной функции.
График линейной функции может иметь различные формы. Если значение коэффициента k положительное, то прямая будет наклонена вверх, а если отрицательное - вниз. Если коэффициент k равен нулю, то прямая будет горизонтальной. Если значение b равно нулю, то прямая будет проходить через начало координат.
Линейные функции активно используются в различных областях, таких как физика, экономика, инженерия и др. Они помогают моделировать и анализировать зависимости между различными величинами и предсказывать их значения в разных ситуациях.
| x | y |
|---|---|
| 0 | b |
| 1 | k + b |
| -1 | -k + b |
| 2 | 2k + b |
| -2 | -2k + b |
Линейная функция и её свойства
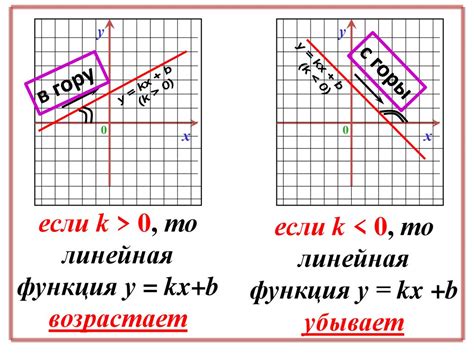
Основные свойства линейной функции:
- График линейной функции всегда является прямой линией. В зависимости от значения коэффициента наклона (k) можно определить её направление: если k > 0, то прямая возрастает, а если k < 0, то прямая убывает.
- Точка на координатной плоскости, через которую проходит прямая линия, называется точкой пересечения с осью ординат (x = 0). Значение этой точки равно свободному члену (b).
- Если значение свободного члена (b) равно нулю, то прямая проходит через начало координат (0, 0). В этом случае линейную функцию можно записать в виде y = kx.
- Если значение коэффициента наклона (k) равно нулю, то график линейной функции будет горизонтальной прямой на уровне свободного члена (b).
Линейные функции являются одной из простейших формул функций и широко применяются в различных областях знаний, начиная от математики и экономики, заканчивая физикой и инженерией. На основе свойств линейной функции можно проводить анализ данных и делать прогнозы.
Прямая линия на координатной плоскости
Прямая линия на координатной плоскости имеет следующие особенности:
- Она соединяет две точки с определенными координатами.
- Прямая линия может иметь положительный или отрицательный наклон.
- Если прямая линия имеет положительный наклон, она стремится к увеличению значений по горизонтальной оси.
- Если прямая линия имеет отрицательный наклон, она стремится к уменьшению значений по горизонтальной оси.
- Каждая точка на прямой линии представляет собой пару значений (x, y), где x - значение по горизонтальной оси, а y - значение по вертикальной оси.
- Прямая линия может иметь нулевой наклон. В этом случае она параллельна горизонтальной оси и представляет уровнение y = k, где k - постоянное значение по вертикальной оси.
График линейной функции может быть полезным инструментом для анализа и представления данных. Он позволяет наглядно показать зависимость между двумя переменными и выявить закономерности.
Координатная плоскость и оси координат
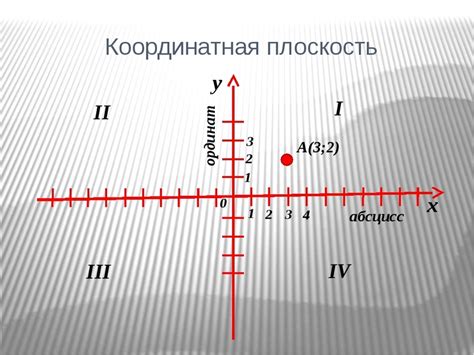
Оси координат разделяют плоскость на четыре квадранта - I, II, III и IV. В квадранте I значения x и y положительные, в квадранте II значения x отрицательные, а y положительные. В квадранте III значения x и y отрицательные, в квадранте IV значения x положительные, а y отрицательные.
Координаты точек на плоскости задаются парой чисел (x, y), где x - это значение по горизонтальной оси, а y - значение по вертикальной оси. Например, точка (2, 3) находится 2 единицы вправо от начала координат по горизонтальной оси и 3 единицы вверх по вертикальной оси.
Оси координат являются важными инструментами для графического представления линейных функций. По оси x откладываются значения аргументов (x), а по оси y - значения функции (y). Затем точки с заданными координатами соединяются прямыми линиями, которые и образуют график линейной функции.
Как построить график линейной функции
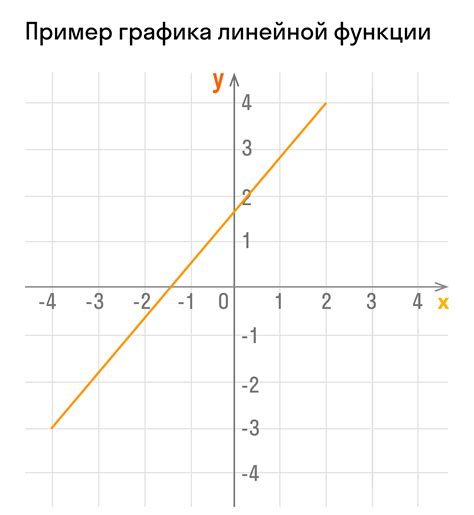
Чтобы построить график линейной функции, необходимо знать её уравнение вида y = kx + b, где k - наклон прямой (коэффициент наклона), b - точка пересечения с осью отсчета OY (смещение функции).
Для начала определите значения аргумента, для которых вы хотите построить график. Затем, используя уравнение функции y = kx + b, вычислите соответствующие значения функции. Эти значения представляют пары (x, y).
После получения всех пар значений (x, y), отметьте их на координатной плоскости. Соедините эти точки линией, чтобы получить график линейной функции.
Не забывайте, что значение кoэффициента наклона k определяет, насколько быстро график функции будет увеличиваться или уменьшаться. Если k < 0, график будет нисходящей прямой, если k > 0, график будет восходящей прямой.
Также, обратите внимание на значение смещения функции b. Если b > 0, график функции будет смещен вверх относительно оси OY, если b < 0, график будет смещен вниз. Если b = 0, график будет пересекать ось OY в точке начала координат.
Имея уравнение линейной функции y = kx + b и понимая влияние её компонентов, вы сможете без труда построить график этой функции на координатной плоскости.
Нахождение точек на графике
Для нахождения точек на графике линейной функции необходимо учесть несколько принципов.
- Зная уравнение линейной функции вида y = kx + b, где k - наклон прямой, а b - свободный член, можно выбирать различные значения x и подставлять их в уравнение для нахождения соответствующих значений y. Найденные значения x и y будут образовывать точки на графике.
- При выборе значений x можно учитывать определенные правила и ограничения. Например, график линейной функции может быть определен только на определенном интервале значений x, что может быть указано в условии задачи.
- Если наклон прямой (k) положительный, то график будет направлен вверх. Если наклон отрицательный, то график будет направлен вниз. Наклон равный нулю будет означать горизонтальную прямую. Если свободный член (b) равен нулю, то график будет проходить через начало координат.
- После нахождения нескольких точек на графике, их можно соединить линиями для визуального представления функции. При этом важно помнить о принципе линейности графика - прямая должна быть гладкой и не иметь отрезков или изломов.
Нахождение точек на графике линейной функции позволяет визуализировать ее поведение и увидеть зависимость между значениями x и y. Этот процесс является важным в анализе данных и применяется в различных областях, таких как экономика, физика, математика и других.
Свойства графика линейной функции
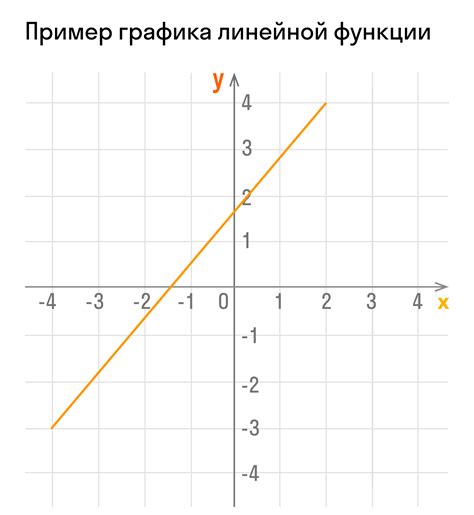
График линейной функции представляет собой прямую линию на плоскости. У данного графика есть несколько свойств, которые определяют его характеристики.
Первое свойство графика линейной функции - прямолинейность. Линейная функция всегда представляет собой прямую линию, которая не имеет изгибов и кривых.
Второе свойство графика - угловой коэффициент. Это число, определяющее наклон прямой. Угловой коэффициент равен отношению изменения значения функции к изменению значения аргумента. Если угловой коэффициент положителен, то график линейной функции будет образовывать угол вправо с положительным направлением оси ординат. Если угловой коэффициент отрицателен, то график будет образовывать угол влево с отрицательным направлением оси ординат.
Третье свойство графика - пересечение с осями координат. График линейной функции всегда пересекает ось ординат в точке с координатами (0, b), где b - это свободный член функции. Если b равно нулю, то график проходит через начало координат (0, 0).
Четвертое свойство графика - монотонность. График линейной функции всегда монотонен, то есть либо возрастает, либо убывает. Возрастающий график имеет положительный угловой коэффициент, а убывающий график - отрицательный угловой коэффициент.
В общем, свойства графика линейной функции позволяют нам легко определить его характеристики и особенности. Эти свойства полезны при анализе и решении задач, связанных с линейными функциями.
Наклон графика
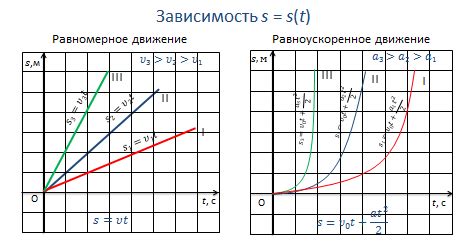
Наклон графика линейной функции можно определить, вычислив разницу между значениями функции на двух точках, лежащих на графике. Если при увеличении аргумента значение функции также увеличивается, то наклон графика называется положительным. Если же значение функции уменьшается при увеличении аргумента, то наклон графика называется отрицательным.
Если наклон графика линейной функции равен нулю, то график является горизонтальной прямой. В этом случае значение функции не меняется при изменении аргумента.
Для определения наклона графика линейной функции можно также использовать коэффициент наклона. Он равен отношению разницы значений функции к разнице аргументов двух точек, лежащих на графике. Если коэффициент наклона положителен, то наклон графика будет положительным, а если коэффициент наклона отрицателен, то наклон будет отрицательным.
| Наклон графика | Тип графика |
|---|---|
| Положительный | График функции возрастает |
| Отрицательный | График функции убывает |
| Ноль | График функции является горизонтальной прямой |
Наклон графика линейной функции важно учитывать при анализе её поведения и применении в практике. Он позволяет определить зависимость между аргументом и значением функции, а также делает возможным прогнозирование и применение функции в различных областях знания.