Проценты – одна из важных тем в учебной программе по математике для учеников 6 класса. Знание процентов не только поможет развить навыки уверенного расчета, но и станет полезным в повседневной жизни. Совладать с этой темой позволит ученикам решать задачи по расчету скидок, наценок и процентов в банковских операциях.
Определение процента, расчет процентной ставки, нахождение процентной доли – эти и другие вопросы будут рассмотрены в данной статье. Мы подготовили простые правила и советы, которые помогут вашему ребенку легко освоить данную тему и достичь успехов в учебе.
Первое правило: при решении задач и расчете процентов важно внимательно читать условие задачи и анализировать его. Нередко условия можно упростить или переформулировать, чтобы задача стала более понятной для ребенка.
Кроме того, важно понимать, как применять полученные знания в реальных ситуациях. Практика – лучший способ запомнить и применять формулы и правила. Подготовка к урокам и решение дополнительных задач помогут вашему ребенку лучше освоить данную тему и повысить успеваемость в школе.
Определение понятия "проценты" и их применение

Процентное значение обычно обозначается символом "%". Например, 50% означает 50 сотых долей или половину от всего.
Проценты часто используются при расчете скидок и налогов, а также в финансовых и экономических вычислениях. Знание процентов позволяет понять, как изменяются величины при процентном росте или убывании.
Для работы с процентами в 6 классе необходимо знать основные формулы и правила решения задач. Важно уметь переводить проценты в десятичную и обратно, а также применять эти знания на практике при решении задач разного уровня сложности.
Основные формулы расчета процентов

- Процент от числа: чтобы найти процент от числа, нужно умножить это число на процент и разделить на 100. Формула выглядит следующим образом: числовое значение * процент / 100.
- Число с процентом: чтобы найти число, которое является определенным процентом от другого числа, нужно число, от которого берется процент, умножить на 100 и разделить на процент. Формула имеет вид: значение процента * 100 / процент.
- Увеличение или уменьшение значения на процент: чтобы увеличить или уменьшить значение на определенный процент, нужно к числу прибавить или вычесть процент от этого числа. Формула для увеличения: числовое значение + процент от значения * числовое значение / 100. Формула для уменьшения: числовое значение - процент от значения * числовое значение / 100.
Знание этих формул позволяет быстро решать задачи на расчет процентов и успешно справляться с математическими заданиями в школе. Рекомендуется практиковаться в решении задач и использовать эти формулы в повседневной жизни, чтобы лучше усвоить материал.
Задачи на проценты с одним неизвестным значением

Для решения подобных задач, важно помнить следующие правила:
- Если нужно найти процент от числа, то формула будет следующей: процентная ставка (в виде десятичной дроби) умножается на число.
- Если известен процент от числа и нужно найти само число, то формула будет обратной: число делится на процентную ставку (в виде десятичной дроби).
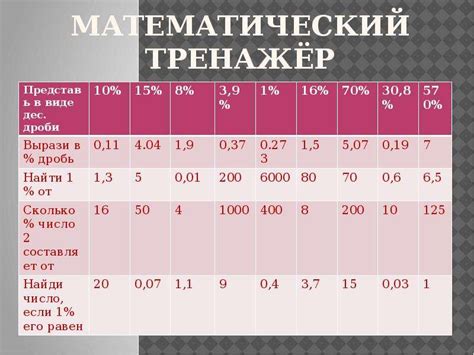
- Используй таблицу процентов для упрощения решения задач. В ней можно найти значения процента от числа для разных процентных ставок (5%, 10%, 15% и т.д.).
Например, решим задачу:
Сколько составляет 20% от числа 80?
Для нахождения 20% от числа 80, нужно воспользоваться формулой: 0,2 (десятая доля) умножить на 80.
| Процент | Число |
|---|---|
| 10% | 8 |
| 20% | 16 |
| 30% | 24 |
| 40% | 32 |
Ответ: 20% от числа 80 составляет 16.
Таким образом, решая задачи на проценты с одним неизвестным значением, необходимо знать формулы для нахождения процента от числа или числа, если известен процент от него, а также использовать таблицу процентов для удобства. Подобные задачи помогут развить навыки работы с процентами и применение математических формул в практических ситуациях.
Задачи на проценты с двумя неизвестными значениями

Решение таких задач основывается на использовании основной формулы процентов:
- Находим первое неизвестное значение, используя формулу процентов: первое значение = второе значение * процент / 100.
- Далее, используя полученное первое значение, находим второе неизвестное значение, также используя формулу процентов: второе значение = первое значение * 100 / процент.
Приведем пример задачи на проценты с двумя неизвестными значениями:
Бабушка купила отличный пылесос со скидкой 20%. Оплатила она его 4000 рублей. Найдите полную цену пылесоса до скидки и размер скидки.
Решение:
- Найдем полную цену пылесоса до скидки, используя формулу: полная цена = оплаченная цена * 100 / (100 - процент).
- Подставляем известные значения: полная цена = 4000 рублей * 100 / (100 - 20) = 4000 * 100 / 80 = 5000 рублей.
- Теперь найдем размер скидки, зная полную цену пылесоса до скидки и оплаченную цену: размер скидки = полная цена - оплаченная цена.
- Подставляем известные значения: размер скидки = 5000 рублей - 4000 рублей = 1000 рублей.
Таким образом, полная цена пылесоса до скидки составляет 5000 рублей, а размер скидки равен 1000 рублей.
Советы для успешной подготовки к решению задач на проценты
- Понимайте концепцию процентов. Прежде чем приступать к решению задач на проценты, важно освоить основные понятия и правила расчета процентов. Необходимо понять, что процент - это доля от целого числа, и научиться применять соответствующие формулы.
- Учите формулы и свойства процентов. Задачи на проценты часто основаны на использовании различных формул и свойств. Постарайтесь заучить основные формулы наизусть, чтобы вам было легче решать задачи. Изучите также свойства процентов, такие как процент от числа, процент изменения и др.
- Разбирайте типичные примеры. Чтение и разбор типичных задач на проценты поможет вам лучше понять, какие шаги нужно предпринять для их решения. Найдите в учебнике или интернете примеры и решите их самостоятельно, обращая внимание на особенности каждого случая.
- Постройте систему упражнений. Для успешной подготовки к решению задач на проценты необходимо много практиковаться. Создайте для себя систему упражнений, состоящую из задач разной сложности. Решайте их регулярно, что поможет вам закрепить материал и развить навыки.
- Обратитесь за помощью. Если у вас возникли сложности с решением задач на проценты, не стесняйтесь обратиться за помощью. Попросите своего учителя или одноклассников объяснить вам неясные моменты. Также можно посмотреть видеоуроки или найти дополнительные материалы в интернете.
- Закрепляйте материал систематически. Чтобы не забыть, что вы изучили, важно регулярно повторять пройденный материал. Проверяйте свои знания, решая тесты или задачи из предыдущих уроков. Это поможет закрепить материал и подготовиться к контрольным работам.