Производная функции в точке Гидк является одним из основных понятий математического анализа. Она позволяет определить скорость изменения функции в данной точке и ее поведение в окрестности этой точки. Производная функции в точке Гидк также позволяет найти угол наклона касательной к графику функции в данной точке.
Формула для вычисления производной функции в точке Гидк имеет вид:
f'(x) = lim(h→0) (f(x+h) - f(x))/h
Где f(x) - исходная функция, x - точка, в которой требуется найти производную, f'(x) - производная функции в точке Гидк.
Производную функции в точке Гидк можно вычислять с помощью различных методов, таких как первые принципы, правила дифференцирования или таблицы производных. Для вычисления производной сложной функции необходимо использовать правило дифференцирования сложной функции.
Для более наглядного представления вычисления производной функции в точке Гидк рассмотрим пример:
Пусть дана функция f(x) = x^2 + 3x - 2. Найдем производную функции в точке Гидк:
f'(x) = lim(h→0) ((x+h)^2 + 3(x+h) - 2 - (x^2 + 3x - 2))/h
Упростим данное выражение и получим:
f'(x) = lim(h→0) (2xh + h^2 + 3h)/h
f'(x) = lim(h→0) 2x + h + 3
Подставим h = 0 и получим:
f'(x) = 2x + 3
Таким образом, производная функции f(x) = x^2 + 3x - 2 в точке Гидк равна 2x + 3.
История производной

Идея производной, одного из важнейших понятий математического анализа, родилась в XVII веке благодаря работам математиков таких как Ньютон и Лейбниц. Они столкнулись с проблемой вычисления скорости изменения функций в определенной точке и для ее решения создали концепцию производной.
Первым, кто использовал идею производной, был античный математик Архимед. В своей работе "Методы" он пытался вычислить площадь криволинейной фигуры путем разбиения ее на большое число прямоугольников. Он применил приближенные значения площадей для каждого прямоугольника и получил значения, которые можно считать производными.
Однако формальное введение понятия производной произошло в XVII веке. Ньютон и Лейбниц независимо друг от друга разработали математическую теорию, в основе которой лежала идея производной. Ньютон разработал метод исчисления поточечных производных, позволяющий находить производные функций в конкретных точках, а Лейбниц ввел символ дифференциала для обозначения производной функции.
Затем исследования в области производных продолжились в XIX и XX веках. Математики углубились в изучение различных классов функций и условий, при которых они имеют производные. Были разработаны методы и алгоритмы для нахождения производной функции в определенной точке.
Сегодня производная функции является одним из важнейших инструментов в математике и науке вообще. Она применяется в различных областях, таких как физика, экономика, статистика и др. Производная позволяет находить максимумы и минимумы функций, определять скорость изменения величин, а также решать различные задачи оптимизации и моделирования.
Определение и основные понятия
Производная функции в точке Гидк обозначается как f'(x0) или dy/dx ∣ x=x0, где f – функция, а x0 – точка, в которой вычисляется производная.
Производная функции в точке показывает, как быстро значение функции изменяется при изменении аргумента x в окрестности точки x0. Если производная положительна, то функция возрастает, если отрицательна – убывает, а если равна нулю – то функция имеет экстремум (максимум или минимум) в точке x0.
Для вычисления производной функции в точке существуют различные правила и формулы, основными из которых являются правила дифференцирования, такие как правило суммы, правило произведения и правило цепной дроби.
Производная функции в точке имеет много практических приложений в различных областях науки и техники, так как позволяет анализировать и оптимизировать различные процессы и функции. Например, производная используется в физике для определения скорости и ускорения тела, в экономике – для определения маржинальной прибыли и затрат, а в компьютерной графике – для создания плавных переходов и анимаций.
Формулы вычисления производной
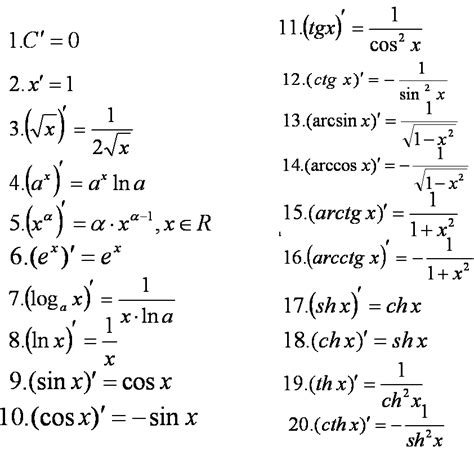
Существует несколько основных формул для вычисления производной функции в точке Гидк. Они основаны на определении производной как предела отношения приращения функции к приращению аргумента, когда последнее стремится к нулю.
Одна из самых простых формул для вычисления производной функции f(x) в точке x = Гидк выглядит следующим образом:
Эта формула является идеализированной, так как строгое определение производной требует существования предела при любом приращении аргумента. Однако, с помощью этой формулы можно приближённо вычислить производную функции в окрестности точки Гидк.
Ещё одна распространённая формула вычисления производной функции в точке Гидк основана на правиле дифференцирования сложной функции:
где g(x) - это функция, производная которой готова или легко вычисляется, а f(x) - сама исходная функция.
Также существуют различные формулы дифференцирования элементарных функций, таких как линейная функция, степенная функция, тригонометрические функции и экспоненциальная функция. Они позволяют вычислить производную этих функций в любой точке Гидк, а также находить производные их линейных комбинаций и композиций.
Использование формул вычисления производной позволяет решать различные задачи, связанные с оптимизацией, анализом функций и построением графиков.
Примеры вычисления производной

Ниже приведены несколько примеров вычисления производной функции в точке Гидк с использованием основных правил дифференцирования:
Пример 1: Вычислить производную функции f(x) = x^2 в точке x = 3.
Решение: Используем правило дифференцирования степенной функции: (x^n)' = n*x^(n-1). Производная функции f(x) = x^2 равна f'(x) = 2*x. Подставляя x = 3, получаем f'(3) = 2*3 = 6.
Пример 2: Вычислить производную функции g(x) = 3*x^4 в точке x = -1.
Решение: Снова используем правило дифференцирования степенной функции. Производная функции g(x) = 3*x^4 равна g'(x) = 12*x^3. Подставляя x = -1, получаем g'(-1) = 12*(-1)^3 = -12.
Пример 3: Вычислить производную функции h(x) = e^x в точке x = 2.
Решение: Используем правило дифференцирования экспоненты: производная функции h(x) = e^x равна h'(x) = e^x. Подставляя x = 2, получаем h'(2) = e^2.
Это лишь несколько примеров вычисления производной функции в точке Гидк. В общем случае, для вычисления производной функции в точке необходимо знание правил дифференцирования и умение их применять с учетом конкретной функции.