Гармоническое колебание - одно из фундаментальных понятий в физике и математике. Это движение, описываемое функцией синуса или косинуса, и имеющее ряд важных свойств. Производная гармонического колебания - одно из таких свойств, играющих важную роль в анализе и моделировании этого явления.
Производная функции представляет собой мгновенную скорость изменения этой функции. В случае гармонического колебания, производная позволяет нам определить, как быстро меняется амплитуда и фаза колебания в каждый момент времени. Это позволяет нам получить информацию о динамике и энергетической потери системы в процессе колебания.
Производная гармонического колебания может быть выражена аналитически с помощью исчисления дифференциального и интегрального исчисления. Ее значение зависит от вида колебания и может быть как положительным, так и отрицательным. Эти значения связаны с направлением движения и интенсивностью колебания. Производная также дает нам информацию о фазовом сдвиге и периоде гармонического колебания.
Основы гармонического колебания
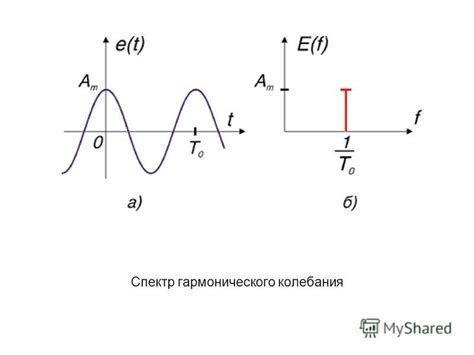
Ключевой характеристикой гармонического колебания является его частота, которая определяет количество полных колебаний, происходящих за единицу времени. Частота колебания обратно пропорциональна его периоду - времени, за которое происходит одно полное колебание.
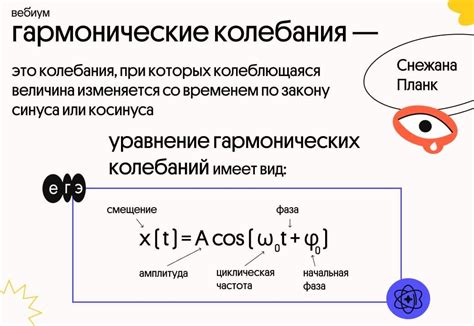
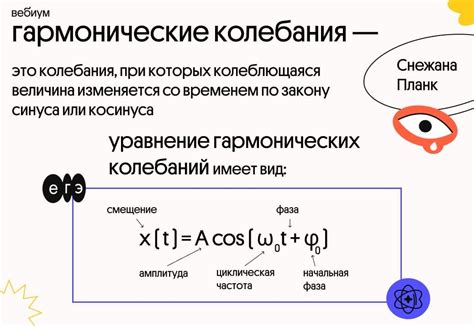
Гармоническое колебание можно представить с помощью математической функции синуса или косинуса. Такое представление позволяет легко определить различные параметры колебания, такие как амплитуда, фаза и начальное смещение.
Амплитуда гармонического колебания - это максимальное отклонение тела от его равновесного положения. Она является мерой энергии колебания и влияет на его интенсивность.
Фаза колебания указывает на текущую стадию колебания в отношении своего начального положения. Она определяется углом отклонения колеблющейся системы от начального положения в определенный момент времени.
Начальное смещение гармонического колебания указывает на его положение в начальный момент времени. Оно определяет, насколько далеко тело отклонилось от своего равновесного положения в начальный момент времени.
Гармоническое колебание является важным явлением в многих областях науки и техники, и его изучение дает нам возможность понять и описать различные процессы, такие как механические вибрации, электромагнитные колебания и звуковые волны.
Что такое гармоническое колебание?

Гармоническое колебание может быть представлено в виде синусоидальной функции, где изменение величины происходит с постоянной частотой и амплитудой. Оно может возникать в различных системах, таких как механические системы, электрические цепи и звуковые волны.
В гармоническом колебании существуют основные понятия, такие как период, частота и амплитуда. Период - это время, за которое колебание повторяется, а частота - количество колебаний в единицу времени. Амплитуда определяет максимальное отклонение от равновесной позиции.
Производная гармонического колебания играет важную роль в его анализе и моделировании. Она позволяет определить скорость изменения величины колебания в каждый момент времени и представить колебание в виде уравнения.
Гармоническое колебание имеет широкий спектр применений, от физических и инженерных наук до биологии и экономики. Оно позволяет описать и объяснить множество явлений и процессов, исследуемых в различных областях науки.
Свойства гармонического колебания
Существуют несколько основных свойств гармонического колебания:
- Периодичность: Гармоническое колебание повторяется через определенное время, называемое периодом. Это означает, что функция, описывающая гармоническое колебание, имеет повторяющуюся структуру.
- Фаза: Фаза гармонического колебания определяет положение начального момента времени для данной точки колебания. Фаза может быть измерена в угловых или временных единицах.
- Амплитуда: Амплитуда гармонического колебания отражает наибольшее значение колебаний и является максимальным удалением от положения равновесия. Чем больше амплитуда, тем более выраженны колебания.
- Фазовая скорость: Фазовая скорость гармонического колебания определяет скорость перемещения волны от одной точки к другой в пространстве. Фазовая скорость зависит от частоты и длины волны колебания.
- Период колебания: Период колебания - это время, за которое происходит одно полное колебание. Он обратно пропорционален частоте колебания и может быть измерен в единицах времени.
- Частота: Частота колебания определяет количество полных колебаний, которые происходят в единицу времени. Она выражается в герцах (Гц) и является обратным значением периода колебания.
Производная исчисления

Производная функции определяется как предел отношения функции к нулю, если аргумент функции стремится к нулю. Определение производной функции включает предел приращения функции и предел изменения аргумента функции, обрабатывающей колебания. Производная используется для вычисления скорости изменения функции в каждой точке и может использоваться для определения экстремальных значений функции. Она также позволяет найти уравнение касательной к графику функции в точке.
Производная гармонического колебания является одним из простейших примеров производной. Гармоническое колебание описывается синусоидальной функцией, где производная в каждой точке равна производной синуса функции. Производная синуса функции определена как косинус функции. Таким образом, производная гармонического колебания является косинусоидальной функцией, которая представляет скорость изменения амплитуды колебания в каждый момент времени.
Исчисление производных имеет множество приложений в физике, инженерии, экономике и других науках. Производные используются для моделирования и анализа различных явлений и процессов, включая движение тел, электрические цепи, финансовые рынки и т.д. Они также играют важную роль в оптимизации и оценке функций, что позволяет находить максимумы и минимумы функций и решать оптимизационные задачи.
Использование производных в исчислении не только позволяет анализировать функции, но и упрощает процесс нахождения экстремумов функций и решения оптимизационных задач. Поэтому, понимание производной и исчисления является важным навыком для математиков, физиков и инженеров, которые занимаются научными и техническими расчетами.
Определение производной

Формально, производная функции в точке определяется как предел отношения изменения значения функции к изменению ее аргумента, приближая точку аргумента к исследуемой. Производная функции обозначается символом "f'(x)" или "df(x)/dx".
Если значение производной положительно, то функция возрастает в данной точке, если отрицательно, то функция убывает. Если производная равна нулю, то функция имеет экстремум в данной точке.
Производная функции описывает мгновенную скорость изменения функции в каждой точке и позволяет изучать графики функций, находить точки наибольшего и наименьшего значения функции, а также определять, является ли функция монотонной, выпуклой или вогнутой.
Правила дифференцирования

В исчислении дифференциалов существуют основные правила, которые позволяют находить производные функций. Для гармонического колебания, эти правила также применяются.
1. Правило линейности: производная суммы функций равна сумме производных каждой из функций. То есть, если имеем функции f(x) и g(x), их сумма h(x) = f(x) + g(x), то h'(x) = f'(x) + g'(x).
2. Правило произведения: производная произведения двух функций f(x) и g(x) равна сумме произведений производной первой функции f'(x) на вторую функцию g(x) и первой функции f(x) на производную второй функции g'(x). То есть, если имеем функции f(x) и g(x), их произведение h(x) = f(x) * g(x), то h'(x) = f'(x) * g(x) + f(x) * g'(x).
3. Правило частного: производная отношения двух функций f(x) и g(x) равна разности произведения производной первой функции f'(x) на вторую функцию g(x) и первой функции f(x) на производную второй функции g'(x), деленной на квадрат второй функции g(x). То есть, если имеем функции f(x) и g(x), их отношение h(x) = f(x) / g(x), то h'(x) = (f'(x) * g(x) - f(x) * g'(x)) / (g(x)^2).
4. Правило дифференцирования обратной функции: если имеем функцию f(x), и она имеет обратную функцию g(x), то производная обратной функции равна единице, деленной на производную исходной функции в точке x. То есть, если есть f(g(x)) = x, то g'(x) = 1 / f'(g(x)).
5. Правило дифференцирования композиции функций: если имеем функции f(x) и g(x), и их композиция h(x) = f(g(x)), то производная композиции равна произведению производной первой функции f'(g(x)) на производную второй функции g'(x). То есть, h'(x) = f'(g(x)) * g'(x).
Эти правила позволяют проводить дифференцирование гармонических колебаний и находить производные в более сложных случаях. Для более глубокого понимания и применения этих правил рекомендуется изучение математического анализа и исчисления.
Принципы дифференциации гармонического колебания
Существуют несколько принципов дифференциации гармонического колебания:
1. Принцип линейности. Для гармонического колебания справедливо свойство линейности: производная гармонической функции также является гармонической функцией с той же частотой, но смещенной фазой и измененной амплитудой. Это означает, что дифференцирование гармонического колебания не меняет его основных характеристик.
2. Принцип суперпозиции. Дифференцирование гармонического колебания может быть выполнено для каждой гармонической компоненты отдельно, а затем результаты сложены по принципу суперпозиции. Это позволяет разбить сложное колебание на более простые компоненты и анализировать их отдельно.
3. Закон сохранения энергии. При дифференциации гармонического колебания играет важную роль закон сохранения энергии. Производная колебания дает информацию об изменении его кинетической и потенциальной энергии в течение времени. Это позволяет оценить эффективность преобразования энергии и рассчитать среднюю мощность колебательной системы.