Производная и функция - основные понятия математического анализа, которые широко применяются в различных областях науки и техники. Производная является одним из основных показателей изменения функции, а функция, в свою очередь, представляет собой правило, сопоставляющее каждому элементу из одного множества одно или несколько значений из другого множества.
Функция - это математический объект, который играет важную роль в моделировании и представлении различных явлений в естественных и социальных науках. Она определяется алгоритмически или при помощи математического выражения, которое позволяет вычислить значение функции для любого входного аргумента. Функции могут быть заданы явно или неявно, а их графики представляют собой кривые в двумерном или пространстве.
Производная - это основной инструмент дифференциального исчисления, который позволяет изучить скорость изменения функции в каждой точке её области определения. Она определяется как предел отношения приращения функции к приращению аргумента при стремлении величины приращения аргумента к нулю. Производная может быть положительной, отрицательной или равной нулю в зависимости от формы графика функции.
Определение и свойства функции
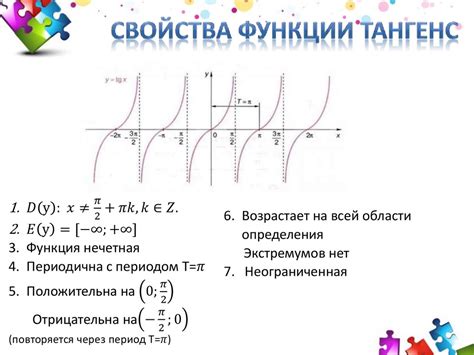
Существуют различные свойства функций:
| Свойство | Описание |
| Определенность | Функция должна быть определена для каждого элемента множества x. Не должно быть ни одного элемента, для которого функция не определена. |
| Единственность значения | Каждому элементу множества x должно соответствовать единственное значение y. Не должно быть двух различных элементов, для которых функция принимает одно и то же значение. |
| Необходимость задания области значений | Область значений функции - это множество всех возможных значений y. Для полного определения функции необходимо указать ее область значений. |
| Зависимость от аргумента | Значение функции зависит от значения аргумента. Изменение аргумента приводит к изменению значения функции. |
| Обратимость | Если каждому элементу множества x соответствует единственное значение y, то функция является обратимой. То есть, существует функция, обратная исходной, которая каждому элементу y ставит в соответствие элемент множества x. |
Понимание определения и свойств функции является важным для изучения производной и ее свойств. Зная, что функция должна быть определена и иметь единственное значение для каждого элемента множества x, мы можем более глубоко изучать производную и ее связь с функцией.
Основы производной и ее назначение

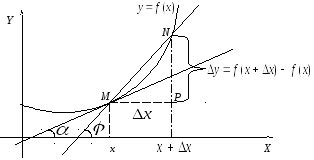
Производная функции f(x) обозначается как f'(x) или dy/dx и определяется как предел отношения изменения значения функции к изменению ее аргумента при стремлении изменения аргумента к нулю:
f'(x) = lim (Δx→0) (f(x + Δx) - f(x))/Δx
Производная может быть интерпретирована геометрически как угловой коэффициент касательной к графику функции в данной точке. Она позволяет определить, является ли функция возрастающей или убывающей, а также найти точки экстремума функции.
Производная имеет множество приложений в различных областях науки и техники. Например, она позволяет определить скорость и ускорение объекта в физике, решать задачи оптимизации в экономике, управлять динамическими системами в инженерии, исследовать процессы в биологии и т. д.
Определение производной может быть выполнено различными методами, такими как геометрический метод, метод конечных разностей, метод дифференцирования элементарных функций и другие. Эти методы позволяют найти производную для широкого класса функций и выразить ее в аналитической форме.
Физическая интерпретация производной
В физике, производная функции может описывать скорость, ускорение или изменение других физических параметров в зависимости от времени. Например, производная пути по времени может дать нам скорость движения тела, а производная скорости по времени - ускорение.
В экономике, производная функции может интерпретироваться как маржинальные издержки или доходы. Например, производная функции общих издержек по производству может показать, как изменяются издержки при изменении объема производства.
В математике производная функции имеет свою собственную интерпретацию. Она показывает скорость изменения наклона касательной линии к графику функции в каждой её точке. Таким образом, производная функции позволяет нам определить, насколько быстро меняется значение функции при малых изменениях её аргумента.
Итак, производная функции имеет широкий диапазон физических интерпретаций. Она позволяет нам понять какие-либо изменения или связь между переменными в задачах из разных областей науки и инженерии.
Геометрическое понятие производной
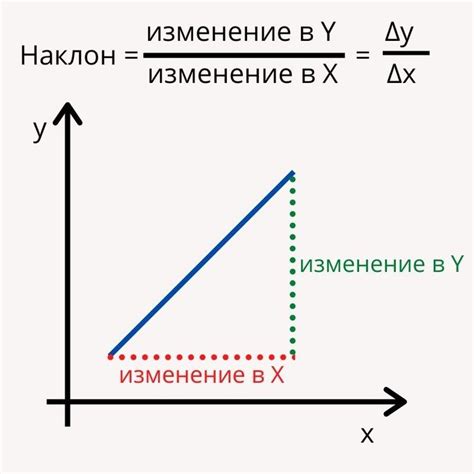
Геометрический смысл производной можно представить с помощью касательной линии к графику функции в заданной точке. Касательная линия касается графика функции только в одной точке и имеет такое же направление скорости изменения функции в этой точке.
Если функция возрастает, то касательная линия будет наклонена вверх, если функция убывает, то касательная линия будет наклонена вниз, а если функция имеет минимум или максимум в данной точке, то касательная линия будет горизонтальной.
| Изменение функции | Касательная линия |
| Функция возрастает |  |
| Функция убывает |  |
| Функция имеет минимум или максимум |  |
Производная функции в данной точке является коэффициентом наклона касательной линии. Чем больше модуль производной, тем круче наклон касательной линии и тем быстрее меняется функция в данной точке.
Определение производной позволяет решать множество задач из различных областей, таких как физика, экономика, статистика и т.д. Благодаря геометрическому понятию производной можно лучше понять поведение функции и применить это знание для решения практических задач.
Методы определения производной: аналитический и графический

Аналитический метод определения производной основан на применении математических формул и правил. При этом используются алгебраические операции и дифференциальное исчисление. Аналитическое определение производной позволяет точно вычислить значение производной в каждой точке функции.
Графический метод определения производной базируется на анализе графика функции. Здесь используется метод касательной, при котором строится касательная к графику в заданной точке. Затем производная определяется как коэффициент наклона касательной.
Оба метода имеют свои преимущества и недостатки и часто применяются в сочетании друг с другом. Аналитический метод позволяет получить точное значение производной и провести математические выкладки, в то время как графический метод дает наглядное представление о поведении функции на графике.
Выбор метода определения производной зависит от конкретной задачи и индивидуальных предпочтений математика. Умение работать с обоими методами позволяет более полно и глубоко исследовать функцию и ее свойства.
Практическое применение производной

Одним из основных применений производной является нахождение экстремумов функции. Используя производную функции, можно определить точки, в которых функция достигает максимального или минимального значения. Это очень полезно, например, при оптимизации процессов в производстве или при поиске максимальной прибыли в экономической деятельности.
Производная также может быть использована для анализа скорости изменения функции. Например, в физике производная используется для определения мгновенной скорости тела в данной точке. Также производная может показать нам, есть ли у функции увеличение или уменьшение в данной точке.
Другое практическое применение производной связано с построением графиков функций. Зная значение производной в каждой точке, мы можем определить поведение функции и построить ее график. Это особенно важно в математике, физике и экономике.
В общем, производная функции является неотъемлемой частью математики и науки в целом. Ее практическое применение позволяет решать множество задач и анализировать различные процессы. Понимание производной позволяет нам получить глубокое представление о функции и способностях математического анализа.