Производные сумм и разностей функций являются одним из основных инструментов дифференциального исчисления. Они позволяют находить производные функций, образованных путем сложения или вычитания других функций. Это важное знание в математике, которое находит свое применение в физике, экономике, статистике и других областях науки и техники.
Методы нахождения производных сумм и разностей функций основаны на применении правила дифференцирования для элементарных функций. Если заданы функции f(x) и g(x), то производная их суммы обозначается как (f + g)'(x) и находится по формуле (f + g)'(x) = f'(x) + g'(x). То есть, производная суммы функций равна сумме их производных.
Аналогично, производная разности функций обозначается как (f - g)'(x) и находится по формуле (f - g)'(x) = f'(x) - g'(x). Таким образом, производная разности функций равна разности их производных.
Для более сложных случаев, когда функции представлены в виде сложных выражений или рациональных функций, используются правила дифференцирования сложных функций и правила дифференцирования частного. Эти правила позволяют находить производные функций, составленных из элементарных функций с использованием операций сложения, вычитания, умножения и деления.
Далее приведены примеры нахождения производных суммы и разности функций для различных типов функций. Решение этих примеров поможет закрепить полученные знания и научиться применять правила дифференцирования на практике.
Определение производной суммы функций
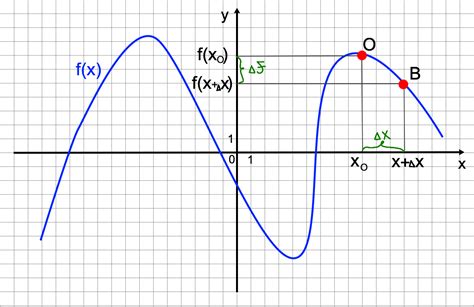
Для определения производной суммы функций необходимо применить правило суммы производных. Согласно этому правилу, производная суммы функций равна сумме их производных.
Формула для определения производной суммы функций выглядит следующим образом:
(f + g)' = f' + g'
где f и g – функции, f' и g' – их производные.
Для нахождения производной суммы функций необходимо найти производные каждой функции по отдельности и затем сложить их.
Рассмотрим пример:
Даны функции f(x) = 3x^2 - 2x + 1 и g(x) = 5x + 2. Найдем производную их суммы.
Сначала найдем производные каждой функции:
f'(x) = 6x - 2
g'(x) = 5
Затем сложим производные:
(f + g)' = f' + g'
(f + g)' = (6x - 2) + 5
(f + g)' = 6x + 3
Таким образом, производная суммы функций f(x) и g(x) равна 6x + 3.
Использование правила суммы производных позволяет упростить процесс нахождения производной суммы функций и сделать его более удобным.
Методы нахождения производной суммы функций
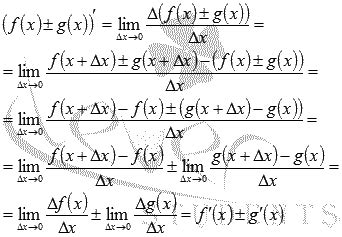
Один из таких методов - метод линейных приближений. Он основан на следующем правиле: производная суммы функций равна сумме производных этих функций. То есть, если имеется функция f(x) и функция g(x), их сумма будет равна h(x) = f(x) + g(x). Тогда производная суммы будет равна h'(x) = f'(x) + g'(x).
Другой метод - метод разделения переменных. В этом случае, если имеются функции f(x) и g(x), их сумма будет равна h(x) = f(x) + g(x). Производная суммы в этом случае будет равна h'(x) = f'(x) + g'(x), то есть производная каждой функции суммируется.
Также существует метод дифференцирования по определению. Он заключается в применении определения производной и нахождении предела отношения приращения функции к приращению аргумента. В случае с суммой функций, производная будет равна пределу отношения приращения суммы функций к приращению аргумента, который можно разложить на сумму пределов отношений приращений функций к приращению аргумента.
Таким образом, нахождение производной суммы функций может быть осуществлено с помощью различных методов, в зависимости от ситуации и характеристик функций. Основные методы включают линейные приближения, разделение переменных и дифференцирование по определению.
Практические примеры нахождения производной суммы функций
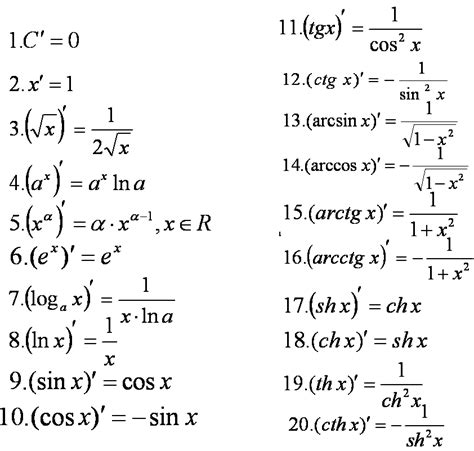
- Пример 1: Найдем производную суммы функций f(x) = 3x^2 + 2x + 1 и g(x) = 2x^3 + 4x:
Сначала найдем производные каждой функции по отдельности:
- f'(x) = 6x + 2
- g'(x) = 6x^2 + 4
Затем сложим производные для получения производной суммы функций:
- (f + g)'(x) = f'(x) + g'(x) = (6x + 2) + (6x^2 + 4) = 6x^2 + 6x + 6
Используя формулы производных элементарных функций, получим:
- f'(x) = cos(x)
- g'(x) = -sin(x)
Сложим производные:
- (f + g)'(x) = f'(x) + g'(x) = cos(x) - sin(x)
Производная экспоненциальной функции равна самой функции, а производная логарифмической функции равна 1/x:
- f'(x) = e^x
- g'(x) = 1/x
Сложим производные:
- (f + g)'(x) = f'(x) + g'(x) = e^x + 1/x
Вышеуказанные примеры показывают, что процесс нахождения производной суммы функций сводится к сложению их производных. Знание этого метода позволяет более удобно и эффективно решать задачи дифференциального исчисления.
Определение производной разности функций
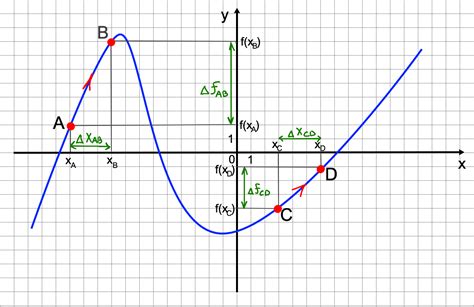
Формула для определения производной разности функций имеет вид:
| Функция | Производная |
|---|---|
| f(x) | f'(x) |
| g(x) | g'(x) |
Производная разности функций вычисляется покомпонентно путем нахождения разности производных отдельных функций.
Пример задачи на нахождение производной разности функций:
Дано две функции f(x) = x^2 и g(x) = 3x.
Найдем производную для функции h(x) = f(x) - g(x).
Сначала найдем производную для функции f(x):
f'(x) = 2x.
Затем найдем производную для функции g(x):
g'(x) = 3.
Теперь вычислим производную разности функций:
h'(x) = f'(x) - g'(x) = 2x - 3.
Таким образом, производная для функции h(x) = f(x) - g(x) равна 2x - 3.
Производная разности функций позволяет упростить задачи на нахождение производных сложных функций и является важным инструментом в математическом анализе.
Методы нахождения производной разности функций
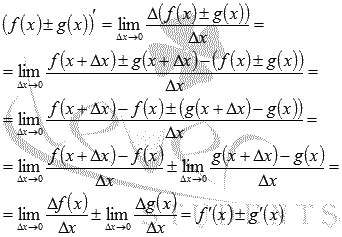
Для нахождения производной разности функций можно использовать несколько методов:
- Метод дифференцирования частных производных.
- Метод дифференцирования с помощью правила Лейбница.
- Метод дифференцирования с помощью правила константы.
Первый метод основан на применении формулы дифференцирования частного производных. При этом сначала производят дифференцирование каждой функции отдельно, а затем вычисляют разность полученных производных.
Второй метод основан на использовании правила Лейбница, которое позволяет дифференцировать произведение двух функций. В этом случае производная разности функций вычисляется по формуле производной первой функции умноженной на вторую функцию, вычтенной произведение первой функции умноженной на производную второй функции.
Третий метод основан на правиле константы, которое утверждает, что производная постоянного множителя равна нулю. Это позволяет произвести дифференцирование каждой функции отдельно, а затем просто вычесть полученные производные.
В зависимости от конкретной функции и условий задачи следует выбирать наиболее удобный метод для нахождения производной разности функций.
Практические примеры нахождения производной разности функций

Производная разности функций может быть полезна в решении различных задач, связанных с изменением значений и скоростями изменения функций. Рассмотрим несколько практических примеров нахождения производной разности функций.
Пример 1:
Пусть имеется две функции, заданные следующим образом:
$$f(x) = 3x^2 + 2x$$
$$g(x) = 2x^3 + 4x^2$$
Найдем производную их разности:
$$f'(x) = (3x^2 + 2x)' = 6x + 2$$
$$g'(x) = (2x^3 + 4x^2)' = 6x^2 + 8x$$
Теперь найдем производную разности:
$$h'(x) = (f(x) - g(x))' = (3x^2 + 2x - (2x^3 + 4x^2))'$$
$$h'(x) = (3x^2 + 2x - 2x^3 - 4x^2)'$$
$$h'(x) = (3x^2 - 4x^2 + 2x - 2x^3)'$$
$$h'(x) = (x^2 - 2x^3 + 2x)'$$
$$h'(x) = 2x - 6x^2 + 2$$
Пример 2:
Рассмотрим две функции:
$$f(x) = 5x^3 + 2x^2 - 3x$$
$$g(x) = 2x^3 + 4x$$
Найдем производную их разности:
$$f'(x) = (5x^3 + 2x^2 - 3x)' = 15x^2 + 4x - 3$$
$$g'(x) = (2x^3 + 4x)' = 6x^2 + 4$$
Теперь найдем производную разности:
$$h'(x) = (f(x) - g(x))' = (5x^3 + 2x^2 - 3x - (2x^3 + 4x))'$$
$$h'(x) = (5x^3 + 2x^2 - 3x - 2x^3 - 4x)'$$
$$h'(x) = (5x^3 - 2x^3 + 2x^2 - 3x - 4x)'$$
$$h'(x) = (3x^3 + 2x^2 - 7x)'$$
$$h'(x) = 9x^2 + 4x - 7$$
Это лишь некоторые примеры нахождения производной разности функций. Подобные вычисления могут быть полезными при анализе изменения значений функций и для нахождения скоростей изменения в различных задачах.
Подводя итоги: методы и примеры нахождения производной суммы и разности функций
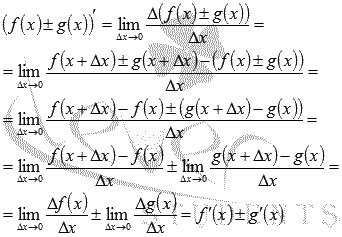
Первым методом является применение обычных правил дифференцирования: если у нас есть две функции, скажем f(x) и g(x), их сумма f(x) + g(x) или разность f(x) - g(x), то производная такой суммы или разности равна сумме или разности производных собственных функций. То есть:
| Функция | Производная |
|---|---|
| f(x) + g(x) | f'(x) + g'(x) |
| f(x) - g(x) | f'(x) - g'(x) |
Данный метод является достаточно простым и позволяет нам находить производные суммы и разности функций без особых проблем.
Приведем пример для лучшего понимания. Пусть у нас есть две функции: f(x) = x^2 + 3x и g(x) = 2x + 5. Необходимо найти производную суммы и разности этих функций.
Производная суммы этих функций будет равна:
(x^2 + 3x)' + (2x + 5)' = (2x + 3) + 2 = 2x + 5
А производная разности функций будет равна:
(x^2 + 3x)' - (2x + 5)' = (2x + 3) - 2 = 2x + 1
Таким образом, мы получили производные суммы и разности данных функций.
Использование данных методов позволяет легко и быстро находить производные суммы и разности функций.