Производные и дифференциалы – это ключевые понятия математического анализа, которые позволяют нам описывать изменения величин и их законы в математической форме. Производная уравнения движения является одним из примеров применения этих понятий в физике. С помощью производной мы можем определить скорость, ускорение и другие величины, связанные с движением тела.
Производная уравнения движения определяется как скорость изменения позиции тела в зависимости от времени. Математически производная выражается через предел отношения приращения позиции ко времени при его бесконечном приближении к нулю. Таким образом, мы получаем функцию, которая описывает изменение скорости тела в зависимости от времени.
Примером уравнения движения, для которого можно найти производную, является движение с постоянной скоростью. В этом случае позиция тела меняется пропорционально времени, и производная будет постоянной. Если же скорость меняется, то производная будет зависеть от времени и позволяет определить, как быстро меняется скорость.
Производная уравнения движения: понятие и его суть

Уравнение движения описывается как функция, где положение тела зависит от времени. Производная этой функции по времени дает нам скорость, с которой тело меняет свое положение. Если взять производную скорости по времени, то получится ускорение, которое показывает, насколько быстро меняется скорость.
Производные уравнения движения являются важным инструментом для анализа и предсказания поведения физических систем. Они позволяют определить точки разворота, максимумы и минимумы функции, а также изучить особенности движения.
Рассмотрим пример, чтобы более понятно представить суть производной уравнения движения. Представим, что у нас есть автомобиль, который движется по прямой дороге. Его положение определяется функцией x(t), где x - расстояние от начала дороги, а t - время. Производная этой функции, dx/dt, даст нам скорость автомобиля, то есть сколько километров он проезжает за единицу времени.
Если мы возьмем производную скорости по времени, то получим ускорение автомобиля. Это покажет нам, насколько быстро автомобиль ускоряется или замедляется.
Таким образом, производная уравнения движения позволяет нам изучать и анализировать изменения положения, скорости и ускорения тела с течением времени, что является фундаментальным понятием в физике.
Производная в физике: ключевая концепция для описания движения
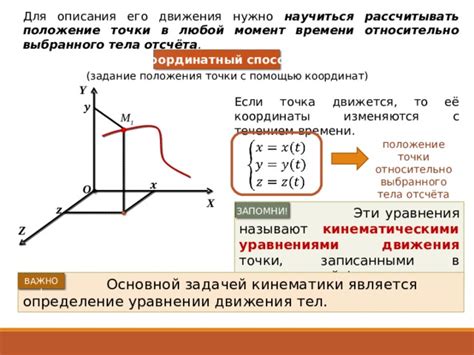
Производная функции, описывающей движение тела, показывает, какое изменение происходит в этой функции при изменении времени. В физике производная используется для определения скорости (первая производная) и ускорения (вторая производная) объекта.
Например, при анализе свободного падения объекта на Земле, мы можем использовать производную для определения скорости и ускорения падающего тела в зависимости от времени. Зная функцию, описывающую положение тела, мы можем вычислить ее производную, чтобы получить информацию о скорости изменения его положения и ускорении.
Производная также позволяет нам проводить сравнительный анализ и синтез различных движений, установить закономерности, связи и зависимости между ними. Она помогает нам понять и предсказать поведение физических систем, находить оптимальные решения и улучшать процессы в различных областях физики.
Таким образом, производная является ключевой концепцией в физике, позволяющей анализировать и описывать движение объектов. Ее использование позволяет получать информацию о скорости и ускорении объекта, а также выявлять закономерности и зависимости между различными движениями. Изучение производной в физике является неотъемлемой частью понимания и описания физических явлений в природе.
Примеры применения производной в задачах движения

Производная уравнения движения позволяет решать различные задачи, связанные с движением объектов. Рассмотрим несколько примеров применения производной в задачах движения:
Расчет скорости и ускорения
Производная уравнения движения позволяет найти скорость и ускорение объекта в каждый момент времени. Зная зависимость координаты объекта от времени, можно найти производные и получить значения скорости и ускорения в каждый момент времени.
Нахождение момента времени, когда скорость достигает максимума или минимума
Производная скорости по времени позволяет найти точки экстремума скорости. Подставляя значения времени в производную скорости и приравнивая ее к нулю, можно найти время, когда скорость достигает максимума или минимума.
Определение времени остановки или изменения направления движения
Производная скорости по времени также позволяет определить момент времени, когда скорость объекта становится нулевой или меняет свое направление. Эти моменты времени соответствуют моментам остановки или изменения направления движения.
Оценка расстояния пройденного объектом
Производная координаты по времени позволяет найти скорость объекта в каждый момент времени. Интегрирование этой скорости по времени позволяет оценить расстояние, которое объект пройдет за определенное время.
Построение траектории движения
Зная функцию зависимости координаты от времени, можно выразить координату через производные. Подставляя значения времени, можно получить точки траектории движения объекта. Это полезно для визуализации движения и изучения его характеристик.
Вычисление производных уравнений движения в различных ситуациях

Вычисление производных уравнений движения осуществляется с помощью математической операции дифференцирования. Она позволяет найти производную функции, которая описывает движение тела.
При вычислении производной уравнения движения необходимо учитывать конкретные условия и формулы для различных ситуаций. Например, для движения по прямой величина скорости вычисляется как производная по времени от функции координаты по времени. Для движения по окружности производные определяются через радиус и угловую скорость.
Также вычисление производных уравнений движения зависит от того, является ли тело материальной точкой или имеет массу и размеры. Для системы частиц или твердого тела используются соответствующие формулы и уравнения.
Производные уравнений движения находят широкое применение в физике, механике, аэродинамике и других областях науки. Они позволяют анализировать и предсказывать поведение объектов, описывать их траектории и взаимодействия с другими телами.
Важно отметить, что вычисление производных уравнений движения требует навыков работы с дифференциальными уравнениями и знаний математического аппарата. В некоторых случаях может потребоваться использование численных методов для аппроксимации производных и численного решения уравнений движения.