Корни являются одним из основных математических понятий, и их изучение неотъемлемо при решении различных задач. В контексте производных функций корни также играют важную роль, и эффективный способ их расчета может значительно облегчить математические вычисления.
Производная функции с корнем является важным инструментом при анализе поведения функций и определении их характеристик, таких как экстремумы, точки перегиба и определение области возрастания и убывания функции. Правильное вычисление производной с корнем позволяет получить точные результаты и более глубокое понимание свойств функции.
Одним из эффективных методов расчета производной функции с корнем является использование правила дифференцирования сложной функции. Для этого необходимо применить цепное правило, которое позволяет выразить производную функции с корнем через производную внутренней и наружной функции. Этот подход позволяет существенно упростить вычисления и получить более компактное выражение для производной.
Производные функций с корнем находят применение в множестве областей, включая физику, экономику, инженерию и статистику. Их правильный расчет является важным этапом решения различных задач, оптимизации функций и моделирования поведения систем. Правильное понимание методов расчета производных функций с корнем позволяет существенно повысить эффективность анализа данных и принятия решений в различных областях науки и техники.
Что такое производная функции?

Понятие производной является одной из основных и важных концепций математического анализа. Оно используется для исследования функций и решения различных задач из множества областей науки и техники.
Геометрически производная функции показывает, как быстро меняется значение функции по абсциссе. Если производная положительная, то функция возрастает. Если производная отрицательная, то функция убывает. Если производная равна нулю, то функция имеет экстремум (максимум или минимум).
Производная функции может быть найдена аналитически или численно. Методы аналитического нахождения производной включают в себя дифференцирование по правилам и теоремам математического анализа. Численные методы основаны на аппроксимации производной с помощью конечных разностей или интерполяции.
Производная функции с корнем является специальным случаем. В таком случае, для нахождения производной используются правила дифференцирования исходной функции, а затем производная в данной точке вычисляется численно или аналитически.
Знание производной функции позволяет множество применений, включая определение скорости и ускорения объектов, оптимизацию функций и решение задач физики, экономики и других наук.
Значение производной функции в точке
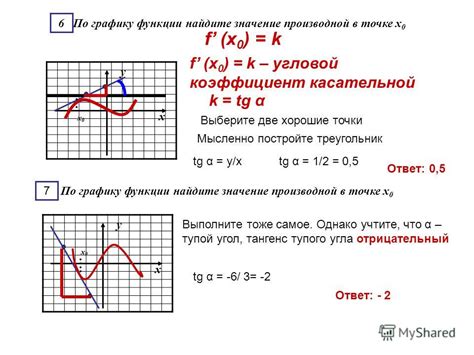
Производная функции в точке представляет собой скорость изменения значения функции в данной точке. Чтобы найти значение производной функции в определенной точке, необходимо:
- Вычислить производную функции с использованием соответствующих правил дифференцирования.
- Подставить значение точки в найденную производную функцию.
- Вычислить полученное выражение.
Это значение будет указывать на скорость изменения функции в данной точке. Если значение производной больше нуля, то функция возрастает в данной точке. Если значение производной меньше нуля, то функция убывает в данной точке. Если значение производной равно нулю, то функция имеет экстремальную точку.
Как найти производную функции с корнем?

Для нахождения производной функции с корнем необходимо использовать правило дифференцирования сложной функции.
- Если у нас имеется функция вида f(x) = √u(x), где u(x) - некоторая дифференцируемая функция, то ее производная будет равна:
f'(x) = (1 / 2√u(x)) * u'(x)
- Также можно использовать правило дифференцирования функции вида f(x) = (u(x))^n, где u(x) - дифференцируемая функция, а n - некоторое рациональное число. В этом случае производная будет равна:
f'(x) = n(u(x))^(n-1) * u'(x)
При применении данных правил необходимо помнить, что u(x) - это внутренняя функция, под корнем или в степени, а u'(x) - ее производная.
Найденная производная функции с корнем будет показывать, как изменяется значение функции при изменении аргумента.
Применение правила дифференцирования

Для эффективного расчета производных функций, содержащих корень, можно применять правило дифференцирования. Правило дифференцирования позволяет найти производную сложной функции с помощью производных простых функций.
Пример:
Рассмотрим функцию f(x) = √(3x - 2). Чтобы найти производную этой функции, используем правило дифференцирования.
Шаг 1: Запишем функцию в виде f(x) = (3x - 2)^(1/2).
Шаг 2: Применим правило дифференцирования к функции. Для этого умножим производную степенной функции на производную аргумента функции: f'(x) = (1/2)(3x - 2)^(-1/2) * 3.
Шаг 3: Упростим полученное выражение: f'(x) = 3/2(3x - 2)^(-1/2).
Таким образом, производная функции f(x) = √(3x - 2) равна f'(x) = 3/2(3x - 2)^(-1/2).
Применение правила дифференцирования позволяет эффективно находить производные функций с корнем, что является важным инструментом в анализе и оптимизации функций.
Преобразование функции в эквивалентную без корня
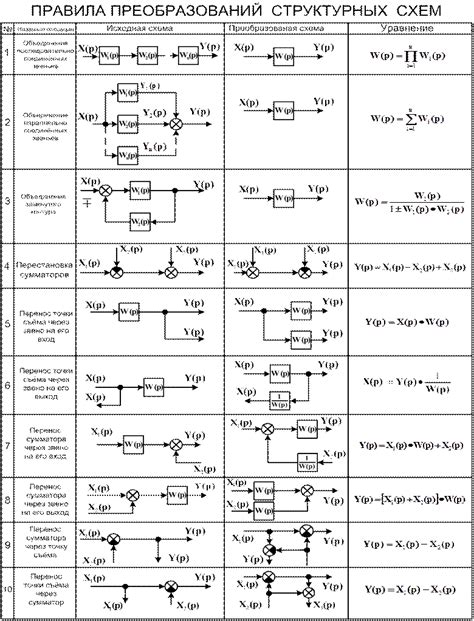
Для эффективного расчёта производных функций с корнем важно обратить внимание на возможность преобразования функции в эквивалентную без корня. Такое преобразование может значительно упростить расчёты и ускорить процесс нахождения производной.
Пусть у нас есть функция f(x) = √(g(x)), где g(x) - некоторая функция.
Для того чтобы преобразовать такую функцию в эквивалентную без корня, можно воспользоваться следующим способом:
Возведем обе части функции в квадрат:
f(x)² = (√(g(x)))²
Раскроем скобки:
f(x)² = g(x)
Отсюда получаем, что f(x)² = g(x). Теперь, чтобы получить функцию без корня, необходимо возвести обе части в приемлемую степень. Обычно выбирают степень 0.5 или 1/2, так как это позволяет избавиться от корня и сохранить исходную функцию.
Итак, (f(x)²)^0.5 = g(x)^0.5, что эквивалентно f(x) = g(x)^0.5. Таким образом, мы преобразовали функцию без корня в эквивалентную функцию с корнем.
Теперь, чтобы найти производную функции f(x) = √(g(x)), можно использовать правила производной для функции f(x) = g(x)^0.5, которая не содержит корня.
Преобразование функции в эквивалентную без корня позволяет эффективно рассчитывать производные функций с корнем, упрощает дальнейшие математические операции и делает процесс расчётов более понятным и удобным.
Преимущества рассчета производных функций с корнем в момент
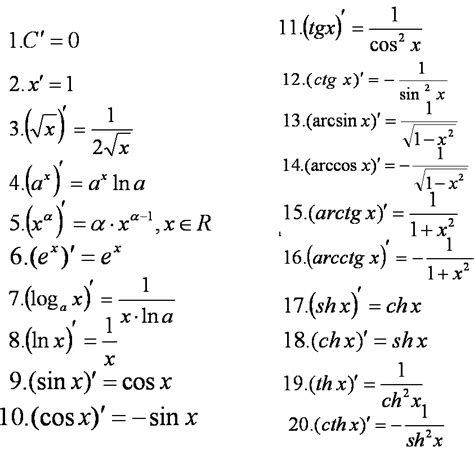
Рассчет производных функций с корнем в момент имеет несколько преимуществ, которые делают этот метод эффективным и удобным в использовании. Вот некоторые из них:
1. Скорость расчета Рассчет производной функции с корнем в момент может быть выполнен эффективно и быстро. Это особенно важно в случаях, когда функция содержит сложную формулу с использованием множества переменных и операций. | 2. Точность результатов Рассчет производных функций с корнем в момент позволяет получить точные результаты. Это особенно полезно, если мы хотим использовать эти производные в дальнейших расчетах или аналитических задачах. |
3. Упрощение формул Рассчет производных функций с корнем в момент может помочь упростить формулы и упростить дальнейшие вычисления. Это обусловлено тем, что корень входит в производную функции как степень и может быть обработан вместе с остальными частями формулы. | 4. Возможность оптимизации Расчет производных функций с корнем в момент может привести к оптимизации алгоритмов. Если мы можем рассчитать производную функции в реальном времени, то можем использовать полученные результаты для более эффективного управления и оптимизации процессов, использующих эту функцию. |
Расчет производных функций с корнем в момент является мощным инструментом, который позволяет получить точные результаты быстро и эффективно. Этот метод может быть очень полезен для ускорения аналитических задач, оптимизации алгоритмов и упрощения формул. Необходимо помнить, что в некоторых случаях может потребоваться использование других методов расчета производных функций, чтобы получить наиболее точные результаты.
Примеры расчета производных функций с корнем
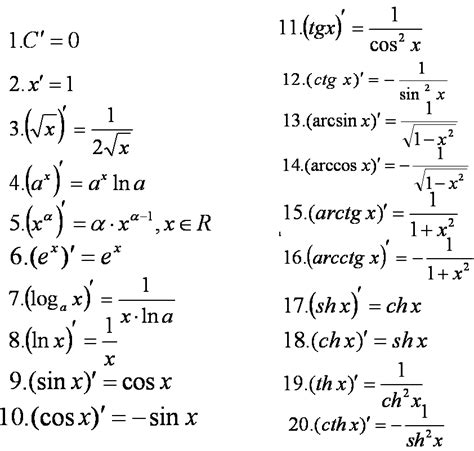
Для более наглядного понимания, рассмотрим примеры расчета производных функций с корнем:
Функция:
f(x) = \sqrt{x}Производная:
f'(x) = \frac{1}{2\sqrt{x}}Например, для
x = 4:f'(4) = \frac{1}{2\sqrt{4}} = \frac{1}{2 \cdot 2} = \frac{1}{4}Функция:
f(x) = \sqrt{x^2 + 1}Производная:
f'(x) = \frac{x}{\sqrt{x^2 + 1}}Например, для
x = 2:f'(2) = \frac{2}{\sqrt{2^2 + 1}} = \frac{2}{\sqrt{4 + 1}} = \frac{2}{\sqrt{5}}Функция:
f(x) = \sqrt[3]{x}Производная:
f'(x) = \frac{1}{3x^{\frac{2}{3}}}Например, для
x = 8:f'(8) = \frac{1}{3 \cdot 8^{\frac{2}{3}}} = \frac{1}{3 \cdot 4} = \frac{1}{12}
Производные функций с корнем позволяют находить скорость изменения величины и могут быть полезны в различных областях науки и техники.