Аксонометрическая проекция является одним из видов пространственных проекций и используется для изображения трехмерных объектов на плоскости. Одним из самых часто встречающихся объектов в трехмерном пространстве является эллипс.
Эллипс - это замкнутая кривая, которая представляет собой сечение поверхности конуса плоскостью. В отличие от окружности, у которой все точки равноудалены от одной точки, центра, эллипс имеет два фокуса, уникальные точки, сумма расстояний от которых до любой точки на эллипсе постоянна.
Для построения эллипса в аксонометрии необходимо знать значения двух радиусов - большого (a) и малого (b), а также выбрать угол наклона проекционной плоскости. Для начала необходимо нарисовать оси x и y, на которых будут располагаться точки эллипса.
Далее, для каждой точки эллипса (x, y) считаем значения по следующим формулам: x = a * cos(alpha), y = b * sin(alpha), где alpha - угол наклона проекционной плоскости. Повторяем эту операцию для достаточного количества точек, чтобы получить гладкую кривую. Затем соединяем полученные точки линией, получая эллипс.
Определение и особенности эллипса
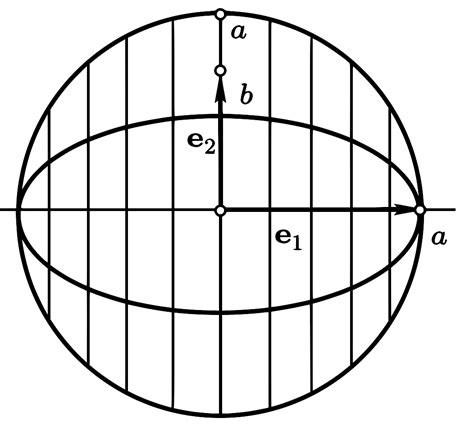
Основными характеристиками эллипса являются:
- Большая и малая полуоси - это отрезки, проведенные от центра эллипса до крайней точки кривой по горизонтали и вертикали соответственно;
- Фокусы - точки, для которых выполняется условие суммы расстояний;
- Центр - точка пересечения большой и малой полуосей;
- Эксцентриситет - отношение полуразности полуосей к их средней величине.
В аксонометрической проекции эллипса важным свойством является сохранение формы и размеров фигуры. Благодаря этому, эллипс может быть точно воссоздан в трехмерной системе координат без искажений искривлений.
Выбор системы координат для построения эллипса
При построении эллипса в аксонометрии необходимо выбрать подходящую систему координат. Существует несколько систем координат, которые могут быть использованы для этой задачи.
Одной из наиболее распространенных систем координат в аксонометрии является изометрическая система координат. В этой системе координат оси x и y образуют угол в 120 градусов, а ось z перпендикулярна плоскости xy. Изометрическая система координат часто используется для построения эллипсов в аксонометрической проекции.
Другой вариант системы координат, который может быть использован при построении эллипса в аксонометрии, - это диметрическая система координат. В диметрической системе координат оси x и y образуют углы, не равные 120 градусам, что позволяет более гибко представлять объекты в трехмерном пространстве.
Выбор системы координат зависит от типа аксонометрической проекции и требуемых характеристик построения эллипса. Некоторые системы координат могут быть более удобными для определенных типов эллипсов или специфических задач.
| Система координат | Описание |
|---|---|
| Изометрическая | Оси x и y образуют угол в 120 градусов, ось z перпендикулярна плоскости xy |
| Диметрическая | Оси x и y образуют углы, не равные 120 градусам |
Выбор системы координат для построения эллипса в аксонометрии может быть важным шагом, определяющим визуальные характеристики конечного результата.
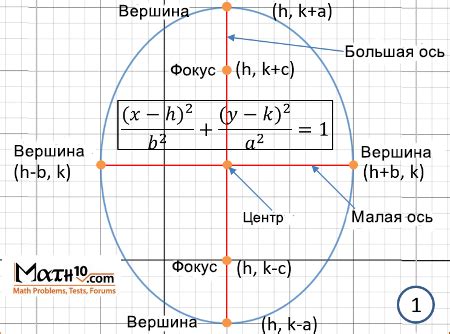
Определение полуосей эллипса
Для определения полуосей эллипса необходимо знать его главные размеры - длину большей полуоси и длину меньшей полуоси. Определить эти размеры можно различными способами, в зависимости от доступной информации.
Если известны фокусное расстояние эллипса и его эксцентриситет, полуоси можно найти по формулам:
a = f / e
b = a * sqrt(1 - e^2)
где f - фокусное расстояние, e - эксцентриситет.
Если известны длины большой оси (a) и малой оси (b), можно найти фокусное расстояние (f) по формуле:
f = sqrt(a^2 - b^2)
В некоторых случаях, когда известны другие геометрические параметры эллипса, можно применить специальные формулы для вычисления полуосей.
Определение полуосей эллипса является важным шагом в построении и изучении данной геометрической фигуры в аксонометрии. Зная полуоси, можно определить координаты всех точек эллипса и построить его в трехмерном пространстве.
Построение границы эллипса по полуосям и центру

Для построения границы эллипса в аксонометрии необходимо знать длины полуосей и координаты его центра. Полуоси эллипса обозначаются как a (горизонтальная полуось) и b (вертикальная полуось), а центр эллипса указывается координатами xc и yc.
Используя полученные данные, можно построить границу эллипса следующим образом:
- Найти начальную точку границы эллипса. Для этого необходимо вычислить координаты x и y для угла 0° (или 360°) относительно центра эллипса, используя параметрическое уравнение эллипса.
- С помощью полученных координат и применяя различные углы (обычно с шагом 1°), нарисовать линию, соединяющую начальную точку с остальными точками границы эллипса.
- Повторить шаг 2 для каждого угла, пока не будет нарисована полная граница эллипса.
После выполнения этих шагов получится граница эллипса в аксонометрии. Она будет представлять из себя замкнутую кривую с гладкими переходами между точками.
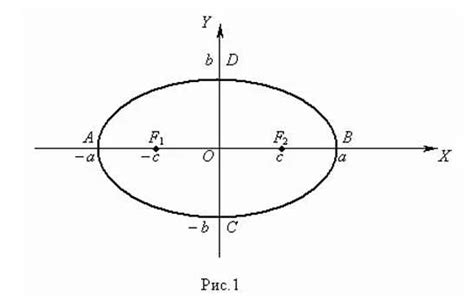
Построение внутренней структуры эллипса

Для построения эллипса в аксонометрии необходимо определить его внутреннюю структуру. Внутренняя структура эллипса состоит из его основных элементов, таких как фокусы, оси и вершины.
Фокусы эллипса представляют собой точки на его оси, которые расположены симметрично относительно центра эллипса. Фокусы играют важную роль при построении эллипса, так как от них определяется форма и размер эллипса.
Оси эллипса являются его симметричными осями, которые пересекаются в центре эллипса. Оси определяют направление и наклон эллипса.
Вершины эллипса представляют собой точки на его периферии, которые находятся на равном расстоянии от центра эллипса. Вершины эллипса определяют его форму и окружность.
При построении внутренней структуры эллипса, необходимо учитывать его размеры и пропорции. Фокусы и вершины должны быть правильно расположены относительно центра эллипса, чтобы сохранить правильную форму и окружность.
Построение внутренней структуры эллипса является важным этапом в его создании в аксонометрии. Корректное определение фокусов, осей и вершин эллипса позволит достичь точности и реалистичности в его представлении.
Использование соотношения сторон для создания реалистичного эллипса

Для создания реалистичного эллипса в аксонометрии нужно отобразить его форму в соответствии с тем, какой проекции подвергается объект. Для изометрической проекции, где углы между осями составляют 120 градусов, будет использоваться следующее соотношение сторон: основная ось A будет иметь вдвое больший размер, чем вторичная ось B и побочная ось C. Такое соотношение позволяет создать эллипс, который будет восприниматься глазом как плоская фигура.
При создании эллипса в аксонометрии можно использовать следующие шаги:
- Найдите центр эллипса и определите его размеры.
- Используя определенные размеры, нарисуйте прямоугольник, в котором эллипс будет находиться. Учтите соотношение сторон, чтобы создать реалистичное изображение.
- Соедините противоположные углы прямоугольника дугами, чтобы создать кривую форму эллипса.
- Стилизуйте эллипс, добавив цветовое заполнение или обводку в соответствии с вашими предпочтениями.
При дальнейшей работе с аксонометрическими эллипсами, не забывайте, что пропорции и соотношения размеров могут варьироваться в зависимости от выбранной проекции и желаемого эффекта. Экспериментируйте с разными соотношениями сторон и формами, чтобы создавать уникальные и реалистичные эллипсы.
Добавление теней и оттенков для придания объемности эллипсу

Добавление теней и оттенков к эллипсу может помочь придать ему ощущение объемности и глубины. С помощью некоторых техник и эффектов можно создать реалистичные и эстетически привлекательные эллипсы в аксонометрической проекции.
Одним из способов добавить тени и оттенки является использование градиентных заливок. Градиентные заливки создают иллюзию объемности, отображая светлые и темные области на эллипсе.
Для создания градиентной заливки вы можете использовать CSS-свойство "background-image" и указать градиентный фоновый рисунок. Выберите цвета, которые вы хотите использовать в градиенте, и определите направление, в котором они будут изменяться. Например, вы можете использовать вертикальный или горизонтальный градиент.
Еще одним способом добавления теней и оттенков является использование теневых эффектов CSS. Теневые эффекты позволяют добавить тень к форме эллипса, что делает его более реалистичным и объемным. Для создания теней вы можете использовать CSS-свойство "box-shadow" и определить цвет, смещение и размытие тени.
Применение этих техник и эффектов может значительно улучшить визуальный вид вашего эллипса в аксонометрической проекции. Эти методы помогут создать объемный эффект и добавить реалистичность к вашим графическим изображениям.
