Построение графика функции – это одна из основных задач в математике и сопряженных ей науках. Знание этого процесса является ключевым, если вы хотите понять поведение функции, найти ее точные значения и проанализировать ее свойства.
В этом руководстве мы расскажем о том, как шаг за шагом построить график функции. Мы охватим такие важные аспекты, как определение области значений, построение таблицы значений, выбор точек для построения графика, построение осей координат и самого графика. Здесь вы найдете полезные советы и инструкции, которые помогут вам справиться с этой задачей.
Прежде чем начать построение графика, важно понять, что такое функция и как она работает. Функция представляет собой математическую зависимость между двумя величинами, где каждому значению одной величины соответствует единственное значение другой величины. График функции – это способ визуализации этой зависимости.
Теперь давайте перейдем к построению графика. Первым шагом является определение области значений функции – интервала, в котором определена функция. Это позволит вам определить, в каких пределах вы будете строить график. Затем, построив таблицу значений, вы сможете получить некоторые значения функции, используя разные значения аргумента. Далее, выбрав достаточное количество точек на оси координат, вы сможете построить проводник для графика функции.
Простое руководство по построению графика функции
Вот шаги, которые вам нужно выполнить для построения графика функции:
1. Задайте диапазон значений для переменной
Первым шагом в построении графика функции является задание диапазона значений для переменной. Диапазон может быть задан вручную или с использованием математической формулы. Например, если вы строите график функции y = x^2, вы можете выбрать диапазон значений для переменной x от -10 до 10.
2. Вычислите значения функции
Вторым шагом является вычисление значений функции для каждого значения переменной в заданном диапазоне. Для функции y = x^2, вычислите значение y для каждого значения x в заданном диапазоне. Например, если x = 2, то y = 2^2 = 4.
3. Постройте координатную плоскость
Третий шаг - построение координатной плоскости, на которой будет отображен график функции. Разделите плоскость на оси x и y, используя клетки или отметки. Отметьте нулевые точки на оси x и y.
4. Постройте график функции
Четвертый и последний шаг - построение графика функции. Используя значения функции, вычисленные на втором шаге, отметьте соответствующие точки на координатной плоскости. Затем соедините эти точки линией, чтобы получить график функции.
Следуя этим простым шагам, вы сможете построить график функции для любой математической функции. Не забывайте, что практика - лучший способ улучшить свои навыки, поэтому не стесняйтесь экспериментировать и строить графики различных функций.
Выбор функции
При построении графика функции важно правильно выбрать функцию, которую вы будете анализировать и отображать на графике. Выбор функции зависит от задачи или вопроса, на который вы хотите получить ответ.
Вот несколько общих советов для выбора функции:
| Тип функции | Описание | Примеры |
|---|---|---|
| Линейная функция | Функция, которая имеет форму прямой линии. | y = 2x + 3 |
| Квадратичная функция | Функция, которая имеет форму параболы. | y = x^2 + 4x + 5 |
| Тригонометрическая функция | Функция, которая связана с тригонометрическими операциями. | y = sin(x) |
| Экспоненциальная функция | Функция, которая имеет форму экспоненты. | y = 2^x |
Выбор функции также зависит от вашего уровня знаний и умений работы с математикой. Если вы только начинаете заниматься построением графиков, рекомендуется выбрать простую функцию, чтобы легче разобраться в процессе.
Запомните, что функции могут быть очень разнообразными, и выбор правильной функции поможет вам получить нужную информацию из графика. Выбор функции - первый и один из самых важных шагов в процессе построения графика функции.
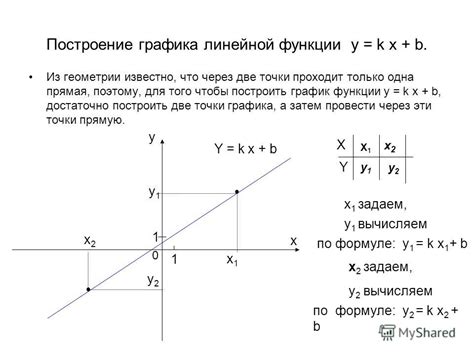
Построение координатной плоскости

Для начала, создадим таблицу, в которой разместим оси координат. Ось абсцисс будет горизонтальной прямой, а ось ординат - вертикальной. Они будут пересекаться в точке (0,0), которая называется началом координат.
| Y | |
| X |
Далее, нарисуем отрезки на каждой из осей, которые будут представлять определенные диапазоны значений. Выбор диапазона зависит от функции, график которой мы строим.
На оси абсцисс, мы обычно размещаем значения аргумента функции, а на оси ординат - значения самой функции. Обратите внимание, что отрицательные значения аргумента и функции тоже могут присутствовать на координатной плоскости.
Также не забудьте пометить деления на осях и подписать их. Подписи осей абсцисс и ординат - это названия самих осей.
После завершения построения координатной плоскости, вы готовы приступить к построению графика функции. Вам достаточно будет знать значения функции в определенных точках и соединить их линиями. Обычно, чем больше точек используется для построения графика, тем более точным он будет.
Определение области определения и значения функции

Для определения области определения функции необходимо учесть ограничения, наложенные на переменные и операторы функции. Вначале нужно исследовать все переменные в функции и определить, какие значения они могут принимать. Затем следует учесть все операторы и функции, применяемые внутри функции, и учесть их ограничения.
Значения функции представляются в виде упорядоченных пар (x, y), где x - входное значение из области определения, а y - соответствующее выходное значение. Для построения графика достаточно выбрать несколько значений из области определения и вычислить соответствующие значения функции.
Имеется несколько способов определения области определения и значений функции. Один из способов - аналитический, при котором анализируются уравнения и ограничения, накладываемые на переменные и операторы функции. Другой способ - графический, при котором строится график функции и определяются область определения и значения функции по форме и свойствам графика.
Важно помнить, что область определения и значения функции могут быть ограничены физическими или математическими ограничениями, включая значение переменной, домен функции или ограничения на входные или выходные значения. Также необходимо учесть возможные асимптоты и точки разрыва функции при определении области определения и значений.
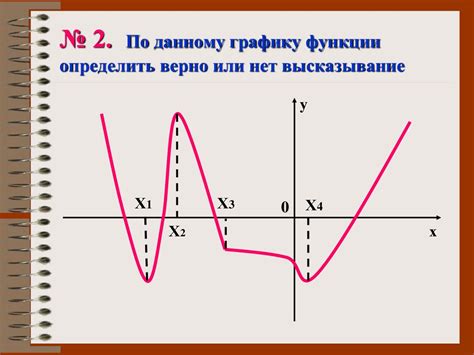
Нахождение точек пересечения с осями координат
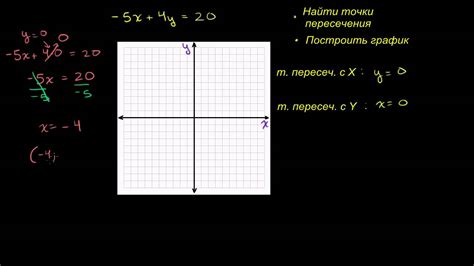
Для построения графика функции важно знать точки, где график пересекает оси координат. Эти точки, также называемые нулями функции, могут быть полезными для определения поведения функции и анализа ее свойств.
Чтобы найти точки пересечения с осью OX (горизонтальной осью), нужно решить уравнение функции f(x) = 0. Для этого приравняйте выражение функции к нулю и найдите значения переменной x, при которых это равенство выполняется. Такие значения x будут соответствовать точкам пересечения графика с осью OX.
Аналогично, чтобы найти точки пересечения с осью OY (вертикальной осью), нужно решить уравнение x = 0. Здесь нет функции, поэтому вместо этого вертикальная прямая задается уравнением значения x равно нулю. Точки, в которых график функции пересекает эту прямую, будут точками пересечения с осью OY.
Чтобы найти точку пересечения графика с осью OX, вам понадобится табличка:
| № | x | f(x) |
|---|---|---|
| 1 | x1 | f(x1) |
| 2 | x2 | f(x2) |
| 3 | x3 | f(x3) |
| ... | ... | ... |
Функция f(x) может быть представлена в виде аналитического выражения или задана при помощи значений в табличной форме, которые можно получить, подставляя различные значения x. Выберите разумный диапазон значений x, чтобы покрыть область интересующего вас графика.
Точки пересечения с осью OY могут быть найдены при помощи графика, представленного в координатной плоскости. Найдите точку пересечения графика с вертикальной прямой, соответствующей уравнению x = 0. Значение y в этой точке будет являться точкой пересечения с осью OY.
Зная эти точки пересечения с осями координат, вы можете использовать их для построения графика функции и анализа его свойств, таких как возрастание и убывание функции, наличие экстремумов и асимптот.
Таким образом, нахождение точек пересечения с осями координат является важным шагом в построении графика функции.
Построение графика функции по особым точкам
Когда мы строим график функции, основная задача состоит в том, чтобы указать, как функция меняется при изменении значения переменной. Однако, помимо обычных точек, функция может иметь так называемые "особые точки". Это точки, в которых функция может обнаружиться, быть неопределенной или изменять свое поведение.
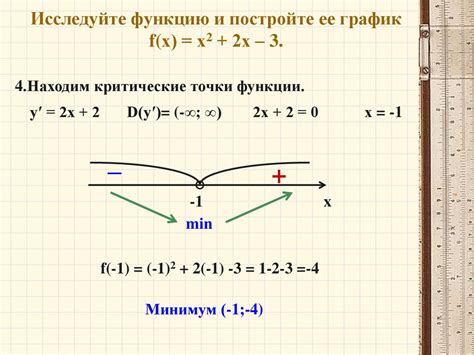
Особые точки могут быть разными: точки разрыва, экстремумы (максимумы и минимумы), нули функции и асимптоты. Построение графика функции по особым точкам требует дополнительного внимания и анализа.
Чтобы построить график функции по точкам разрыва, нужно определить, почему разрыв возникает и как он выглядит. Разрыв может быть конечным (когда функция неопределена в конкретных точках) или бесконечным (когда функция стремится к бесконечности в определенных точках).
Поиск экстремумов функции важен, чтобы определить, где функция достигает своих максимальных и минимальных значений. Экстремумы могут быть локальными (когда значения функции наименьшие или наибольшие в некоторой окрестности точки) или глобальными (когда значения функции наименьшие или наибольшие на всем интервале значений).
Нули функции – это значения переменной, при которых функция равна нулю. Нули функции можно определить, приравняв функцию к нулю и решив уравнение. Нули обозначают пересечения графика функции с осью x.
Асимптоты функции – это линии или кривые, которые приближаются к графику функции в бесконечности или приближаются к нему насколько близко, насколько это возможно. Асимптоты могут быть вертикальными, горизонтальными или наклонными.
Итак, при построении графика функции по особым точкам необходимо учитывать разрывы, экстремумы, нули и асимптоты. Тщательный анализ всех этих особых точек позволит получить полную картину поведения функции и построить точный и информативный график.
Соединение точек и окончательное построение графика функции
После того, как вы построили все точки на координатной плоскости в соответствии с значениями функции, настало время соединить их линиями и получить окончательный график функции.
Соединение точек является важным шагом в построении графика функции. Это позволяет визуализировать зависимость между значениями функции и ее аргументами.
Один из способов соединить точки - это провести прямые линии между ними. Если точки находятся в диапазоне значений, где функция увеличивается, линия должна быть направлена вверх, а если функция уменьшается - вниз.
Если значения функции между точками не меняются линейно, то может потребоваться применение кривой линии для соединения точек, чтобы учесть эту изменчивость функции.
Каким бы способом соединения точек вы ни выбрали, важно, чтобы график функции был плавным и непрерывным. Чем более точно вы соединяете точки, тем более точным и информативным становится график функции.
После того, как вы связали все точки линиями, ваша функция полностью визуализирована и готова к анализу. Вы можете использовать график функции для определения ее основных характеристик, таких как пересечения с осями, экстремумы, изменение роста и убывания функции и т. д.
Не забудьте добавить заголовок и подписи к осям координат, чтобы понятно указать, к каким значениям относятся оси и какое уравнение соответствует графику.