Треугольник является одной из самых простых и распространенных геометрических фигур. Но для того, чтобы выполнить элементарные вычисления, такие как нахождение периметра или длины сторон треугольника, необходимо знать некоторые основные принципы и формулы.
Периметр треугольника представляет собой сумму длин его сторон. Для его вычисления необходимо знать длины всех трех сторон треугольника. Однако, далеко не всегда эта информация известна сразу и требуется найти ее по другим данным, например, по известным длинам двух сторон и углу между ними.
Для нахождения длины сторон треугольника существуют различные методы и формулы. Один из самых распространенных методов - теорема косинусов. Согласно этой теореме, квадрат длины одной стороны треугольника равен сумме квадратов длин двух других сторон, умноженных на два произведения этих сторон и косинус угла между ними.
Периметр треугольника: определение и принцип расчета
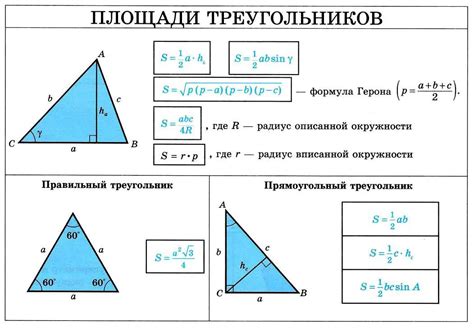
Первым шагом необходимо измерить длины всех сторон треугольника. Если известны только координаты вершин треугольника, то длины сторон могут быть рассчитаны с помощью теоремы Пифагора или формулы расстояния между точками на плоскости.
Для расчета периметра треугольника необходимо сложить длины всех его сторон:
| Сторона | Длина |
|---|---|
| AB | a |
| BC | b |
| AC | c |
Периметр треугольника можно обозначить как:
P = a + b + c
Где a, b и c – длины сторон треугольника.
Зная значения длин сторон, можно легко рассчитать периметр треугольника и использовать его в дальнейших расчетах или задачах.
Методы расчета периметра треугольника

1. Если известны длины всех сторон треугольника, то периметр можно найти, просто сложив эти длины:
периметр = a + b + c
где a, b, c - длины сторон треугольника.
2. Если известны координаты вершин треугольника в декартовой системе координат, то периметр можно найти, используя формулу длины отрезка по координатам:
периметр = AB + BC + AC
где AB, BC, AC - длины сторон треугольника, которые рассчитываются по формуле:
AB = sqrt((x₂-x₁)² + (y₂-y₁)²)
BC = sqrt((x₃-x₂)² + (y₃-y₂)²)
AC = sqrt((x₃-x₁)² + (y₃-y₁)²)
где x₁, y₁, x₂, y₂, x₃, y₃ - координаты вершин треугольника.
3. Если известны длины двух сторон треугольника и угол между ними, то периметр можно найти, зная закон косинусов:
периметр = a + b + c
где a, b - длины сторон треугольника, c - длина третьей стороны, которая рассчитывается по формуле:
c = sqrt(a² + b² -2ab*cos(угол))
где угол - угол между сторонами a и b.
Используя данные методы, вы сможете легко найти периметр треугольника в различных ситуациях.
Определение и расчет длины сторон треугольника
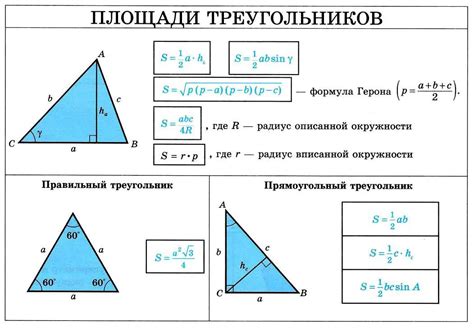
Существует несколько методов для расчета длины сторон треугольника. Один из наиболее распространенных методов основан на использовании теоремы Пифагора. Согласно этой теореме, в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Чтобы применить эту теорему к произвольному треугольнику, необходимо сначала определить его тип. Затем, используя известные длины сторон и углы треугольника, можно вычислить длину неизвестной стороны, применяя соответствующие геометрические формулы.
Другим методом расчета длины сторон треугольника является использование формулы расстояния между двумя точками в пространстве. Если известны координаты вершин треугольника, то можно вычислить длину каждой его стороны, применяя данную формулу. Данный метод основан на представлении треугольника в декартовой системе координат и использовании координатных выражений для вычисления расстояния между точками.
В зависимости от изначально имеющейся информации и задачи, различные методы определения и расчета длины сторон треугольника могут быть более удобными или точными. Важно учитывать геометрические особенности треугольника и выбрать наиболее подходящий метод для его измерения и анализа.
Свойства треугольника
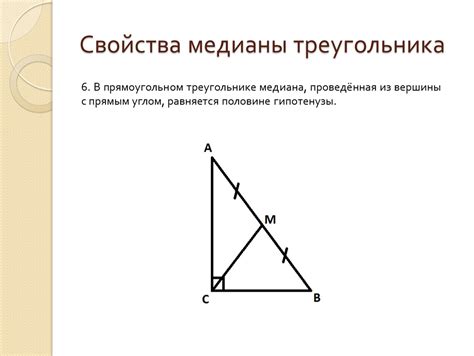
Периметр треугольника - это сумма длин всех его сторон. Чтобы найти периметр, нужно сложить длины всех трех сторон треугольника.
Треугольник равносторонний, если все его стороны равны. В таком треугольнике все углы также будут равными и составлять по 60 градусов.
Треугольник прямоугольный, если один из его углов равен 90 градусов. В прямоугольном треугольнике одна из сторон будем называть гипотенузой, а две другие - катетами.
Треугольник разносторонний - это треугольник, у которого все три стороны имеют разные длины.
Треугольник равнобедренный, если у него две стороны равны. Равнобедренный треугольник имеет два равных угла.
Изучение свойств треугольника позволяет нам более точно определить его характеристики и использовать эти знания при решении геометрических задач.
Основные свойства треугольника
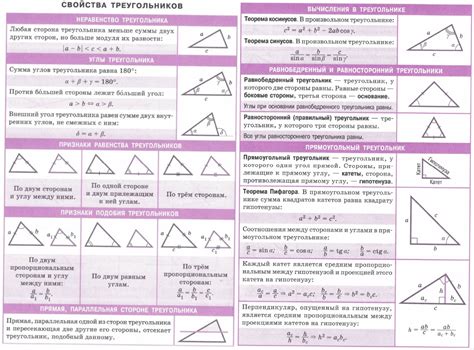
В треугольнике существуют несколько основных свойств:
| Стороны треугольника | Строение треугольника определяется длиной его трех сторон. Каждая сторона представляет отрезок между двумя вершинами треугольника. |
| Углы треугольника | Треугольник имеет три угла, расположенных между его сторонами. Сумма всех углов треугольника всегда равна 180 градусам. |
| Периметр треугольника | Периметр треугольника – это сумма длин всех его сторон. Чтобы найти периметр треугольника, нужно сложить длины всех его сторон. |
| Высота треугольника | Высота треугольника – это отрезок, проведенный из одной вершины треугольника к противоположной стороне и перпендикулярный ей. Высота может быть определена для каждой из сторон треугольника. |
Зная основные свойства треугольника, мы можем использовать их для расчета его периметра и длины сторон и решения различных геометрических задач, связанных с треугольниками.
Свойства равностороннего треугольника
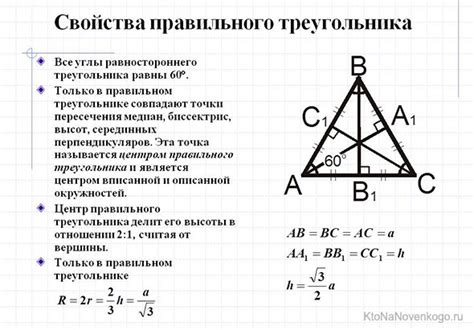
Основные свойства равностороннего треугольника:
- Все стороны равны между собой.
- Все углы равны между собой и равны 60 градусам.
- Высота, проведенная из вершины равностороннего треугольника, является биссектрисой и медианой, а также делит треугольник на два равнобедренных треугольника.
- Радиус вписанной окружности равностороннего треугольника равен половине одной из его сторон, а радиус описанной окружности равен трети стороны.
Эти свойства позволяют нам легко находить периметр равностороннего треугольника (путем умножения длины одной стороны на 3) и длину его сторон (путем деления периметра на 3).