Циркуль – это геометрический инструмент, который позволяет проводить окружности. Но что делать, если циркуль недоступен или потерялся, а задача требует найти центр окружности? В данной статье мы рассмотрим несколько методов, которые помогут решить эту проблему.
Первый метод основан на взаимном пересечении двух окружностей. Для этого необходимо провести две окружности, центры которых лежат на одной прямой и известны расстояния между центрами и точками пересечения с известной окружностью. Затем, найдя точки пересечения, соединяем их прямой. Полученная прямая будет проходить через центр искомой окружности.
Еще один метод основан на использовании перпендикуляров. Для этого необходимо возложить искомую окружность внутри треугольника и провести перпендикуляры к его сторонам. Точка их пересечения будет центром искомой окружности.
Также можно воспользоваться метрическим способом, если известны длины отрезков, соединяющих центр окружности с точками на ней. Этот способ основан на свойствах окружности и позволяет определить координаты центра окружности без использования циркуля.
Есть ли способы
Вопрос о том, как найти центр окружности без циркуля, вызывает много интереса. И действительно, существует несколько методов, которые позволяют найти центр окружности при помощи простых геометрических инструментов.
Один из таких методов – метод «треугольника». Для его осуществления достаточно провести две хорды в окружности и найти их точку пересечения. Эта точка будет являться центром окружности.
Еще один способ – метод с помощью окружностей. Для этого необходимо провести две любые хорды в окружности и найти их середины. Затем провести окружности, центры которых совпадают с серединами хорд. Пересечение этих окружностей будет точкой, при помощи которой можно определить центр окружности.
Однако следует помнить, что эти методы не всегда могут быть точными. Некоторые факторы, такие как погрешность измерений и неровности поверхности, могут влиять на точность найденного результата. Поэтому при использовании данных методов необходимо быть внимательным и учитывать возможные ошибки.
Определить центр окружности
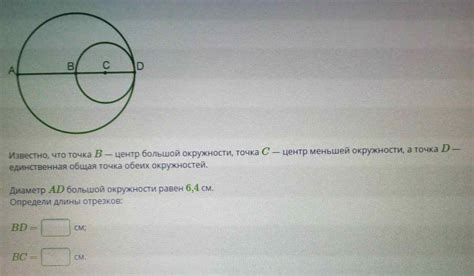
Определить центр окружности можно с помощью нескольких способов:
- Используя перпендикуляры: проведите два перпендикуляра к двум отрезкам окружности. Их пересечение будет являться центром окружности.
- Используя равные отрезки: выберите несколько точек на окружности и измерьте расстояние от каждой точки до остальных. Центр окружности будет находиться в точке, где все эти расстояния будут одинаковыми.
- Используя углы: проведите две хорды окружности и измерьте углы, образованные этими хордами и диаметральной прямой. Центр окружности будет находиться в точке, где эти углы будут равными.
- Используя теорему о перпендикулярных биссектрисах: проведите две хорды окружности и две их перпендикулярные биссектрисы. Их пересечение будет являться центром окружности.
Важно помнить, что для определения центра окружности необходимо иметь достаточное количество известных точек или отрезков на самой окружности.
Точки на окружности
1. Диаметр
Диаметр окружности является отрезком, соединяющим две точки на самой окружности и проходящим через центр. Диаметр является самой длинной хордой окружности и всегда делит окружность на две равные половины.
2. Хорда
Хорда - отрезок, соединяющий две точки на окружности. Отрезок, соединяющий крайние точки хорды и проходящий через центр окружности, называется диаметром.
3. Секущая
Секущая - прямая, которая пересекает окружность в двух различных точках. Если секущая не проходит через центр окружности, то она называется хордой. Если секущая проходит через центр окружности, то она является диаметром.
4. Касательная
Касательная - прямая, которая касается окружности в одной точке. Касательная всегда перпендикулярна радиусу, проведенному из центра окружности в точку касания.
5. Дуга
Дуга - часть окружности, ограниченная двумя её точками. Дуга может быть частью окружности или целой окружностью, в зависимости от числа точек, открывающихся на ней.
Знание основных свойств и характеристик точек на окружности позволяет легче разбираться в различных геометрических задачах, связанных с окружностями.
Основной признак

Для нахождения центра окружности, следует провести перпендикуляр к хорде, используя центр хорды. Затем, продлить этот перпендикуляр до пересечения с окружностью. Точка пересечения будет являться центром окружности. Таким образом, основным признаком для нахождения центра окружности без циркуля является перпендикуляр, проведенный из середины хорды.
Этот метод особенно полезен, когда нет возможности использовать циркуль или другие инструменты для построения окружностей. Он позволяет найти центр окружности с высокой точностью и достаточно прост в выполнении, требуя только рисования прямых и построения перпендикуляров.
Метод перпендикуляров
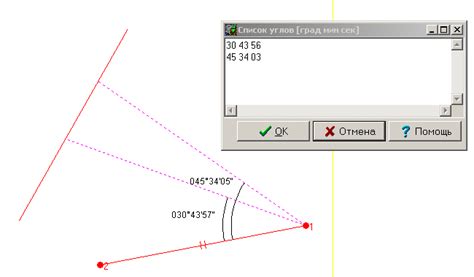
Для применения этого метода необходимо провести два перпендикуляра к сторонам окружности или к диаметрам. В результате пересечения этих перпендикуляров будет получен центр окружности.
Для начала выбирается одна сторона или диаметр окружности. Затем, в произвольной точке этой стороны или диаметра, проводится перпендикуляр. После этого выбирается вторая сторона или диаметр окружности, и из произвольной точки этой стороны или диаметра также проводится перпендикуляр.
После проведения обоих перпендикуляров, их пересечение определяет центр окружности. В этой точке можно провести окружность с радиусом, равным расстоянию от центра до любой точки окружности.
Метод перпендикуляров позволяет визуально находить центр окружности и применяется в различных областях, таких как геометрия, архитектура и дизайн. Этот метод основан на простых геометрических принципах и может быть использован без специального оборудования.
Построение перпендикуляров

Для построения перпендикуляра к данной прямой или отрезку необходимо следовать следующим шагам:
- Выбрать точку, через которую должен проходить перпендикуляр. Обозначим ее как точку A.
- Соединить точку A с конечной точкой прямой или отрезка. Получится отрезок AB.
- Создать окружность с центром в точке A и проходящую через точку B.
- Построить две дуги окружности на противоположных сторонах от отрезка AB.
- Используя эти две дуги как радиус, провести две пересекающиеся линии от точки B и их пересечение будет являться точкой, в которой пересекаются перпендикуляры.
Таким образом, мы можем построить перпендикуляры без использования циркуля и получить точку пересечения этих перпендикуляров, которая будет служить центром окружности.