Excel – многофункциональное программное обеспечение, способное решать разнообразные задачи, включая анализ данных и построение графиков. Одним из удобных инструментов, предоставляемых Excel, является возможность построения плоскости по уравнению, что позволяет наглядно визуализировать математические функции и определить их поведение на плоскости.
Для построения плоскости в Excel необходимо знание уравнения плоскости и правила построения графиков. Основным компонентом уравнения плоскости являются коэффициенты A, B, C и свободный член D, задающие положение и форму плоскости. Например, уравнение плоскости может иметь вид Ax + By + Cz + D = 0, где x, y, z – переменные, а A, B, C, D – коэффициенты.
Для начала работы с Excel создайте новую таблицу и введите значения переменных x и y в двух отдельных столбцах. Затем создайте новый столбец, в котором будет указано значение функции в соответствующей точке плоскости, заданной уравнением. Для вычисления значения функции воспользуйтесь формулой, в которой будут использованы значения переменных и коэффициенты уравнения плоскости.
Определение плоскости в Excel: основные шаги
Excel предоставляет мощный инструментарий для работы с данными и построения различных графиков включая плоскости. Определение плоскости в Excel происходит по шагам, которые помогут вам визуализировать вашу модель.
Шаг 1: Создайте новую таблицу в Excel и введите данные своей модели плоскости. Первый столбец будет содержать значения x, второй - y, а третий - z.
Шаг 2: Выделите данные вашей модели плоскости и откройте вкладку "Вставка" в верхней панели инструментов Excel. В разделе "Диаграммы" выберите тип графика "Плоскость" или "3D-плоскость".
Шаг 3: Построение плоскости осуществляется автоматически при выборе типа графика "Плоскость" или "3D-плоскость". Вы можете видеть плоскость, отображающуюся на графике согласно введенным данным.
Шаг 4: Дополнительно можно настроить оси координат и масштаб графика. Для этого выделите график и откройте вкладку "Конструктор графиков" в верхней панели инструментов Excel. В этом разделе вы сможете настроить различные параметры плоскости, такие как цвет, прозрачность и режим отображения.
Шаг 5: Сохраните вашу модель плоскости, чтобы иметь возможность продолжить работу над ней в Excel или поделиться ею с другими пользователями.
Теперь вы знаете основные шаги определения плоскости в Excel. С помощью этого инструмента вы сможете создать впечатляющие визуализации и анализировать свои данные более эффективно.
Знакомство с уравнением плоскости

Уравнение плоскости обычно записывается в виде:
- Аx + By + Cz + D = 0
где А, B и C - это коэффициенты, которые определяют наклон плоскости, а D - свободный член.
Если уравнение плоскости записано в канонической форме, то нормальный вектор к плоскости определяется коэффициентами A, B и C.
Чтобы построить плоскость в Excel, необходимо знать ее уравнение и использовать эти коэффициенты для создания графического представления плоскости.
Построение плоскости в Excel может быть полезным для визуализации данных, создания графиков или решения задач, связанных с плоскостью.
Приведенная ниже формула является примером демонстрации уравнения плоскости:
- 3x + 2y - z + 4 = 0
Используя эту формулу, вы можете построить плоскость с помощью Excel, задавая значения x, y и z и находя соответствующее значение z в уравнении.
Определение уравнения плоскости и его применение в Excel поможет вам выявить закономерности и взаимосвязи между данными и провести более точный анализ ваших исследований или экспериментов.
Создание нового листа в Excel
Чтобы создать новый лист в Excel, выполните следующие шаги:
- Откройте свой файл Excel и выберите вкладку "Лист" в верхней части окна программы.
- Щелкните правой кнопкой мыши на существующем листе и выберите опцию "Вставить".
- В открывшемся окне выберите тип нового листа (лист рабочей книги, лист диаграммы и т. д.) и нажмите кнопку "ОК".
После выполнения этих шагов в вашем файле Excel будет создан новый лист. Вы можете дать ему имя, щелкнув правой кнопкой мыши на названии листа и выбрав опцию "Переименовать".
Создание нового листа позволяет вам организовать данные по разным категориям и оси анализа, делая вашу работу в Excel более удобной и эффективной. Используйте эту функцию, чтобы легко отслеживать и обрабатывать информацию в своих таблицах.
Ввод данных в таблицу
Для построения плоскости по уравнению в Excel необходимо ввести данные в таблицу. Это можно сделать следующим образом:
Шаг 1: Откройте программу Excel и создайте новую таблицу.
Шаг 2: Введите значения координат точек в столбцы. Например, для плоскости в трехмерном пространстве введите значения x, y и z в отдельные столбцы.
Шаг 3: Введите уравнение плоскости в виде формулы в отдельную ячейку. Например, если уравнение плоскости задано как ax + by + cz + d = 0, введите формулу "=a1*x + b1*y + c1*z + d1" в ячейку, где a1, b1, c1 и d1 - значения коэффициентов.
Шаг 4: Продолжайте вводить данные и формулы в таблицу до тех пор, пока не будут введены все необходимые значения.
После ввода данных в таблицу можно переходить к построению плоскости. Это можно сделать с помощью графика или диаграммы, используя встроенные инструменты Excel.
Обратите внимание, что точность и качество построения плоскости будут зависеть от правильности введенных данных и используемых инструментов Excel.
Определение коэффициентов уравнения плоскости
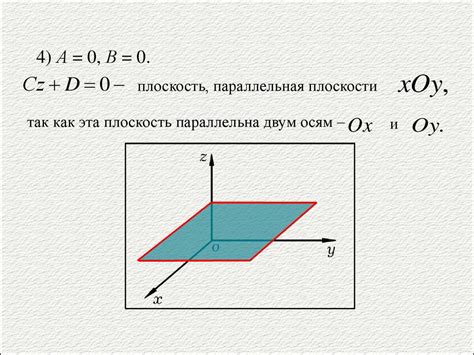
Уравнение плоскости в трехмерном пространстве может быть выражено в виде:
Ax + By + Cz + D = 0
где A, B и C - коэффициенты плоскости, определяющие ее наклон и ориентацию, а D - свободный член.
Чтобы определить значения коэффициентов A, B, C и D, необходимо иметь минимум три точки, принадлежащие плоскости.
Подставляя координаты этих точек в уравнение плоскости, можно составить систему линейных уравнений и решить ее методом подстановки или исключения.
Коэффициенты A, B, C и D получаются из решения системы уравнений, причем коэффициент перед переменной x - это A, перед y - это B, перед z - это C, а свободный член - это D.
Зная коэффициенты уравнения плоскости, можно построить ее в Microsoft Excel, использовав функцию "Замечательная поверхность".
Построение графика плоскости
Построение графика плоскости в программе Excel может быть полезной задачей для визуализации и анализа данных. Для этого можно использовать функцию "Рассеяние", которая позволяет создавать трехмерные графики.
Для начала необходимо иметь уравнение плоскости в виде Ax + By + Cz + D = 0, где A, B, C и D - это заданные коэффициенты. Затем можно перейти к построению графика следующим образом:
- Откройте программу Excel и создайте новый рабочий лист.
- Введите значения коэффициентов A, B, C и D в ячейки выбранного столбца или строки.
- В ячейке, где должен быть график, введите формулу, которая будет описывать уравнение плоскости. Например, если коэффициенты A, B, C и D находятся в ячейках A1, B1, C1 и D1 соответственно, формула может выглядеть так: =A1*x + B1*y + C1*z + D1.
- Для построения "равномерной" плоскости можно создать таблицу значений координат x, y и z. Для этого создайте столбцы или строки с соответствующими значениями и использовать формулу из пункта 3 для подсчета z для каждого значения x и y.
- Выберите ячейки с данными и заголовками, а затем откройте вкладку "Вставка" в верхней панели инструментов. Найдите категорию "Рассеяние" и выберите трехмерный график с подходящим стилем.
- После этого Excel построит график плоскости и выведет его в отдельном окне. В этом окне можно настроить внешний вид графика, добавить подписи осей и многое другое.
Теперь вы знаете, как построить график плоскости в программе Excel. Этот метод можно использовать для визуализации различных математических моделей и данных, связанных с плоскостями. Удачи!
Анализ готового графика плоскости
После построения графика плоскости в Excel, представляется возможность проанализировать полученные результаты и извлечь полезную информацию. Готовый график позволяет визуально представить плоскость и изучить ее основные характеристики.
Первым шагом при анализе графика плоскости является оценка ее ориентации. Заметьте, какие оси координат отображены на графике. Вертикальная ось обозначает одну из переменных, а горизонтальная - другую.
По форме графика можно судить о направлении плоскости и её наклоне относительно осей координат.
По оси координат часто отложены значения переменных плоскости. Значения, приравненные к нулю, обозначают точку пересечения плоскости с этой осью. Также можно рассмотреть значения, при которых график плоскости пересекает другую ось координат.
Следующим шагом при анализе готового графика плоскости является исследование ее формы и кривизны. Определите, является ли график прямой линией или имеет некоторую кривизну. Смотрите, какие точки графика находятся ближе к оси координат, а какие - дальше от нее. Это может помочь определить наклон плоскости и ее линейную или изогнутую форму.
Также обращайте внимание на пересечения линий на графике. Они могут указывать на точки пересечения плоскости с другими плоскостями или осями координат.
Оценивая график плоскости, можно также обращать внимание на preselurl, на котором начинается и заканчивается плоскость. Они могут указывать на область, где плоскость возрастает или убывает, а также на наличие экстремальных значений.