Найти площадь треугольника – одна из базовых задач геометрии, и существует множество способов решения этой задачи. Одним из простых методов нахождения площади треугольника является использование периметра и длины одной из его боковых сторон.
Периметр треугольника равен сумме длин всех его сторон. Поэтому если известен периметр и длина одной из боковых сторон треугольника, то можно легко найти длины остальных сторон, используя свойство равенства сторон треугольника. Зная все стороны треугольника, можно применить формулу Герона для нахождения его площади.
Формула Герона позволяет найти площадь треугольника, используя только длины его сторон. Она представляет собой квадратный корень из произведения полупериметра треугольника и разностей между полупериметром и длинами его сторон. Данный метод позволяет найти площадь треугольника без необходимости знать его высоту или углы.
Способ 1: Формула Герона для нахождения площади треугольника
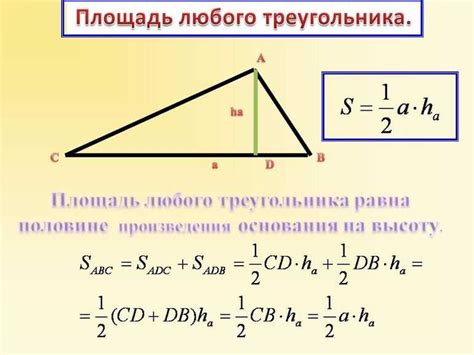
Формула Герона выглядит следующим образом:
| Формула Герона: | |
| Площадь: | S = √(p(p - a)(p - b)(p - c)) |
| где: | |
| площадь | S - площадь треугольника |
| периметр | p - полупериметр (периметр треугольника, деленный на 2) |
| боковые стороны | a, b, c - длины сторон треугольника |
Чтобы найти площадь треугольника по формуле Герона, необходимо:
- Найти полупериметр, вычислив сумму длин всех сторон и разделив ее на 2.
- Используя значения сторон и полупериметра, подставить их в формулу Герона.
- Вычислить квадратный корень из полученного значения.
Пример:
Допустим, у нас есть треугольник со сторонами a = 5, b = 7 и c = 9.
Сначала найдем полупериметр: p = (5 + 7 + 9) / 2 = 10.5
Теперь подставим все значения в формулу Герона: S = √(10.5(10.5 - 5)(10.5 - 7)(10.5 - 9)) = √(10.5 * 5.5 * 3.5 * 1.5) ≈ 19.39
По формуле Герона получаем, что площадь этого треугольника примерно равна 19.39 квадратных единиц.
Таким образом, использование формулы Герона является достаточно простым и эффективным методом нахождения площади треугольника по заданным аргументам. Этот метод особенно полезен, когда известны только значения сторон треугольника и требуется быстрый результат.
Способ 2: Вычисление площади через полупериметр и радиус вписанной окружности

| Формула | Пояснение |
|---|---|
| S = r * p | где S - площадь треугольника, r - радиус вписанной окружности, p - полупериметр треугольника |
Чтобы вычислить площадь треугольника по этому способу, необходимо:
- Найти полупериметр треугольника (p) по известным значениям его сторон.
- Вычислить радиус вписанной окружности (r) с помощью формулы: r = S/p.
- Умножить радиус вписанной окружности (r) на полупериметр треугольника (p) для получения значения площади треугольника (S).
Таким образом, используя второй способ, можно без обращения к высоте треугольника вычислить его площадь, используя только информацию о боковых сторонах.
Способ 3: Использование радиуса вписанной окружности и длины отрезков, проведенных из ее центра к вершинам треугольника

Существует еще один метод нахождения площади треугольника, который основан на использовании радиуса вписанной окружности и длины отрезков, проведенных из ее центра к вершинам треугольника.
Для применения этого метода нужно знать следующие величины: периметр треугольника (P) и длины отрезков (a, b, c), которые соединяют центр вписанной окружности с вершинами треугольника.
Для начала найдем радиус вписанной окружности (r). Радиус можно найти по формуле:
r = P / (2 * s),
где P - периметр треугольника, s - полупериметр треугольника (s = (a + b + c) / 2).
Когда радиус найден, можно рассчитать площадь треугольника (S) по формуле:
S = r * a * b * c / (4 * R),
где R - радиус описанной окружности (R = a * b * c / (4 * S)).
Этот метод может оказаться полезным, когда изначально даны длины отрезков, проведенных из центра вписанной окружности к вершинам треугольника. Он позволяет найти площадь треугольника без использования высоты или углов треугольника.
Способ 4: Формула для вычисления площади треугольника по координатам вершин
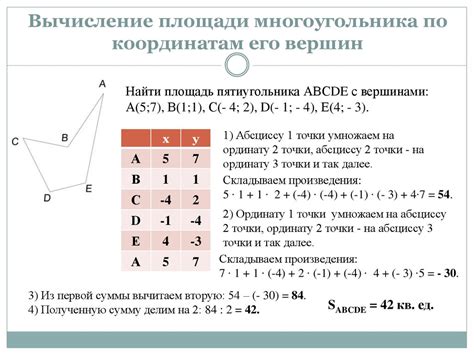
Один из методов вычисления площади треугольника основан на использовании формулы для нахождения площади треугольника по координатам его вершин. Этот метод особенно полезен, когда известны координаты вершин треугольника, но неизвестны длины его сторон.
Для вычисления площади треугольника по координатам вершин необходимо выполнить следующие шаги:
- Находим длины сторон треугольника с помощью формулы расстояния между двумя точками в прямоугольной системе координат.
- Вычисляем полупериметр треугольника по формуле: полупериметр = (сторона 1 + сторона 2 + сторона 3) / 2.
- Используя формулу Герона, находим площадь треугольника: площадь = корень квадратный из (полупериметр * (полупериметр - сторона 1) * (полупериметр - сторона 2) * (полупериметр - сторона 3)).
Этот способ позволяет вычислить площадь треугольника, используя только координаты его вершин. Он может быть полезен в случаях, когда известны только координаты вершин треугольника, но нет информации о его сторонах и углах.
Способ 5: Использование формулы для вычисления площади треугольника по длинам его сторон и рассечении одной стороны на две отрезка в заданном отношении

Если известны длины всех трех сторон треугольника и отношение, в котором одна из сторон рассекается на два отрезка, то площадь треугольника можно найти с помощью следующей формулы:
| Шаги | Формула |
|---|---|
| Шаг 1 | Найдите полупериметр треугольника, который можно вычислить по формуле: полупериметр = (a + b + c) / 2, где a, b и c - длины сторон треугольника. |
| Шаг 2 | Используя отношение d, примените следующие формулы для нахождения длин двух отрезков: d1 = d * a / (1 + d) и d2 = a - d1, где d - заданное отношение, а d1 и d2 - длины отрезков, на которые рассекается сторона a. |
| Шаг 3 | Вычислите площади двух треугольников с боковыми сторонами a, d1 и d2 с помощью формулы Герона: площадь = sqrt(s * (s - a) * (s - d1) * (s - d2)), где s - полупериметр треугольника. Затем сложите полученные площади двух треугольников, чтобы получить итоговую площадь треугольника. |
Используя данный метод, вы легко найдете площадь треугольника, если известны его стороны и отношение рассечения одной из сторон на два отрезка.