Прямоугольный треугольник - это особый вид треугольника, у которого один из углов равен 90 градусам. Относительно этого особого угла можно выделить две стороны треугольника - катеты и одну сторону - гипотенузу.

Катеты - это две стороны прямоугольного треугольника, которые образуют прямой угол. Их длины можно найти с помощью теоремы Пифагора. Теорема Пифагора утверждает, что квадрат длины гипотенузы равен сумме квадратов длин катетов: a² + b² = c².

Таким образом, чтобы найти длину катета, нужно взять квадратный корень от разности квадрата длины гипотенузы и квадрата другого катета. Если известна длина одного катета и гипотенузы, можно найти длину второго катета, применив ту же формулу.

Как найти катет и гипотенузу прямоугольного треугольника

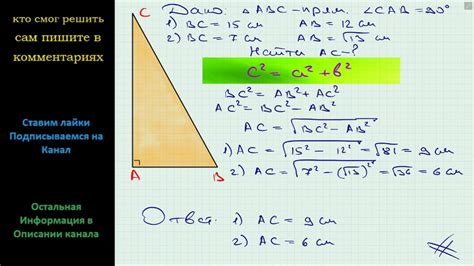
Теорема Пифагора гласит, что квадрат гипотенузы (самая длинная сторона треугольника) равен сумме квадратов катетов (две короткие стороны треугольника):

c^2 = a^2 + b^2

где c - гипотенуза, а a и b - катеты

Если известна гипотенуза и один из катетов, можно найти второй катет. Для этого нужно составить уравнение и решить его:

a^2 = c^2 - b^2

a = sqrt(c^2 - b^2)

где a - искомый катет, c - гипотенуза, b - известный катет

Если известны оба катета, можно найти гипотенузу. Для этого нужно составить уравнение и решить его:

c^2 = a^2 + b^2

c = sqrt(a^2 + b^2)

где c - искомая гипотенуза, a и b - известные катеты

Теперь, когда вы знаете как найти катет и гипотенузу прямоугольного треугольника, вы можете легко выполнять подобные задачи.

Определение и свойства прямоугольного треугольника

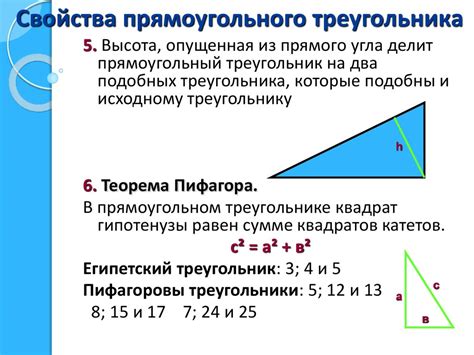
1. Гипотенуза: Гипотенуза – это самая длинная сторона прямоугольного треугольника, которая находится напротив прямого угла. Именно она является диагональю квадрата, построенного на других двух сторонах треугольника.
2. Катеты: Катеты – это две короткие стороны прямоугольного треугольника, которые образуют прямой угол. Они являются основаниями квадрата, построенного на гипотенузе.
3. Формула Пифагора: В прямоугольном треугольнике верна знаменитая формула Пифагора: квадрат гипотенузы равен сумме квадратов катетов. То есть a^2 + b^2 = c^2, где a и b – длины катетов, а c – длина гипотенузы.
4. Третья сторона: Третья сторона прямоугольного треугольника называется острым углом. Его длина может быть найдена с помощью формулы Пифагора, если известны длины двух других сторон.
5. Тригонометрические функции: В прямоугольном треугольнике можно использовать тригонометрические функции для вычисления углов и сторон. Например, синус угла равен отношению длины противоположенного катета к длине гипотенузы.

Зная свойства прямоугольного треугольника, можно легко найти длины его сторон и углы, а также использовать их для решения различных задач и задач геометрии.