Нахождение катета треугольника по известной гипотенузе является одним из основных заданий в геометрии. Этот процесс может показаться сложным, особенно для начинающих, однако существует простая формула, которая позволяет решить эту задачу с минимальными усилиями.
Для начала нужно понять, что такое гипотенуза и катет. Гипотенуза - это самая длинная сторона треугольника, которая расположена напротив прямого угла. Катеты - две оставшиеся стороны треугольника, которые попадают на прямой угол. Иногда требуется найти длину одного из катетов, если известна гипотенуза и другой катет.
Для нахождения катета треугольника по гипотенузе можно использовать теорему Пифагора. Согласно этой теореме, сумма квадратов катетов треугольника равна квадрату гипотенузы. Таким образом, формула для нахождения катета выглядит следующим образом: a = √(c^2 - b^2), где a - катет, c - гипотенуза, b - другой катет.
Пример расчета. Предположим, что у нас есть треугольник, у которого гипотенуза c = 5 и катет b = 3. Чтобы найти катет a, подставим значения в формулу a = √(5^2 - 3^2). Раскроем скобки и пересчитаем: a = √(25 - 9), a = √16, a = 4. Таким образом, длина катета a равна 4.
Определение катета треугольника
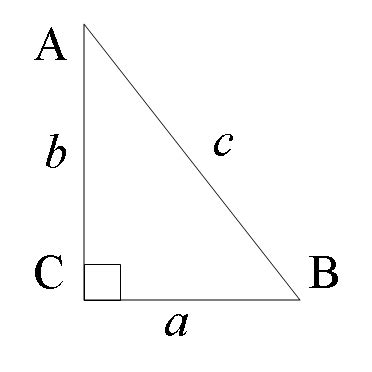
Катетом называется одна из сторон прямоугольного треугольника, которая состоит из двух перпендикулярных друг другу сторон. В прямоугольном треугольнике катеты всегда смежны с прямым углом.
Определить значение катета треугольника можно, зная длину гипотенузы и другого катета. Для этого можно использовать формулу Пифагора:
a2 + b2 = c2
Где:
- a и b - катеты треугольника;
- c - гипотенуза треугольника.
Из формулы Пифагора можно выразить значение катета:
a = √(c2 - b2)
Таким образом, если известны длина гипотенузы и одного из катетов, можно легко найти значение другого катета треугольника.
Какие бывают стороны треугольника
В треугольнике можно выделить три различные стороны: гипотенузу, катеты и, возможно, биссектрису.
Гипотенуза - это самая длинная сторона треугольника, противоположная прямому углу. Если треугольник не является прямоугольным, то гипотенуза отсутствует.
Катеты - это две стороны, образующие прямой угол с гипотенузой. Катеты могут быть разной длины и могут быть равными между собой.
Биссектриса - это отрезок, перпендикулярный одной из сторон треугольника и равномерно делящий противолежащий угол на две равные части. Биссектриса может быть равна одной из сторон треугольника или меньше или больше ее длины.
| Сторона | Описание |
|---|---|
| Гипотенуза | Самая длинная сторона, противоположная прямому углу |
| Катеты | Две стороны, образующие прямой угол с гипотенузой |
| Биссектриса | Отрезок, перпендикулярный одной из сторон треугольника и равномерно делящий противолежащий угол на две равные части |
Зная тип треугольника и значения сторон, можно производить различные расчеты и измерения, включая нахождение катета треугольника по гипотенузе.
Связь между сторонами треугольника
В геометрии существует связь между сторонами треугольника, которая называется теоремой Пифагора. Она утверждает, что квадрат гипотенузы треугольника равен сумме квадратов катетов.
Для нахождения катета треугольника по известной гипотенузе, мы можем использовать эту теорему. Если известна гипотенуза и один из катетов, мы можем решить уравнение и найти второй катет.
Допустим, у нас есть прямоугольный треугольник со сторонами a, b и c, где c - гипотенуза, а a и b - катеты. Тогда согласно теореме Пифагора, выполняется уравнение:
c^2 = a^2 + b^2
Если известны значения гипотенузы и одного из катетов, мы можем подставить их в формулу и решить уравнение, чтобы найти второй катет.
Например, если у нас есть треугольник со сторонами c = 5 и a = 3, мы можем использовать уравнение:
5^2 = 3^2 + b^2
25 = 9 + b^2
b^2 = 16
b = 4
Таким образом, второй катет треугольника равен 4.
Нахождение катета треугольника по гипотенузе
Для нахождения катета треугольника по гипотенузе используется теорема Пифагора, которая утверждает, что квадрат гипотенузы равен сумме квадратов катетов. Таким образом, чтобы найти длину катета, необходимо из квадрата длины гипотенузы вычесть квадрат длины известного катета и извлечь квадратный корень из полученного значения.
Формула для нахождения катета треугольника по гипотенузе:
c = sqrt(a^2 - b^2)
Где:
- c - длина катета;
- a - длина гипотенузы;
- b - длина известного катета.
Применим данную формулу на практике. Предположим, что известна длина гипотенузы треугольника, которая равна 10, а также известна длина одного из катетов, которая равна 6. Чтобы найти длину второго катета, следует подставить значения в формулу:
c = sqrt(10^2 - 6^2)
c = sqrt(100 - 36)
c = sqrt(64)
c = 8
Таким образом, длина второго катета треугольника равна 8.
Зная формулу и метод ее применения, можно легко находить длину катета треугольника по известным значениям гипотенузы и другого катета.
Формула для расчета катета

Для нахождения значения катета треугольника, если известна длина гипотенузы, существует простая формула.
Пусть a - длина катета, а c - длина гипотенузы.
Тогда с использованием Пифагоровой теоремы мы можем записать следующее уравнение:
a2 + b2 = c2
Рассмотрим случай, когда мы знаем длину гипотенузы и один из катетов, а хотим найти длину другого катета. Пусть известно, что a = 3 и c = 5.
Подставим эти значения в уравнение:
32 + b2 = 52
9 + b2 = 25
b2 = 25 - 9
b2 = 16
b = 4
Таким образом, значение второго катета равно 4.
Примеры расчетов

Рассмотрим несколько примеров расчета катета треугольника по заданной гипотенузе:
- Пусть гипотенуза равна 10 см. Используя формулу катета треугольника, найдем значение одного из катетов:
a = √(с² - b²) = √(10² - b²) - Пусть гипотенуза равна 15 см. Найдем значение другого катета:
- Если нам дано значение гипотенузы и одного из катетов, можно использовать ту же формулу для нахождения второго катета:
Пусть b = 8 см, тогда:
a = √(10² - 8²) = √(100 - 64) = √36 = 6 см
a = √(с² - b²) = √(15² - b²)
Пусть b = 9 см, тогда:
a = √(15² - 9²) = √(225 - 81) = √144 = 12 см
b = √(с² - a²) = √(13² - a²)
Пусть a = 5 см, тогда:
b = √(13² - 5²) = √(169 - 25) = √144 = 12 см
Таким образом, используя простую формулу катета треугольника по гипотенузе, можно легко находить значения катетов и решать различные геометрические задачи.
Применение определения катета треугольника
Для этого нам понадобится использовать теорему Пифагора, которая гласит: квадрат длины гипотенузы равен сумме квадратов длин катетов. Из этой формулы можно выразить один из катетов, подставив известные значения в уравнение и решив его.
Применение определения катета треугольника может быть полезно при решении различных геометрических задач, например, при нахождении размеров прямоугольного участка земли или при расчете длинной диагонали прямоугольника.
Также определение катета применяется в различных областях науки и техники, например, в архитектуре, строительстве, электронике и других сферах, где требуется проводить точные измерения и расчеты.