Наверняка каждый из нас сталкивался с ситуацией, когда нужно было решить геометрическую задачу без использования специальных инструментов. Например, определить значение тангенса угла. В этой статье мы расскажем вам о простом способе, который позволяет найти тангенс угла всего лишь с помощью клетчатой бумаги.
Для начала, возьмите кусок клетчатой бумаги и нарисуйте на ней прямоугольный треугольник с известным вам углом. Убедитесь, что одна из сторон треугольника лежит по одной из горизонтальных линий клеток, а другая сторона - по одной из вертикальных линий.
Затем, измерьте длину горизонтальной стороны треугольника с помощью клетчатой бумаги. Подсчитайте количество клеток, которое занимает данная сторона. Это будет ваша опорная величина. Обозначим ее как "a".
Далее, измерьте длину вертикальной стороны треугольника также с помощью клетчатой бумаги. Подсчитайте количество клеток, которое занимает эта сторона. Обозначим ее как "b".
Наконец, чтобы найти тангенс угла, поделите значение "b" на значение "a". Полученный результат и будет тангенсом искомого угла. Не забудьте округлить ответ до нужного количества знаков после запятой, если требуется.
Что такое тангенс и зачем он нужен?

Главное назначение тангенса заключается в его способности измерять углы. Действительно, имея значение тангенса угла, мы можем точно определить, насколько этот угол крут или крутится из исходного положения. Кроме того, тангенс может использоваться для нахождения высоты или расстояния до объекта, если известно расстояние до этого объекта и угол, под которым его видно.
Формула нахождения тангенса угла:
тангенс угла = противолежащий катет / прилежащий катет
Тангенс также является базовой функцией для вычисления других важных тригонометрических функций, таких как синус и косинус. Поэтому понимание тангенса является ключевым фактором для работы с тригонометрическими выражениями и задачами.
Как работает тангенс на клетчатой бумаге?

Для начала нарисуем на клетчатой бумаге прямоугольный треугольник, в котором известны прилежащая сторона и противоположная сторона угла, тангенс которого мы хотим найти. Нарисуем прилежащую сторону горизонтально, а противоположную сторону - под углом.
Посмотрим на клетки, по которым проходит противоположная сторона. Проведем линию через каждую клетку, через которую проходит противоположная сторона, и затем продолжим линию до конца клетчатой бумаги или другого ориентира.
Теперь нам нужно найти количество клеток, через которые проходит прилежащая сторона. Проведем линию через каждую клетку, через которую проходит прилежащая сторона, и затем продолжим линию до конца клетчатой бумаги или другого ориентира.
Найдем отношение количества клеток на линии противоположной стороны к количеству клеток на линии прилежащей стороны. Полученное значение и будет тангенсом угла.
Важно помнить, что тангенс может быть положительным или отрицательным в зависимости от положения противоположной стороны относительно прилежащей стороны. Также следует учесть, что клетки на бумаге должны быть одинакового размера, чтобы получить точный результат.
Теперь, когда вы знаете, как работает тангенс на клетчатой бумаге, вы можете легко находить значения этой функции угла без использования сложных математических формул.
Почему использование клетчатой бумаги для расчета тангенса угла?

- Визуальное представление углов: Клетчатая бумага позволяет наглядно представить угол и его изменение при расчете тангенса. Каждая клеточка на бумаге представляет собой угол в 45 градусов, что облегчает понимание расчетов.
- Точность расчетов: Благодаря наличию сетки из клеточек на бумаге, можно легко измерить длину катетов треугольника и определить отношение между ними, не ошибаясь в измерениях и соответственно в расчетах тангенса.
- Простота использования: Расчеты на клетчатой бумаге требуют лишь базовых математических навыков и знания формулы тангенса. Достаточно провести пару прямых линий и выполнить простые вычисления, чтобы получить значение тангенса угла.
- Универсальность: Клетчатую бумагу легко найти или создать самостоятельно, что делает ее доступным и удобным инструментом для расчетов тангенса угла в любом месте и в любое время.
В итоге, использование клетчатой бумаги для расчета тангенса угла позволяет упростить и ускорить процесс вычислений, а также повысить точность результатов.
Как найти тангенс угла на клетчатой бумаге без калькулятора?

Определение тангенса угла без использования калькулятора может быть произведено на клетчатой бумаге с помощью оценки соотношения длин сторон прямоугольного треугольника. Для этого следует выполнить следующие шаги:
- Нарисуйте на клетчатой бумаге прямоугольный треугольник с известным углом.
- Измерьте длину катета, соответствующего углу, на количестве клеток.
- Измерьте длину прилежащего катета на том же количестве клеток.
- Рассчитайте отношение длины противоположнего катета к длине прилежащего катета.
- Это отношение будет приближенным значением тангенса угла.
Например, если длина противоположнего катета равна 5 клеток, а длина прилежащего катета равна 3 клеткам, то тангенс угла будет примерно равен 5/3.
Этот метод может быть полезен для оценки тангенса угла без использования калькулятора, и он также помогает развить интуитивное понимание тригонометрических функций.
Полезные советы для точного определения тангенса на клетчатой бумаге
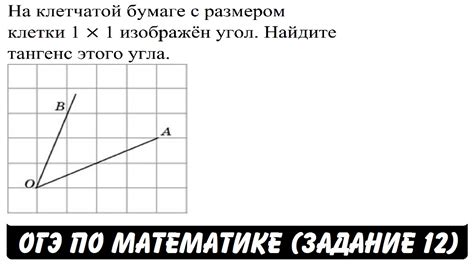
Вот полезные советы, которые помогут вам опеределить тангенс угла на клетчатой бумаге:
- Начните с выбора угла, для которого вы хотите определить тангенс.
- Нарисуйте прямую линию, представляющую основание угла, на клетчатой бумаге. Эта линия будет соединять начало и конец угла.
- От начала основания угла отметьте точку на нижней или верхней границе клеточки. Это поможет вам определить длину противоположной стороны угла.
- Измерьте длину противоположной стороны с помощью клеток на клетчатой бумаге и запишите это значение.
- Затем измерьте длину прилежащей стороны, считая количество клеток, которые она занимает.
- Тангенс угла будет равен отношению длины противоположной стороны к длине прилежащей стороны.
Таким образом, вы можете использовать клетчатую бумагу для определения точного значения тангенса угла. Важно следовать указанным шагам и быть внимательным при измерении, чтобы получить верный результат.
| Угол (в градусах) | Противоположная сторона | Прилежащая сторона | Тангенс |
|---|---|---|---|
| 30 | 1 клетка | √3 клетки | √3/1 = √3 |
| 45 | 1 клетка | 1 клетка | 1/1 = 1 |
| 60 | √3 клетки | 1 клетка | √3/1 = √3 |
С помощью этих советов и таблицы тангенсов вы сможете точно определить тангенс угла на клетчатой бумаге и применять его в своих расчетах.
Практическое применение нахождения тангенса угла на клетчатой бумаге
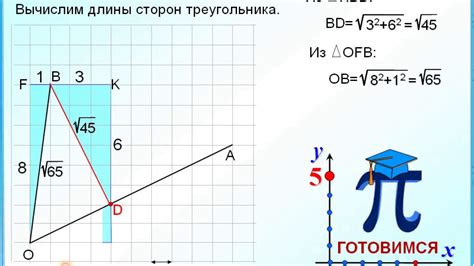
Нахождение тангенса угла на клетчатой бумаге имеет практическое применение в различных областях, включая геометрию, строительство, архитектуру и физику. С помощью такого метода можно быстро и относительно точно определить значение тангенса угла без использования сложных математических вычислений или специального оборудования.
Примером практического применения может быть измерение высоты объекта на расстоянии с помощью тангенса угла. Для этого необходимо измерить длину отрезка на бумаге, соединяющего наблюдателя и верхушку объекта, и поделить его на количество клеток между этими точками. Затем, используя таблицу тангенсов, можно найти значение тангенса угла и вычислить высоту объекта с помощью простой формулы.
| Угол (градусы) | Тангенс угла |
|---|---|
| 0 | 0 |
| 15 | 0.27 |
| 30 | 0.58 |
| 45 | 1 |
| 60 | 1.73 |
| 75 | 3.73 |
| 90 | неопределенность |
Другим примером может быть определение длины тени объекта на солнечных часах. Измерив длину отрезка на бумаге, соединяющего объект и конец его тени, и зная расстояние до объекта, можно применить тангенс угла и вычислить длину тени. Этот метод может использоваться для определения времени дня на основе длины тени и известной высоты объекта, например, в садоводстве или навигации.