Углы треугольника - это одна из главных составляющих его геометрической структуры. Знание углов помогает в решении различных задач и вычислении других параметров треугольника. И хотя существуют формулы для нахождения углов, существует и более простой способ.
Если вам необходимо определить угол треугольника, но вы не хотите заморачиваться с использованием формул, вы можете воспользоваться основным свойством треугольника, а именно суммой углов внутри треугольника. Согласно этому свойству, сумма всех внутренних углов треугольника всегда равна 180 градусам. Исходя из этого, можно легко вычислить отсутствующий угол, зная значения остальных углов.
Допустим, у вас есть треугольник, в котором известны значения двух углов. Чтобы найти третий угол, достаточно вычесть сумму известных углов из 180 градусов. Полученное значение будет являться значением отсутствующего угла.
Таким образом, нахождение угла треугольника без использования формулы оказывается довольно простым и эффективным. Этот метод может быть особенно удобен в решении геометрических задач на экспресс-уроках или в быстром повседневном расчете. Отличительной особенностью данного метода является его интуитивность и доступность для понимания без специальных математических знаний.
Определение угла треугольника
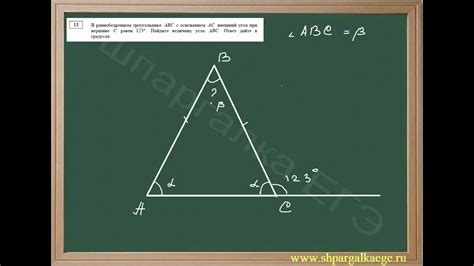
Существует несколько способов определения угла треугольника:
- Использование транспортира. Транспортир - это инструмент, который используется для измерения углов. Он представляет собой полукруглую шкалу с делениями от 0 до 180 градусов. Чтобы определить угол треугольника с помощью транспортира, необходимо положить его на вершину угла так, чтобы одна из его линий проходила по одной из сторон треугольника. Затем следует определить, на каком значении шкалы останавливается вторая линия транспортира, и это будет значение угла.
- Использование геометрических формул. Углы треугольника связаны между собой формулами и правилами геометрии. Например, сумма углов треугольника всегда равна 180 градусам. Если известны значения двух углов треугольника, можно найти значение третьего угла, вычитая из 180 градусов сумму известных углов.
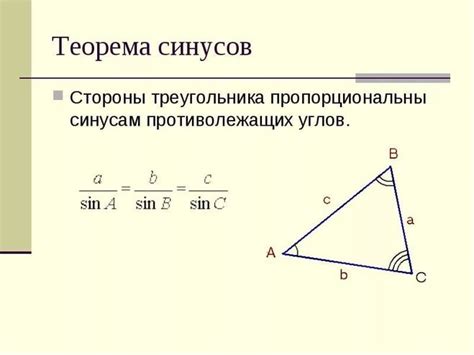
- Использование геометрических свойств треугольников. Например, если треугольник является прямоугольным, то один из его углов будет равен 90 градусам. Также можно использовать соотношения между сторонами и углами треугольника, такие как теорема синусов или теорема косинусов, для определения углов.
Определение угла треугольника может быть полезным навыком при решении различных задач в геометрии и углометрии. Знание основных методов определения угла треугольника позволяет более точно изучать геометрические фигуры и выполнять решение задач, связанных с треугольниками.
Угол треугольника: что это такое?
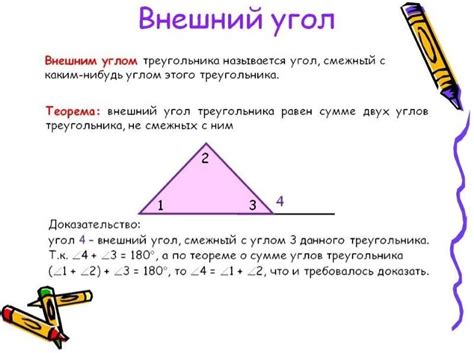
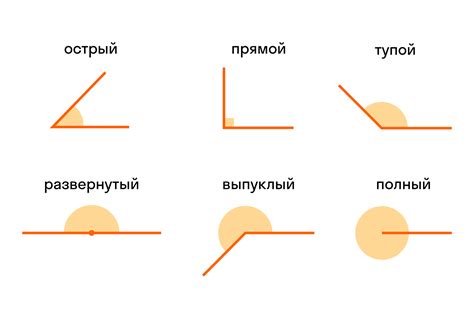
Углы треугольника могут быть различными по своей величине и положению. Они могут быть острыми (меньше 90 градусов), прямыми (равны 90 градусов) или тупыми (больше 90 градусов).
Углы треугольника имеют важное значение при решении геометрических задач. Зная значения двух углов треугольника, можно вычислить третий угол, используя свойство их суммы. Это позволяет решать задачи на нахождение неизвестных углов в треугольниках.
Существуют различные методы для измерения углов треугольника, включая использование транспортира или применение геометрических формул. Однако, существуют и простые способы приближенно определить угол треугольника без использования сложных инструментов или формул.
Зачем нужно знать угол треугольника?
1. Измерение и конструирование Зная значения углов треугольника, мы можем измерять и конструировать объекты на основе их геометрических свойств. Например, при строительстве зданий и мостов, знание углов позволяет правильно расположить балки и стержни. | 2. Решение геометрических задач Решение геометрических задач часто требует определения углов треугольников. Это может быть полезно при работе с картами, изучении геодезии или даже при игре в пул. |
3. Построение планов растворов В химии, знание углов треугольника может понадобиться для определения объемов и концентраций растворов. Это особенно важно при подготовке лекарственных препаратов или в лабораторных исследованиях. | 4. Планирование маршрутов и навигация При планировании маршрутов в географии или вождении автомобиля, знание углов треугольника позволяет определить направление и расстояние между точками. |
Все эти примеры подчеркивают важность знания углов треугольника без использования сложных формул. Они позволяют применить геометрические принципы в различных сферах деятельности, улучшая качество работы и повышая точность результатов.
Простой способ измерить угол треугольника
Измерение угла треугольника может показаться сложной задачей, особенно если у вас нет специального инструмента или рулетки. Однако, существует простой способ определить угол без использования формул и сложных вычислений.
Вам понадобится только ручка, бумага и линейка. Вот как это сделать:
- Нарисуйте треугольник на бумаге, включая все три стороны.
- Выберите одну из сторон треугольника и обозначьте ее как "основание".
- Возьмите линейку и расположите ее вдоль основания треугольника.
- Смотря на линейку и фиксируя одним глазом, определите, где пересекается другая сторона треугольника с линейкой.
- Считайте количество делений или сантиметров от начала линейки до точки пересечения стороны треугольника. Это будет вашим измерением.
Теперь вы можете использовать измерение для определения угла треугольника без использования формулы. Просто найдите значения двух других сторон треугольника и примените их к теореме косинусов или теореме синусов, чтобы найти угол.
Этот простой метод может быть очень полезным, особенно когда вы находитесь в ситуации, где необходимо быстро и точно измерить угол треугольника, но у вас нет доступа к инструментам или сложным формулам.
Шаг 1: Измерить два известных угла
Первым шагом необходимо измерить два известных угла треугольника. Для этого можно воспользоваться угломером или простым геодезическим инструментом. Сначала выберите одну из сторон, которую вы считаете базовой стороной треугольника, и измерьте угол, образованный этой стороной и следующей стороной треугольника.
Затем выберите другую сторону и измерьте угол, образованный этой стороной и предыдущей стороной треугольника. Оба измеренных угла будут известными углами треугольника, и они помогут в дальнейших расчетах.
Примечание: Углы треугольника суммируются в сумму 180 градусов. Поэтому сумма измеренных углов должна быть равна 180 градусов. Если сумма измеренных углов не равна 180 градусов, значит, либо измерения были неточными, либо треугольник не является обычным треугольником.
Шаг 2: Измерить длину третьей стороны
После того как вы измерили длину двух сторон треугольника, осталось узнать длину третьей стороны. Для этого вы можете воспользоваться линейкой или мерной лентой.
Проведите линейку или мерную ленту вдоль третьей стороны треугольника, начиная от одного из углов. Запишите полученное значение длины третьей стороны.
Если у вас нет линейки или мерной ленты, вы можете воспользоваться другими предметами для измерения. Например, вы можете использовать лист бумаги или школьные тетради с известной шириной, чтобы приблизительно измерить длину третьей стороны треугольника.
Шаг 3: Применить теорему косинусов
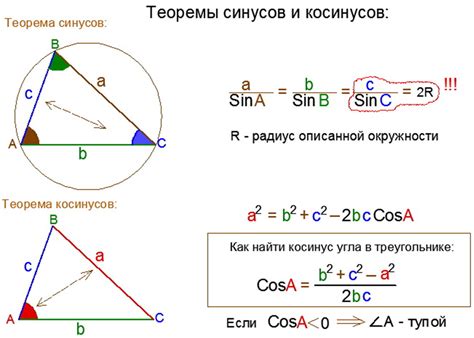
Чтобы узнать угол треугольника без использования формулы, мы можем использовать теорему косинусов. Эта теорема позволяет нам вычислить угол, если известны длины всех трех сторон треугольника.
Формула для теоремы косинусов выглядит следующим образом:
c2 = a2 + b2 - 2ab * cos(C)
Где c - длина стороны треугольника противоположной углу C, a и b - длины двух других сторон треугольника, а C - искомый угол.
Применяя эту формулу, мы можем вычислить искомый угол, зная длины всех трех сторон треугольника.
Таким образом, применяя теорему косинусов, мы можем узнать угол треугольника без использования формулы.